Behavioral Business Strategy Development For Economic Industrial Entities Using Fuzzy Set Theory

Abstract

The economic development of Eastern Siberea is one of the priorities of the Russian government. The efficient development of business strategies in economics aims to ensure a growing regional product due to satisfaction of workers with working conditions and development of raw material resources. The present study analyzes possibilities of economic activization due to its balanced development using efficient programs of economic growth incoprporating all possibilities of the current economic state of large businesses and calculation of risk aversion using the fuzzy set theory. The method for business strategy development takes into account the synergy of business and territory development needs. Under a restricted admissible market balance, the method is reasonable. The model improves efficiency of business resource management. An integral index gives an idea of the use of resources in terms of their availability and allows controlling their efficient development. If resources are limited, additional ones can be used The method for assessing general education resources using the fuzzy set theory gives quantitative estimation of regional general education resources; identifies causes of the imbalance of the education system. Management and labor resources are at the top level of the hierarchy while financial, material and technical and information resources are at the low level.

Keywords: Development strategyprograms of strategic and tactic interaction of economic activitiesfuzzy set theory and its application to the strategic planning

Introduction

An investment component is getting more important in the economy. However, researches on investment activities do not provide an adequate methodological approach to the issue. There are no developed and implemented programs of strategic and tactic relations of economic components, and theoretical approaches to development of a system-oriented strategy of business process activation.

Economic and mathematical simulation can solve these problems based on a compromise and concession method. It helps identify cause and effect relations between resource requirements and efficient resource management. However, many crucial economic situations with complex goals and restrictions are ignored as they cannot be interpreted from a mathematical perspective. To solve these problems, it is necessary to stop complying with accuracy requirements and start interpreting ambiguous or uncertain results (Zhukovin, 1986) A number of publications dedicated to different aspects of the fuzzy set theory (linear programming with fuzzy coefficients, fuzzy mathematical programming with accurate goals, fuzzy Pareto set solution, etc.) are increasing (Orlivsky, 1981).

The present study applies two methods. The first one is based on the membership function introduced by Zadeh (1973). The second method is based on quantitative description of fuzzy situations by using numerical information instead of non-numerical and applying decision theory tools

Problem Statement

Production functions, which can be used to predict and control economic behavior dynamics, are a promising field in developing of a system-oriented economic decision-making strategy. These regularities can identify the system of relations of social and economic development levels for territories of business subjects.

The rational choice theory solves these problems using a method of costs and profits. Government authorities, businesses and other members of the society are driven by their own interests following fuzzy game rules. The first ones follow communication and coordination rules, the second ones – voting system rules. However, the reality is uncertain, and efforts to increase certainty in obtaining desirable advantages can exceed the size of preferences. Players evaluate real risks and possible benefits.

From a decision-making perspective, the system of values is based on facts and assumptions. It can help choose a right decision. De facto, players being unable to collect enough information, instead of searching for an optimum decision, choose any suitable alternative relying on their own system of values. There are also some other methods: the utility theory, costs – performance, costs – benefits. The latter is used to justify a decision already made as far as implicit factors, which can be taken into account, play an important role in this process (Cengiz Toklu, Erdem, & Taşkın, 2016).

A real options method applied for assessing target programs, investment projects, and company assets can eliminate many drawbacks of the current methods used for developing plans and generating predictions. Solutions of optimization tasks are threshold values of these parameters which allow optimum management under uncertainty. The use of the method is described in (Kofman, 1982). Regional governments use target programs to develop industries provided that the real value of an expected money flow derived from the implementation of priority measures of the target program exceeds initial investment resources. Otherwise, the regional government can postpone its implementation. In our example, an analysis of the target program identified results when an estimated option price should be paid now to fulfill provisions of the option contract for textile industry development.

When managing multifactorial economic processes under uncertainty of critical situations, a multicriteria decision making is a useful tool to search for and justify solutions. It is commonly believed that a fuzzy situation occurs under conditions whose causes and elimination strategies are known, but at least one criterion has no quantitative estimate. Under uncertainty, rules and procedures of the fuzzy set theory are particularly topical. The theory is analyzed in a great number of works

Research Questions

In a fuzzy situation, causes are known but not eliminated. Information is verbally described. For example, performance of this process is worse than performance of the previous one, but there are no comparison methods and criteria. The fuzzy set theory gives a decision.

L. Zadeh introduced concepts used by the theory when developing decision making procedures under uncertainty using decision making and fuzzy algorithms tables: linguistic variables, fuzzy sets, fuzzy relations, fuzzy algorithms. A linguistic variable is a variable whose values are words or sentences of a natural or artificial language. For example, “situation” is a linguistic variable whose values are words <normal>, <critical> or characteristics describing conditions and states of business processes <inadequate funding>, <low education quality>, etc.). Fuzzy relations are conditional sentences <if funding is inadequate, output of products evaluated above the average score is small>.

Decision making tables (DMT) are tools of compact presentation of logical rules used to choose actions which should be performed according to decision making conditions and procedures.

A DMT describes four parts (factors, conditions, actions and recommendations).

See Full Size >

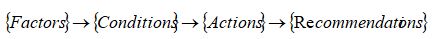
The tables determine which conditions should be taken into account before taking this or that action, which recommendations should be suggested to eliminate the situation, and give information to assess the efficiency of the decision made. The degree of membership is expressed with modifiers added to a linguistic variable value.

Purpose of the Study

The use of DMTs for fast elimination of fuzzy situations differs from traditional enlarging analysis area control using descriptive operations of linguistic variables and control instruction operations in which a number of instructions–actions in the form of typical or non-typical recommendations (fuzzy algorithms - instructions) are issued (Saati, 1993).

The decision-making algorithm for a situation control method involves four stages:

• Situation assessment using numerical and nonnumerical information and identification of its criticality level for making alternative decisions.

• Development of a set of criteria based on the results of macro- and micro-situation analysis. Identification and description of restrictions to cause and effect relations and admissible deviation levels by each micro-situation. Description of alternative conditions and resources which determine a decision-making strategy.

• Development of determinant rules for decision-making using multicriteria decision-making and fuzzy algorithm methods.

• Providing of situation elimination recommendations in the form of regulating impacts calculated on the basis of objective and subjective models (Zakharov, Bovkun & Vasiliev, 2017).

There are two decision-making procedures: integral (a decision is made based on the whole situation without assessing criteria and resources) and criteria expert (a decision is made by a group of experts and managers analyzing the effects of factors on a final result). An integral decision-making method can be based on the following schemes «assessment of an alternative → providing of recommendations» and «assessment of an alternative → generation of a set of alternatives → providing of recommendations». Using such recommendations, one can determine conditions for optimum strategies; the value of each step in the strategic plan of fast problem situation elimination; rules for eliminating the impacts on the production process. These conditions were used when developing determinant rules for searching for, justifying and making decisions in manufacturing situations based on a graphic model.

For example, decision making rules to eliminate causes of non-fulfillment of a condition can be presented as a dependence on the nature of situation fuzziness.

1.Normal conditions. ${В}_{ф}^{б}={\sum }_{i=1}^n{В}_{фi}^{р}$where ${В}_{ф}^{б}$ – daily output of all workers; ${В}_{фi}^{р}$ – daily output of worker $i$; п – number of workers. Fulfillment of the condition stabilizes the common task and does not require situation control. Eventually, reserves $P_{б}$ of common task over-fulfillment are built up.

2.Situation identification and restriction development rules. If one of the workers fails to fulfill his or her part, the common task can remain unfulfilled. The situation is threatening, when the volume of unfulfilled output $\sum {\Delta }_{ij}$ is equal to the reserve volume. The situation is pre-alarming when the volume of unfulfilled output $\sum {\Delta }_{ij}$ exceeds the reserve volume. In this case, random nonfulfillment of the common task occurs. The situation is alarming when all workers fail to fulfil the task due to causes which are difficult to eliminate.

3.Determinant rules for decision-making are designed to eliminate unacceptable situations. Assessing alternatives, strategies for searching for, justifying and making decisions are identified. Determinant rules should be formalized. To develop their model, a membership function by linguistic variable <low> was used. ${Р}_{б}$ depends on the membership function and an alternative preference function (interference and non-interference in the control process). The decision about the type of interference is based on the maximum preference depending on the subjective probability and ${Р}_{б}$. Traditional tables of conditions and actions are used, but interference recommendations are issued as a fuzzy algorithm. For example, in case of failure to fulfil a task on any day when there is accumulative numerical information about the output, the decision-making strategy is executed in accordance with the above-described procedures (Cayir Ervural, Zaim, Demirel, Aydin, & Delen, 2018).

To solve urgent problems of the Russian economy, it is recommended to use significant financial resources. However, even if they are sufficient and spent when due, underdeveloped management and labor resources and legislation prevent from achieving target results. By assessing relations of components of regional general education system resources, the present study will assume that efficient strategy execution is a reasonable interaction of management, labor, financial, legal, material and technical and information resources.

As far as components have different sizes, and some of them are fuzzy, the use of the fuzzy set theory to assess the state and potential of resources is reasonable

Research Methods

The method for assessing general education resources using the fuzzy set theory gives quantitative estimation of regional general education resources; identifies causes of the imbalance of the education system; assesses impacts of each component on education resources; identifies promising management decision-making areas. The results obtained are as follows.

Management and labor resources are at the top level of the hierarchy while financial, material and technical and information resources are at the low level. Legal resources are a linking component.

That distribution is rather logical as financial, material and technical and information resources are a basis of education economy development. Career education plays an important role. Thus, developed management and labor components are crucial for the efficiency of an education institution. The legal component, which is a set of rights, responsibilities and obligations, connects upper and lower levels.

It should be noted that for elements х from universal and carrier set Е, there is no single-valued answer «high» or «low» for property R. Subset А of universal set E is defined as a set of ranked couples with characteristic membership function µА(х), having values in arranged set М (for example, М=[0,1]). The membership function shows the degree of membership of element х in subset А.

The method also involves reduction of the components of the regional resource subsystem to one size and conclusion about the state and value of regional education resources (Samarukha & Skorobogatova, 2009)

The important elements of the assessment model are as follows: an assessment scheme including development of indices, criteria and restrictions; information extracting and processing methods, including a hierarchy of criteria, estimates, expertise; decision-making methods. The elements of the fuzzy set theory allow decision making based on a fuzzy relation knowledge presentation model. It becomes possible to choose an optimum for the regional education system.

The model is based on the assumption that if $\mathrm{{\rm X}}=\left\{{\mathrm{{\rm X}}}_1,{\mathrm{{\rm X}}}_2,\dots ,{\mathrm{{\rm X}}}_{\mathrm{n}}\right\}=\left\{{\mathrm{{\rm X}}}_1,\mathrm{i}=\mathrm{}\stackrel{-}{1,\mathrm{n}}\right\}$ is a set of alternatives to be assessed and ranked, and $\mathrm{{\rm K}}=\left\{{\mathrm{{\rm K}}}_1,{\mathrm{{\rm K}}}_2,\dots ,{\mathrm{{\rm K}}}_{\mathrm{m}}\right\}=\left\{{\mathrm{{\rm K}}}_{\mathrm{j}},\mathrm{j}=\mathrm{}\stackrel{-}{1,\mathrm{m}}\right\}$ is a set of criteria characterizing alternatives, the degree of satisfaction of alternative ${\mathrm{{\rm X}}}_i$ to criteria ${\mathrm{{\rm K}}}_j$ is membership function ${\phi }_{{\mathrm{k}}_{\mathrm{j}}}\left({\mathrm{{\rm X}}}_{\mathrm{i}}\right)\to \left[\mathrm{0,1}\right]$ . Let $\mathrm{{\rm X}}=\left\{{\mathrm{{\rm X}}}_1,{\mathrm{{\rm X}}}_2,\dots ,{\mathrm{{\rm X}}}_{\mathrm{n}}\right\}=\left\{{\mathrm{{\rm X}}}_1,\mathrm{i}=\mathrm{}\stackrel{-}{1,\mathrm{n}}\right\}$ be a set of elements of education resources which are characterized by a set of unequal criteria $\mathrm{{\rm K}}=\left\{{\mathrm{{\rm K}}}_1,{\mathrm{{\rm K}}}_2,\dots ,{\mathrm{{\rm K}}}_{\mathrm{m}}\right\}=\left\{{\mathrm{{\rm K}}}_{\mathrm{j}},\mathrm{j}=\mathrm{}\stackrel{-}{1,\mathrm{m}}\right\}$, each of which ${\mathrm{K}}_{\mathrm{j}}$ , being a member of the set, is characterized by a subset of private criteria $\mathrm{{\rm K}}=\left\{{\mathrm{{\rm K}}}_{\mathrm{j}1},{\mathrm{{\rm K}}}_{\mathrm{j}2},\dots ,{\mathrm{{\rm K}}}_{\mathrm{j}\mathrm{T}}\right\}=\left\{{\mathrm{{\rm K}}}_{\mathrm{j}\mathrm{t}},\mathrm{t}=\mathrm{}\stackrel{-}{1,\mathrm{T}}\right\}$.

The task is to make systematized conclusions about the impact of each element on the state of the object under study. Elements are ranked from worst to best: $\mathrm{{\rm X}}:\mathrm{{\rm K}}\to {\mathrm{{\rm X}}}^{*}$ where Х* - systematized estimates of resource potential elements (Samarukha & Skorobogatova, 2009).

The assessment algorithm involves the following stages:

1. Having aggregated the private criteria of the lower level, each of them should be assessed at the high level, i.e. it is necessary to denote membership $\left\{{\phi }_{{\mathrm{{\rm K}}}_{\mathrm{j}1}}\left({\mathrm{{\rm X}}}_{\mathrm{i}}\right),{\phi }_{{\mathrm{{\rm K}}}_{\mathrm{j}2}}\left({\mathrm{{\rm X}}}_{\mathrm{i}}\right),\dots ,{\phi }_{{\mathrm{{\rm K}}}_{\mathrm{j}\mathrm{T}}}\left({\mathrm{{\rm X}}}_{\mathrm{i}}\right)\right\}=\left\{{\phi }_{{\mathrm{{\rm K}}}_{\mathrm{j}\mathrm{T}}}\left({\mathrm{{\rm X}}}_{\mathrm{i}}\right),\mathrm{t}=\mathrm{1},\mathrm{T}\right\}$ of alternative $x_i$ to private criteria ${\mathrm{{\rm K}}}_{\mathrm{j}1},{\mathrm{{\rm K}}}_{\mathrm{j}2},\dots ,{\mathrm{{\rm K}}}_{\mathrm{j}\mathrm{T}}$ where ${\mathrm{W}}_{\mathrm{j}1}$, ${\mathrm{W}}_{\mathrm{j}2}$ , … , ${\mathrm{W}}_{\mathrm{j}\mathrm{T}}$ are coefficients of private criterion relativities. A resultant of private criteria is a membership function of alternative $x_i$ to generalized criterion ${\mathrm{{\rm K}}}_{\mathrm{j}}$ ${\phi }_{{\mathrm{{\rm K}}}_{\mathrm{j}1}}\left({\mathrm{{\rm X}}}_{\mathrm{i}}\right)=\underset{t=1}{\overset{\mathrm{T}}{\sum }}{W}_{jt}{\phi }_{k_{jt}}\left(x_i\right)$ .

2. Determination of the membership function of alternative $x_{\mathrm{j}}$ to generalized criterion К ${\phi }_k\left(x_{\mathrm{i}}\right)=\underset{j=1}{\overset{m}{\sum }}{W}_j{\phi }_{k_j}\left(x_i\right)$ where $W_j$, $j=\stackrel{-}{1,m}$ is a coefficient of relativities of criterion $K_j$, $j=\stackrel{-}{1,m}$ .

3. Selection of an alternative with the maximum degree of membership to generalized criterion К $\phi \left(x\right)=max\left\{{\phi }_k\left(x_i\right),i=\stackrel{-}{1,n}\right\}$ where n is a number of alternatives.

Findings

Determination of coefficients of criterion relativities, membership functions of alternatives to criteria is a crucial task. To this end, different approaches are applied (for example, a pairwise comparison method or a method for determining coefficients of criterion relativities based on the expert point rating system).

1. The pairwise criteria comparison method based on quality estimates uses linguistic variables of the Saati table.

2. Coefficients of criteria relativities are determined based on the expert point rating system. Let us assume that L experts assess criteria. To determine criteria relativities $k=\left\{k_i,j=\stackrel{-}{1,m}\right\}$ , a total point is calculated for each criterion $\underset{j=1}{\overset{L}{\sum }}{K}_{j1}$. The sum of points is calculated by all the criteria $\underset{j=1}{\overset{m}{\sum }}\underset{1=1}{\overset{L}{\sum }}{K}_{j1}$ where К _jl isa point of criterion К _j according to the opinion of expert l.

To assess the satisfaction degree for the membership function of alternative $x_{\mathrm{i}}$ to private criteria $K_{j1},K_{j2},\dots ,K_{jT}$, quality gradations (high, middle, low) are assigned to each element of a subset of criteria , and their fuzzy correspondences are determined. Values of individual fuzzy estimates from a corresponding definition area of the interval are determined [0,1]. Then individual expert estimates are integrated in a collective fuzzy estimate of gradations.

Conclusion

The individual estimate that is considered as generalized is generated by an expert who selects the membership measure which is most distant from extreme estimates suggested by experts.

On the basis of the results obtained (membership functions of alternatives to criteria ${\phi }_{k_1}\left(x_1\right)$ , $j=\stackrel{-}{1,m}$ and coefficients of criteria relativities $w_j$ , $j=\stackrel{-}{1,m}$ ), the membership function of alternative $x_i$ to generalized criterion К of the upper level can be determined. Systematization of the results obtained allows ranking the elements from best to worst taking into account conditions ${\phi }_{k_1}\left(x_2\right)>{\phi }_k\left(x_n\right)>\dots >{\phi }_k\left(x_1\right)$ .

The element corresponding to the alternative and meeting condition ${\phi }_{k_1}\left(x\right)=max\left\{{\phi }_k\left(x_i\right),i=\stackrel{-}{1,n}\right\}$ is a leader in the systematized list of individual conclusions.

The methods for developing behavioral business strategies using the fuzzy set theory can be used to develop models of efficient resource management and assess preoccupation of workers with labor performance. An integral index gives an idea of the use of resources in terms of their availability and allows controlling their efficient development. If resources are limited, additional ones can be used.

Using estimates in the form of statements “the business potential is unsatisfactory” (which corresponds to the scale interval from 0 to 4) or “normal” (the scale interval from 4 to 7), or “good” (the scale interval from 8 to 10), any strategy can be assessed. Based on the information received using the fuzzy set theory, business behavior control can be efficient

Acknowledgments

The authors acknowledge that their research was not supported as a part of the government research program of Irkutsk National Research Technical University. The authors bear responsibility for all the errors and heavy style of the manuscript

References

1. Cayir Ervural, B., Zaim, S., Demirel, O. F., Aydin, Z., Delen, D. (2018). An ANP and fuzzy TOPSIS-based SWOT analysis for Turkey’s energy planning Renewable and Sustainable Energy Reviews. 82, 1538-1550. doi: https://doi.org/10.1016/j.rser.2017.06.095
2. Kofman, A. (1982). Introduction to the fuzzy set theory. Moscow: Radio i svyaz, 85 432.
3. Cengiz Toklu, M., Erdem, M.B., Taşkın, H. (2016). A fuzzy sequential model for realization of strategic planning in manufacturing firms Computers & Industrial Engineering. 102, 512-519. doi: https://doi.org/10.1016/j.cie.2016.01.002 
4. Orlivsky, S.A. (1981). Problems of decision making at fuzzy initial information. Moscow: Nauka, 85. 208.
5. Saati, T. (1993). Decision making. A hierarchy analysis method. Moscow: Radio i svyaz, 12. 315.
6. Samarukha, V.I., Skorobogatova, Y.A. (2009). Human capital development financing in municipal education systems. Irkutsk: BSUEL, 45, 441.
7. Zadeh, L.A. (1973) Outline of a new approach to the analysis of complex systems and decision processes. IEEE transactions syst., man, cybern. 3, 28-44.
8. Zakharov, S.V., Bovkun, A.S., & Vasiliev, K.O.  (2017). The functioning of small innovative enterprises created in partnership with state universities and natural persons. Quality Management, Transport and Information Security, Information Technologies, 32-33.
9. Zhukovin, V.E. (1986). Fuzzy multicriteria tasks of decision making. Journal of the AS of the USSR. Cybernetics, 2, 129-133.