Tourism Development Prediction Model For Irkutsk Oblast

Abstract

At the present time, tourism plays a crucial role in the world economy. Revenues derived from the tourism sector can be one third of all budget revenues. It is true for both national and regional economies. The study seeks to develop a mathematical tourist flow model for Irkutsk oblast. The model is designed to predict an increase in the number of tourists taking into account seasonal fluctuations for the next two years. The study is based on the theory of data collection and processing, methods of time series analysis, and Fourier analysis. Based on the statistics, the author developed regression equations connecting tourist flows and revenues of the consolidated budget of Irkutsk oblast which can be used to predict conditions of tourism industry development for the next two years. Besides, a mathematical model for seasonal fluctuations was developed. The model can be used to calculate the number of tourists for Irkutsk oblast.

Keywords: Tourist flowpredictionconsolidated budgetseasonal fluctuations

Introduction

Currently, tourism plays a crucial role in the world economy. The tourism sector is rapidly growing. For example, in 1950, the number of tourists around the world was 25 million people, and the tourism industry turnover was 2.1 billion dollars. In 1987, according to the World Tourism Organization, these numbers were 363 million people and 150 billion dollars respectively. According to the data of 2002, the number of tourists around the world was more than 500 million people and the tourism industry turnover was about 250 billion dollars.

Most international tourists visit economically developed countries. For example, the revenues of Spain and Austria derived from the tourism sector are about one third of all budget revenues. Spain, Austria, France, Italy and Switzerland have positive balances in the tourism sector. At the same time, some Western countries with developed tourism facilities have negative balances in the tourism sector (e.g., Germany and Japan) (UNWTO World Tourism Organization, 2015).

There are three goals of international tourism: recreation, research and business. The share of recreation tourism is more than 70% of all tourist arrivals; the share of research and business tourists is about 15%.

Russia, being the largest country in the world, has significant tourism resources. According to some experts, it can receive about 40 million foreign tourists every year (Rebysheva, & Vasilchenko, 2014). However, in 2014, the number of tourists in Russia was about 2.6 million people. About 6.3 million people were business tourists. The annual number of foreign tourists was 8.9 (Federal Tourism Agency, 2016).

From a recreation perspective, one of the most attractive tourist places in Russia is Lake Baikal listed as a UNESCO world heritage site. Besides, in Irkutsk oblast there are 78 natural landmarks (including 4 federal, 30 regional and 44 local ones), 13 regional natural reserves, 1500 remarkable sights, the Baikal-Lensk and Vitim natural reserves, and the Pribaikal National Park (Fedotov, 2015; Barasheva & Zedgenizova, 2016). Irkutsk oblast has tourism and recreation resources which should be developed to eliminate seasonal fluctuations.

Problem Statement

Seasonal fluctuations are serious obstacles for providing tourist service. In hot seasons, transport, accommodation, and catering challenges are not rare. Low demand for hotel rooms during the year is one of the negative consequences of seasonal fluctuations. In order to attract tourists to the popular regional destinations or to develop new services, tourism companies implement flexible price policies or develop new tourist products, e.g. winter travels (Travel to the Paradize, 2016; Barasheva & Zedgenizova, 2014). Therefore, short-term prediction model development for tourist flows can increase profitability of tourist companies (Vinogradova, 2010; Panina, 2009).

Research Questions

The tourist flow prediction model describes statistical data and seasonal fluctuations. Annual assessment of tourist flows is based on statistical data for previous periods. Seasonal fluctuations of the number of tourists are different for each region and can be determined based on long-term observations of tourist flows by months.

Purpose of the Study

The article aims to develop a mathematical tourist flow prediction model for Irkutsk oblast. The model is designed to predict an increase in the number of tourists taking into account seasonal fluctuations for the next two years.

Research Methods

The study is based on the theory of data collection and processing, time series analysis, and Fourier analysis.

The current level of regional tourism development can be described using data on the number of tourists in Irkutsk oblast for the previous seven years (Figure 1 ):

See Full Size >

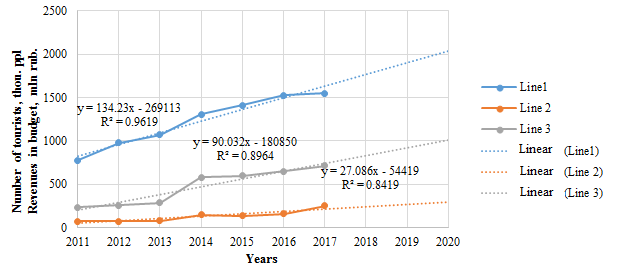
As can be seen, the indices of inbound and outbound tourism improved. In 2017, the number of tourists in Irkutsk oblast increased compared to the previous year. 1547.2 tourists visited Irkutsk oblast. The number of foreign tourists was 250 000. The number increased due to changing ruble exchange rates and international policies aimed at decreasing inbound barriers.

Most foreign tourists in Irkutsk oblast are from China. The trend was typical of 2017 as well. A lot of tourists arrive from the Republic of Korea, Germany, France, Mongolia, the USA, Great Britain, Poland, and Switzerland [Agency for Tourism of the Irkutsk Region. Foreign tourists and tourists from other Russian regions visit Irkutsk oblast with cultural, medical, ecological, business or private purposes.

Statistical data are used to determine trends and predict tourist flows for the next two years. For example, the total number of tourists will increase up to 2031.6 thousand people, 121 thousand of them will be foreign tourists. The regional budget revenues will be 950 million rubles.

One of the peculiarities of the regional tourism is its seasonal fluctuations. It is one of the factors which increase costs of tourist products (Market. Finance. The property, 2016). Seasonal fluctuations in the tourism industry intensify contradictions between the elastic demand for tourist services and the stable tourist supply. Tourist products cause seasonal fluctuations of prices in summer seasons which increases a seasonal demand for tourist products. The seasonal nature of tourist demand causes irregularities in activities of tourist companies following the dynamics of tourist arrivals. Seasonal fluctuations in the tourism industry influence the profitability of other industries which render tourist services (Narziev, 2017).

Figure 2 shows a diagram of changes in the tourist flow in Irkutsk oblast (Vinokurov, 2008):

See Full Size >

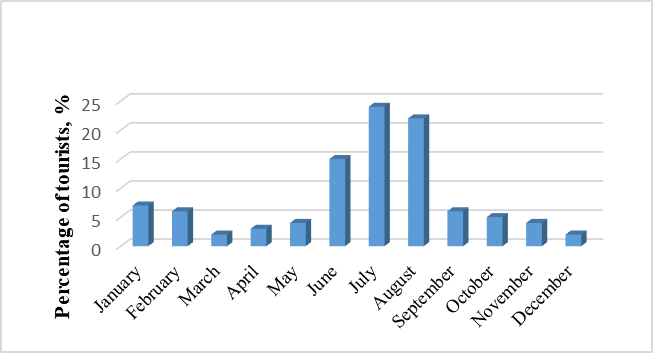
To analyze the behavior of time series with regular fluctuations and develop a mathematical model, the method of Fourier analysis was used (Yurov, 2015; Protasov & Yurov, 2015). The behavior is divided into sine and cosine functions of different frequencies:

$${\mathit{y}}_{\mathit{n}}=\frac{{\mathit{a}}_{\mathit{0}}}{\mathit{2}}+\underset{\mathit{n}=\mathit{1}}{\overset{\mathit{N}}{\sum }}{\mathit{a}}_{\mathit{n}}\mathbf{cos}(\mathit{n}\frac{\mathit{2}\mathit{\pi }}{\mathit{T}}\mathit{t})+\underset{\mathit{n}=\mathit{1}}{\overset{\mathit{N}}{\sum }}{\mathit{b}}_{\mathit{n}}\mathbf{sin}(\mathit{n}\frac{\mathit{2}\mathit{\pi }}{\mathit{T}}\mathit{t}\mathbf{)}$$

where а₀, а_n and b_n are Fourier ratios; n is the number of harmonics; N is the number of observations, Т is a period.

Fourier ratios are calculated by formula:

$${\mathit{a}}_{\mathit{0}}\approx \frac{\mathit{2}}{\mathit{N}}\underset{\mathit{n}=\mathit{1}}{\overset{\mathit{N}}{\sum }}{\mathit{y}}_{\mathit{n}};\mathit{}\mathit{}{\mathit{a}}_{\mathit{n}}\approx \frac{\mathit{2}}{\mathit{N}}\underset{\mathit{n}=\mathit{1}}{\overset{\mathit{N}}{\sum }}{\mathit{y}}_{\mathit{n}}\mathbf{cos}(\mathit{n}\frac{\mathit{2}\mathit{\pi }}{\mathit{T}}\mathit{t});\mathit{}\mathit{}{\mathit{b}}_{\mathit{n}}\approx \frac{\mathit{2}}{\mathit{N}}\underset{\mathit{n}=\mathit{1}}{\overset{\mathit{N}}{\sum }}{\mathit{y}}_{\mathit{n}}\mathbf{sin}\left(\mathit{n}\frac{\mathit{2}\mathit{\pi }}{\mathit{T}}\mathit{t}\right)$$

The amplitude spectrum (Figure 3 ) shows that all five harmonics are significant. They describe seasonal fluctuations of tourist flows.

See Full Size >

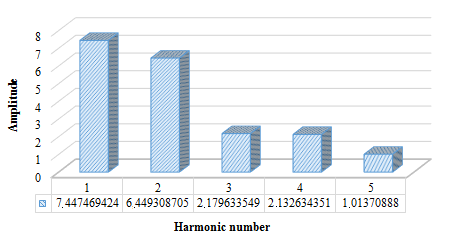
The mathematical model describing seasonal fluctuations by months is as follows:

$$y=\frac{16.6}{2}-7.37\cos \left(1\frac{2\pi }{12}t\right)-1.15\sin \left(1\frac{2\pi }{12}t\right)+6.25\cos \left(2\frac{2\pi }{12}t\right)+1.57\sin \left(2\frac{2\pi }{12}t\right)-2.17\cos \left(3\frac{2\pi }{12}t\right)-\mathit{0.15}\mathbf{sin}\left(\mathit{3}\frac{\mathit{2}\mathit{\pi }}{\mathit{12}}\mathit{t}\right)+\mathit{1.42}\mathit{c}\mathit{o}\mathit{s}\left(\mathit{4}\frac{\mathit{2}\mathit{\pi }}{\mathit{12}}\mathit{t}\right)+\mathit{1.58}\mathit{s}\mathit{i}\mathit{n}\left(\mathit{4}\frac{\mathit{2}\mathit{\pi }}{\mathit{12}}\mathit{t}\right)+\mathit{1.01}\mathit{c}\mathit{o}\mathit{s}\left(\mathit{5}\frac{\mathit{2}\mathit{\pi }}{\mathit{12}}\mathit{t}\right)+\mathit{0.01}\mathit{s}\mathit{i}\mathit{n}\left(\mathit{5}\frac{\mathit{2}\mathit{\pi }}{\mathit{12}}\mathit{t}\right)$$

where у is the relative number of tourists, %; t is the month number.

Findings

The short-term tourism flow prediction model can influence the profitability of tourist companies. The model describes both trend components and seasonal fluctuations of tourist flows.

Conclusion

To conclude, let us provide an example. The task is to calculate the number of tourists, including foreign tourists, and regional budget revenues for 2019.

The solution. The total number of tourists, including the foreign ones, and regional consolidated budget revenues for 2019 can be calculated using regression equations and the data in Figure 1 .

The total number of tourists is:

У1=134.23х+269113=134.23*1019-269113=1897.37 thousand.

The number of foreign tourists is:

У2=27.086х-54419=27.086*2019-54419=267.63 thousand.

The consolidated budget revenues are:

У3=90.032х-180850=90.032*2019-180850=924.608 million rubles.

The additional task is to calculate the total number of tourists in July 2019.

Using the mathematical model (3) or data in Figure 2 , let us determine the relative number of tourists in July 2019:

${у}_{July}=\frac{16.6}{2}-7.37\cos \left(1\frac{2\pi }{12}7\right)-1.15\sin \left(1\frac{2\pi }{12}7\right)+6.25\cos \left(2\frac{2\pi }{12}7\right)+1.57\sin \left(2\frac{2\pi }{12}7\right)-2.17\cos \left(3\frac{2\pi }{12}7\right)$-

$$-\mathit{0.15}\mathbf{sin}\left(\mathit{3}\frac{\mathit{2}\mathit{\pi }}{\mathit{12}}\mathit{7}\right)+\mathit{1.42}\mathit{c}\mathit{o}\mathit{s}\left(\mathit{4}\frac{\mathit{2}\mathit{\pi }}{\mathit{12}}\mathit{7}\right)+\mathit{1.58}\mathit{s}\mathit{i}\mathit{n}\left(\mathit{4}\frac{\mathit{2}\mathit{\pi }}{\mathit{12}}\mathit{7}\right)+\mathit{1.01}\mathit{c}\mathit{o}\mathit{s}\left(\mathit{5}\frac{\mathit{2}\mathit{\pi }}{\mathit{12}}\mathit{7}\right)+\mathit{0.01}\mathit{s}\mathit{i}\mathit{n}\left(\mathit{5}\frac{\mathit{2}\mathit{\pi }}{\mathit{12}}\mathit{7}\right)=\mathit{24}\mathit{\%}$$

Multiplying the total number of tourists in 2019 by the relative number of tourists in July, the number of tourists in July 2019 can be calculated by formula:

УJuly=У1*уJuly /100=1897.37*24/100=455.36 thousand.

References

1. Agency for Tourism of the Irkutsk Region. (n.d.). Reports on the activities of the tourism agency of the Irkutsk region. Retrieved from http://irkobl.ru/sites/tour/report/
2. Barasheva, E.V., & Zedgenizova I.I. (2014). Development and planning issues for small and medium-size businesses in the tourism industry in Baikalsk and the Baikal region. Monograph. Irkutsk: ISTU.
3. Barasheva, E.V., & Zedgenizova, I.I. (2016). Tourism development perspectives in the Baikal region. Management of economic systems. Scientific electronic journal, 7, 89, 11. Retrieved from http://vecs.ru/regionalnaya-ekonomika/item/4008-2016-06-28-08-08-44.
4. Federal Tourism Agency, (2016). Ministry of Culture of the RF. Retrieved from http://www.russiatourism.ru.
5. Fedotov, D.Y. (2013). Problems of tourism development in Irkutsk oblast. Modernization of the economy of the region, 3(77), 48-53.
6. Market. Finance. The property. (2016). Tourseason in Irkutsk was a success: the flow of tourists for 9 months of 2016 increased by 33%. Retrieved from http://sia.ru/?section=484&action=show_news&id=336029
7. Narziev, M.M., (2017). Seasonality of demand for travel services and ways minimization of the seasonal character in the tourism industry Uzbekistan. Retrieved from http://nbisu.moy.su/_ld/5/521_Narziev_ISU.pdf
8. Panina, Z.I., & Vinogradova, M.V. (2009). Management and planning of the enterprise in the service industry. Moscow: Dashkov and K.
9. Protasov, Y.M., & Yurov, V.M. (2015). Simulation of seasonal and cyclic fluctuations of sales volumes using Fourier analysis in MS Еxcel. Bulletin of Moscow State Oblast University. Series: Economics, 2, 101-108.
10. Rebysheva, L.V., & Vasilchenko, E.V. (2014). Inbound business tourism: development in Russia. University science: theoretical and methodological problems of training specialists in economics, management and law, 11, 160-163.
11. Travel to the Paradize, (2016). Recreational district formation. Tourist centers - seasonal problems in international tourism. Retrieved from http://you2way.ru/rekreacionnaya-geografia/79-rekreatsionnoe-rajonoobrazovanie-turisticheskie-tsentry?start=16Vinokurov, М. А. (2008).  The economy of Irkutsk oblast. Vol. 4. Irkutsk: BGUEP.
12. UNWTO World Tourism Organization, (2015). Why tourism? Retrieved from http://www2.unwto.org/content/why-tourism
13. Vinogradova, M.V., Panina, Z.I., Larionova, А.А., etc. (2010). Business planning in the hospitality industry: a textbook. Moscow: Dashkov and K.
14. Yurov, V.M. (2015). Simulation of non-stationary time series with pronounced fluctuations using Excel tools. Bulletin of Moscow State Oblast University. Series: Economics, 1, P. 62-71.