Numerical Estimation Abilities In Russian School-Age Children: Evidence Of Exponential Growth

Tayler Truhan ,
Georgy Vasin ,
Tatiana Tikhomirova ,
Sergey Malykh

Abstract

Numerical estimation abilities develop as children age and gain increased number knowledge. Estimation abilities stem from the approximate number system, a cognitive system present from infancy. Using a cross-sectional design, the aim was to study age differences in numerical estimation abilities and to examine the nature of this relationship. The number line task with a “0” on the left end of the line and with “1,000” on the right was utilised with a unique sample of Russian school children. We collected data from students at each grade level, from elementary to high school. The sample consisted of 1,056 students from 7 to 18 years old (M = 11.82, SD = 3.17), 49% female. Children showed significant improvements in estimation abilities in young childhood, followed by stabilisation in adolescence. Significant levels of improvement in number line placement were shown up to Grade 5, reaching a plateau after Grade 6. These results support previous research that has highlighted periods of improvement in estimation abilities in primary school. This exponential model of improvement parallels the development of cognitive abilities, which show sharp peaks in childhood, followed by stabilisation in adolescence. Future research will aim to conduct an in-depth exploration of the logarithmic to linear shift that hallmarks improvement in numerical estimation abilities.

Keywords: Number linenumerical estimationschool yearscross-sectional

Introduction

Estimation is utilised by children and adults to solve a wide-variety of problems, both in education and everyday life. Estimation involves the ability to understand and relate numbers, or number sense. This ability stems from the approximate number system (ANS), which is a cognitive system present in both nonhuman animals and humans from infancy that is linked to basic numerical intuitions (Halberda, Ly, Wilmer, Naiman, & Germine, 2012). Estimation abilities may be measured through tests of numerical estimation on a number line (NL). The NL has been highlighted as a basic mathematical tool that is central to many areas of mathematics, such as geometry and algebra (Geary, Hoard, Nugent, & Byrd-Craven, 2008; National Council of Teachers of Mathematics, 2006). NL tasks may provide insight into the development of children’s understanding of numerical magnitudes, which is integral to estimation. Success in numerical estimation has been linked with present and future school achievement and math processing abilities, such as arithmetic, numerical categorisation, and numerical magnitude comparison (Booth &Siegler, 2008; Friso-van den Bos et al., 2015; Siegler, Thompson, & Opfer, 2009; Tikhomirova et al., 2015). When assessing primary school children, proficiency at numerical estimation has been shown to improve with age and grade level (Booth & Siegler, 2006; Siegler & Booth, 2004). Education has an effect on estimation abilities above and beyond that of age, in that it is necessary to learn words for numbers and other important concepts, such as arithmetic operations (e.g., Tikhomirova, Kuzmina, & Malykh, 2018; Tikhomirova et al., 2017). This is evidenced in research conducted with Amazonian tribes that do not have words for large numbers and receive no formal education, and consequently show poor abilities in numerical estimation and exact arithmetic (Pica, Lemer, Izard, & Dehaene, 2004).

Individual differences in children’s linearity of estimates on NL tasks have been associated with scores on mathematics tests in primary school (Booth & Siegler, 2006). As children age and gain familiarity with a wider variety of numbers, their mental representation of a NL shifts from logarithmic to linear, with numbers placed more accurately on a 0-100 NL (Booth & Siegler, 2008; Geary et al., 2008). Children with mathematical learning disabilities have shown difficulty with numerical estimation, in so far that it takes longer to develop a linear mental NL (Geary et al., 2008). This suggests that age, cognitive abilities, and mathematics education contribute to children’s numerical estimation abilities. Research on the development of mental representation of numbers and numerical estimation is applicable to cognitive psychology and theory and to education and schooling curriculum.

Development of numerical estimation skills

Extant research on children’s numerical estimation skills has highlighted the developmental shift from a logarithmic to a linear representation of numbers, whereby accuracy on NL tasks increases with age (Booth & Siegler, 2006; Slusser & Barth, 2017; Slusser, Santiago, & Barth, 2013; Thompson &Opfer, 2008). This transition occurs at different time points based on the number scale utilised in the NL task. Increased accuracy on the NL task occurs between kindergarten and second grade for a 0-100 scale, between second and fourth grade for a 0-1,000 scale, and between third and sixth grade for a 0-100,000 scale (Opfer & Siegler, 2007; Siegler et al., 2009). Younger children more often place large numbers closer together on a NL task, suggesting they may have difficulty processing larger numbers due to unfamiliarity (Ebersbach, Luwel, Frick, Onghena, & Verschaffel, 2008). They are also less likely to use the highlighted midpoint as a reference, and may rely only on the two endpoints (Slusser & Barth, 2017). This pattern of growth in estimation accuracy that occurs in primary school is further highlighted by the pattern of childhood peaks and adolescent plateaus that occurs in cognitive development (Giedd, 2008).

Number line acuity

At a young age, children show a dramatic improvement in NL estimation skills. Second and third grade children show half of the absolute error in estimation accuracy when compared to children in kindergarten (Booth & Siegler, 2006). As familiarity with a greater number span increases, so does the linearity of NL estimations. Extant research has shown that children in second grade use a linear strategy on a 0-100 NL task, but yet still use a logarithmic strategy when faced with a 0-1000 NL (Siegler & Booth, 2004). Younger children may exhibit poor working memory competence in comparison to adolescents due to incomplete development of executive processing abilities (De Luca et al., 2003). The number line task is linked to spatial working memory, in that children with poor arithmetic skills also exhibit impaired spatial working memory (McLean & Hitch, 1999). This suggests that there are specific developmental time-points during which children may show greater NL acuity as their cognitive skills continue to improve.

Problem Statement

In order to further elucidate the development of numerical estimation abilities, the current study assessed the relationship between grade level and NL scores. This assessment aimed to show the developmental trajectory of numerical estimation abilities throughout childhood and adolescence. Much of the extant research explores numerical estimation skills solely in primary school children (Booth & Siegler, 2006; Ebersbach et al., 2008; Friso-van den Bos et al., 2015), so to gain a more comprehensive picture this study included children aged 7-18.

Research Questions

Performance on the NL task varies with age and education level. This pattern of improvement does not follow a linear model, which is evidenced by the shift in performance that occurs at different grade time points (Opfer & Siegler, 2007; Siegler et al., 2009). There is a lack of extant research that measures numerical estimation abilities over the course of school-age development. The current study aims to address this gap by exploring performance on the NL task in a unique sample of Russian children aged 7 – 18. Cognitive abilities, such as numerical estimation, have been shown to continue developing into young adulthood (Giedd, 2008), which is why it is important to study these patterns in a wider age range.

Purpose of the Study

Assessing numerical estimation abilities over the course of school-age development will aid in understanding the cognitive mechanisms that underlie estimation skills. Our objective in this study was to model the growth of estimation abilities over time, which we approached by observing a sample of children aged 7-18 in a cross-sectional design. Although the current study was not longitudinal, the large range in age allowed for measurement of the development of numerical estimation abilities. The sample for the current study is unique in that it included over 1,000 participants, and was drawn from families of different socioeconomic backgrounds in various Russian cities. This will allow us to gain a more comprehensive picture of the effects of grade level on the development of numerical estimation abilities throughout childhood and adolescence, which is vital to our understanding of cognitive characteristics and to education curriculum planning.

Research Methods

Sample

We collected data from students at each grade level, from elementary to high school. Our sample consisted of 1,056 students from7 to 18 years old (M = 11.82, SD = 3.17), 49% female. Table 1 demonstrates the standard deviations of age (in months) between students in each grade. Note that our sample was cross-sectional.

Data collection

We studied participants’ numerical estimation with a computerized version of the NL test, which was adapted from a description given in (Siegler & Opfer, 2003). In this version of the NL, participants are presented with a line on the screen, the left end of the line is marked with a “0” and the right end – with “1,000” (Tosto et al., 2013). Participants are asked to place a mark on the line, corresponding to the number on top of the screen. There are 22 tasks in this test, and the order they are presented in is the same for all participants. The test also starts with one training task to familiarize participants with the test interface. Each task is scored as the absolute deviation of the estimate from the target number, and the total score is the mean of all task scores.

Analysis

We used multiple linear regression to compare the performance of age and grade as predictors for NL scores. Afterwards, in order to measure the growth of estimation abilities over time, we fit various regression models to the data: linear, polynomial and exponential. We chose the best model by the amount of NL score variance explained, given acceptable model fit. Parameter estimation was performed in R (Team, 2014) with the least squares estimator.

Findings

As expected, the NL score (which is a measure of estimation error, not proficiency) got lower with age, with the most noticeable reduction occurring between the 1st and 5th grades. After grade 6 we can see that the reduction becomes much slower, which hints at the relationship between NL scores and grade level being exponential – with a fast initial decline, that slows down after a certain point.

Table 1 -
See Full Size >

Since we are looking at the development of estimation abilities with age, our choice of predictor variables was between age (in months) and grade. Even though the two are highly correlated in our sample (r=0.987), they do not represent the same thing. For example, Pica and colleagues (2004) demonstrated that education can have a unique effect on the development of estimation skills, beyond that of age. Given the considerable variance of the age of students inside each grade in our sample, we wanted to see how age and grade would interact as predictors of NL scores. For this purpose, we fit a multiple linear regression to the data. The two predictors together explained 32% of the variance in NL scores (R2=0.323, F(3, 949)=152.8, p < 0.0001). When put together into one model, age was still technically a significant predictor (β = -0.35, p < .05). However, it barely added anything to the model in comparison to grade (β = -1.64, p < .0001). This finding points towards education being a more important factor than age in the development of estimation skills, and falls in line with Pica and colleagues’ results. However, the fact that age is not a completely irrelevant predictor prompts additional research to further elucidate the unique effects that age and education bring to the development of estimation skills.

Following the results of our multiple regression analysis, we decided to proceed with grade as the single predictor for NL scores. Next, we fit various regression models to study their relationship further.

Table 2 -
See Full Size >

All models had acceptable fit to the data. The results of the linear model show that NL scores decline in higher grades. The linear model explained 28% of the variance in NL scores, which was the lowest R squared out of all the models. Next, we fit two polynomial models to check for non-linearity in the relationship between NL scores and grade. Indeed, both the quadratic and cubic regression models explained more variance of the dependent variable than the linear model (R2 = 0.32 and R2 = 0.33 respectively), which indicated that the relationship is non-linear. Finally, we fit an exponential regression model. Under the exponential model, grade explained the most variance in NL scores: 38%. Figure 1 demonstrates that an exponential curve fits the distribution of NL scores quite well. The exponential model explained the most variance and had the least number of parameters, so we can conclude that out of the 4 examined regression models, it has the best fit to our data.

To sum up, performance on the NL improves exponentially with grade. Judging by the distribution of NL scores, this trend slows down after grade 5. Indeed, if we fit a linear regression on grade to the NL scores of all children in grade 5 and beyond, it explains only 3% of the variance, indicating that grade almost doesn’t impact scores in that age range.

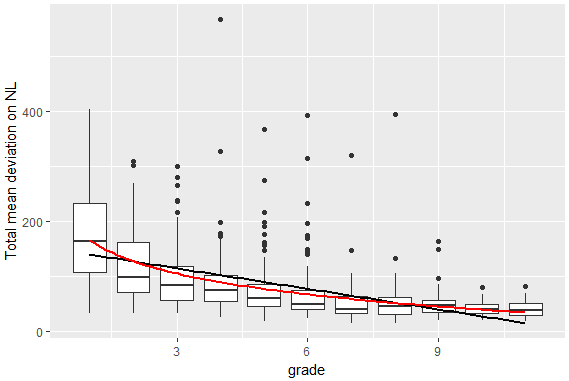
Figure 1: NL scores by grade. NL scores in each grade are represented by boxplots, with a linear regression line (in black) and an exponential regression curve (in red).
NL scores by grade. NL scores in each grade are represented by boxplots, with a linear regression line (in black) and an exponential regression curve (in red).
See Full Size >

The results obtained in the current study support the trend in the development of cognitive characteristics, which follows sharp increases in young childhood to declines or plateaus in adolescence. There was great improvement shown from Grade 1 to Grade 5, yet almost no significant improvement observed in the grades thereafter. Extant research has highlighted the increase in NL acuity that occurs at Grade 2, Grade 4, and Grade 6 for various NL lengths (Opfer & Siegler, 2007; Siegler et al., 2009). ANS acuity, the cognitive system underlying numerical estimation abilities, has been significantly linked with mathematics abilities in childhood (Halberda, Mazzocco, & Feigenson, 2008), and yet shows no significant association in adults (Inglis, Attridge, Batchelor, & Gilmore, 2011). In childhood, both the ANS and numerical estimation abilities are developing at a rapid pace, which can be seen in the current study via significant improvement in estimation skills up to Grade 5. However, the association between ANS acuity and mathematics achievement decreases with age (Inglis et al., 2011), which supports the results of the current study in which NL abilities show moderate improvements in later adolescence. This suggests that in terms of numerical estimation, age may be considered less significant in comparison to other influential factors, such as receiving formal education and the acuity of inherent cognitive abilities.

Conclusion

In this study we examined the overall accuracy of numerical estimation in Russian school children from all 11 grades, which revealed results comparable to those from other populations. Furthermore, the results of the current study are robust in both size and sampling of the population. The sample utilised in the current study stemmed from different socioeconomic backgrounds and cities in Russia. In comparison to other studies assessing numerical estimation via the NL task, the current sample spanned a wider age range, which allowed for a more comprehensive assessment of the development of numerical estimation abilities.

Children shift from a logarithmic to linear mental representation of numbers at several time-points in response to an increasing NL (Opfer & Siegler, 2007; Siegler et al., 2009). In future research, we plan to examine the task-level performance on the NL across different age groups in order to find evidence of the types of numerical representation children use at various ages. Contemporary research has highlighted the parallel increase in number knowledge and linear responding to the NL task that occurs in young children (Ashcraft & Moore, 2012). Assessing which model of NL placement children use within a large sample and with a wider age range will add to the existing literature by giving the results greater power and generalisability.

Acknowledgments

This study was supported by the grant from the Russian Science Foundation №17-78-30028.

References

  1. Ashcraft, M. H., & Moore, A. M. (2012). Cognitive processes of numerical estimation in children. Journal of experimental child psychology, 111(2), 246-267.
  2. Booth, J.L., & Siegler, R.S. (2006). Developmental and individual differences in pure numerical estimation. Developmental Psychology, 42(1), 189.
  3. Booth, J. L., & Siegler, R. S. (2008). Numerical magnitude representations influence arithmetic learning. Child Development, 79(4), 1016-1031.
  4. De Luca, C.R., Wood, S.J., Anderson, V., Buchanan, J.A., Proffitt, T.M., Mahony, K., & Pantelis, C. (2003). Normative data from the CANTAB. I: Development of executive function over the lifespan. Journal of Clinical and Experimental Neuropsychology, 25(2), 242-254.
  5. Ebersbach, M., Luwel, K., Frick, A., Onghena, P., & Verschaffel, L. (2008). The relationship between the shape of the mental number line and familiarity with numbers in 5-to 9-year old children: Evidence for a segmented linear model. Journal of Experimental Child Psychology, 99(1), 1-17.
  6. Friso-van den Bos, I., Kroesbergen, E.H., Van Luit, J.E., Xenidou-Dervou, I., Jonkman, L.M., Van der Schoot, M., & Van Lieshout, E.C. (2015). Longitudinal development of number line estimation and mathematics performance in primary school children. Journal of Experimental Child Psychology, 134, 12-29.
  7. Geary, D.C., Hoard, M.K., Nugent, L., & Byrd-Craven, J. (2008). Development of number line representations in children with mathematical learning disability. Developmental Neuropsychology, 33(3), 277-299.
  8. Giedd, J.N. (2008). The teen brain: Insights from neuroimaging. Journal of Adolescent Health, 42(4), 335-343.
  9. Halberda, J., Mazzocco, M.M., & Feigenson, L. (2008). Individual differences in non-verbal number acuity correlate with maths achievement. Nature, 455, 665–668.
  10. Halberda, J., Ly, R., Wilmer, J.B., Naiman, D. Q., & Germine, L. (2012). Number sense across the lifespan as revealed by a massive Internet-based sample. Proceedings of the National Academy of Sciences, 109(28), 11116-11120.
  11. Inglis, M., Attridge, N., Batchelor, S., & Gilmore, C. (2011). Non-verbal number acuity correlates with symbolic mathematics achievement: But only in children. Psychonomic Bulletin & Review, 18(6), 1222-1229.
  12. McLean, J.F., & Hitch, G.J. (1999). Working memory impairments in children with specific arithmetic learning difficulties. Journal of Experimental Child Psychology, 74(3), 240-260.
  13. National Council of Teachers of Mathematics (2006). Curriculum focal points for prekindergarten through grade 8 mathematics: A quest for coherence. Reston, VA: Author.
  14. Opfer, J.E., & Siegler, R.S. (2007). Representational change and children’s numerical estimation. Cognitive Psychology, 55(3), 169-195.
  15. Pica, P., Lemer, C., Izard, V., & Dehaene, S. (2004). Exact and approximate arithmetic in an Amazonian indigene group. Science, 306(5695), 499-503.
  16. Siegler, R.S., & Booth, J.L. (2004). Development of numerical estimation in young children. Child Development, 75, 428–444.
  17. Siegler, R.S., & Opfer, J.E. (2006). Representational change and children’s numerical estimation. Cognitive Psychology. doi:10.1016/j.cogpsych.2006.09.002.
  18. Siegler, R.S., & Opfer, J.E. (2003). The development of numerical estimation: evidence for multiple representations of numerical quantity. Psychological Science, 14, 237–243.
  19. Siegler, R.S., Thompson, C.A., & Opfer, J.E. (2009). The logarithmic to linear shift: One learning sequence, many tasks, many time scales. Mind, Brain, and Education, 3(3), 143-150.
  20. Slusser, E., & Barth, H. (2017). Intuitive proportion judgment in number-line estimation: Converging evidence from multiple tasks. Journal of Experimental Child Psychology, 162, 181-198.
  21. Slusser, E.B., Santiago, R.T., & Barth, H.C. (2013). Developmental change in numerical estimation. Journal of Experimental Psychology: General, 142(1), 193.
  22. Team, R C. (2014). R: A language and environment for statistical computing. R Foundation for Statistical  Computing, Vienna, Austria. URL http://www.R-project.org/.
  23. Thompson, C.A., & Opfer, J.E. (2008). Costs and benefits of representational change: Effects of context on age and sex differences in symbolic magnitude estimation. Journal of Experimental Child Psychology, 101(1), 20-51.
  24. Tikhomirova, T., Kuzmina, Yu., & Malykh, S. (2018). Does Symbolic and Non-Symbolic Estimation Ability Predict Mathematical Achievement across Primary School Years? ITM Web of Conferences 2018, 18, 04006
  25. Tikhomirova, T.N., Misozhnikova, E.B., Malykh, A.S., Gaydamashko, I.V., Malykh, S.B. (2017). Mathematical fluency in high school students. Psychology in Russia: State of the Art, 10(1), 95-104.
  26. Tikhomirova, T.N., Voronin, I.A., Misozhnikova, E.B., Malykh, S.B. (2015). The structure of the interrelation of the cognitive characteristics and academic achievement in school age. Teoreticheskaya i ehksperimental'naya psihologiya. 8(8), 55–68.
  27. Tosto, M.G., Tikhomirova, T., Galajinsky, E., Akimova, K., Kovas, Y. (2013). Development and Validation of a Mathematics-number sense Web-based Test Battery. Procedia – Social and Behavioral Sciences, 86, 423-428.

Copyright information

Creative Commons License
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

About this article

Publication Date

23 November 2018

Article Doi

https://doi.org/10.15405/epsbs.2018.11.02.81

eBook ISBN

978-1-80296-048-8

Publisher

Future Academy

Volume

49

Print ISBN (optional)

-

Edition Number

1st Edition

Pages

1-840

Subjects

Educational psychology, child psychology, developmental psychology, cognitive psychology

Cite this article as:

Truhan, T., Vasin, G., Tikhomirova, T., & Malykh, S. (2018). Numerical Estimation Abilities In Russian School-Age Children: Evidence Of Exponential Growth. In S. Malykh, & E. Nikulchev (Eds.), Psychology and Education - ICPE 2018, vol 49. European Proceedings of Social and Behavioural Sciences (pp. 698-705). Future Academy. https://doi.org/10.15405/epsbs.2018.11.02.81

Copy citation text