Algorithms Of The Operator’s Electroencephalogram Analysis Based On The Principal Component Analysis

Principal component analysis

The principal component analysis (Poliev, 2017) is used to reduce the dimension of the observable vectors' space without a significant loss of information content. The principal components are an orthogonal coordinate system where the variances of the components characterize their statistical properties.

Let us take the initial set of vectors X of the linear space $\mathrm{}{\mathrm{L}}^{\mathrm{p}}$. The use of principal component analysis allows us to go to the basis of linear space ${\mathrm{L}}^{{\mathrm{p}}^{\mathrm{\text{'}}}},({\mathrm{p}}^{\mathrm{\text{'}}}\ll \mathrm{p})$ with the following properties: the first component (the first basis vector) corresponds to the direction along which the variance of the vectors of the initial set is maximal; the direction of the second component (the second basis vector) is chosen in such a way that the dispersion of the initial vectors along it is maximal under the condition of orthogonality to the first basis vector. The remaining basis vectors are defined the same way. Thus, the directions of the basis vectors are chosen to maximize the variance of the initial set along the first components, called the principal components. The main variability of the vectors from the initial sets is represented by several first components and it is possible to go to a space of smaller dimension by discarding the less significant components.

Let us take a multidimensional random observation

$X=\left(\begin{array}{c}{x}_{\mathrm{}}^{\left(\mathrm{1}\right)}\\ ⋮\\ x_{\mathrm{}}^{\left(p^{\mathrm{}}\right)}\end{array}\right)$.

The problem is to reduce the number of components from $\mathrm{p}$ to ${\mathrm{p}}^{\mathrm{\text{'}}}$. This task can be solved if we define all possible linear orthogonal normalized combinations ${\mathrm{z}}_{\mathrm{}}^{\left(\mathrm{j}\right)}\left(\mathrm{X}\right)={\mathrm{c}}_{\mathrm{j}\mathrm{1}}({\mathrm{x}}_{\mathrm{}}^{\left(\mathrm{1}\right)}-{\mathrm{\mu }{\mathrm{}}^{\left(\mathrm{1}\right)})}_{\mathrm{}}+\dots +{\mathrm{c}}_{\mathrm{j}\mathrm{p}}({\mathrm{x}}_{\mathrm{}}^{\left({\mathrm{p}}^{\mathrm{}}\right)}-{\mathrm{\mu }{\mathrm{}}^{\left({\mathrm{p}}^{\mathrm{}}\right)})}_{\mathrm{}}$, where $\left[{\mathrm{\mu }{\mathrm{}}^{\left(\mathrm{1}\right)}}_{\mathrm{}},\dots ,\mathrm{\mu }{\mathrm{}}^{\left(\mathrm{p}\right)}\right]{\mathrm{}}^{\mathrm{\text{'}}}$ is the vector of the averages for the variable X. As a measure of the ${\mathrm{p}}^{\mathrm{\text{'}}}$-dimensional system ${(\mathrm{z}}_{\mathrm{}}^{\left(\mathrm{1}\right)}\left(\mathrm{X}\right),\dots ,\mathrm{}{\mathrm{z}}_{\mathrm{}}^{\left({\mathrm{p}}^{\mathrm{\text{'}}}\right)}\left(\mathrm{X}\right))\mathrm{}$informativeness let us take a variable ${\mathrm{I}}_{{\mathrm{p}}^{\mathrm{\text{'}}}}=\mathrm{}\frac{\mathrm{D}{\mathrm{z}}^{\mathrm{1}}+\dots +\mathrm{D}{\mathrm{z}}^{{\mathrm{p}}^{\mathrm{\text{'}}}}}{\mathrm{D}{\mathrm{x}}^{\mathrm{1}}+\dots +\mathrm{D}{\mathrm{x}}^{\mathrm{p}}\mathrm{}}$, where $\mathrm{D}{\mathrm{z}}^{\mathrm{}}$is the operation for calculating the variance of a random variable. It can be shown that the relations for the determination of all $\mathrm{p}$ principal components of the matrix X can be represented in the following form $\mathrm{Z}=\mathrm{L}\mathrm{X}$, where $\mathrm{Z}={(\mathrm{z}}_{\mathrm{}}^{\left(\mathrm{1}\right)},\dots ,\mathrm{}{\mathrm{z}}_{\mathrm{}}^{\left({\mathrm{p}}^{\mathrm{}}\right)})\mathrm{\text{'}},\mathrm{}\mathrm{X}={(\mathrm{x}}_{\mathrm{}}^{\left(\mathrm{1}\right)},\dots ,\mathrm{}{\mathrm{x}}_{\mathrm{}}^{\left({\mathrm{p}}^{\mathrm{}}\right)})\mathrm{\text{'}}$ and the matrix $\mathrm{L}$ contains the rows ${\mathrm{l}}_{\mathrm{j}}=\left({\mathrm{l}}_{\mathrm{j}\mathrm{1}},\dots ,\mathrm{}{\mathrm{l}}_{\mathrm{j}\mathrm{p}}\right),\mathrm{}\mathrm{j}=\mathrm{}\stackrel{-}{\mathrm{1},\mathrm{p}}$, which are eigenvectors of the covariance matrix $\sum \mathrm{}$of the random variable X. Eigenvalues ${\mathrm{}\mathrm{\lambda }}_{\mathrm{j}}$, $\mathrm{}\mathrm{j}=\mathrm{}\stackrel{-}{\mathrm{1},\mathrm{p}}$ correspond to these eigenvectors.

The main properties of the principal components are listed below:

The matrix $L$ is orthogonal, i.e. $L{L}^{\mathrm{\text{'}}}=L^{\mathrm{\text{'}}}L=I$, where $I$ is the identity matrix.

The covariance matrix of the principal components vector:

${\sum }_Z=\mathrm{}L{\sum L}^{\mathrm{\text{'}}}$= $\left(\begin{array}{ccc}{\mathrm{}\lambda }_{\mathrm{1}}& \cdots & \mathrm{0}\\ ⋮& \ddots & ⋮\\ \mathrm{0}& \cdots & {\mathrm{}\lambda }_p\end{array}\right)$.

The sum of the original characteristics’ variances is equal to the sum of all principal components variances.

The criterion of the informativeness: ${\mathrm{I}}_{{\mathrm{p}}^{\mathrm{\text{'}}}}\left(\mathrm{Z}\right(\mathrm{X}\left)\right)=\mathrm{}\frac{{\mathrm{\lambda }}_{\mathrm{1}}+\mathrm{}{\mathrm{\lambda }}_{\mathrm{2}}+\dots +\mathrm{}{\mathrm{\lambda }}_{{\mathrm{p}}^{\mathrm{\text{'}}}}}{{\mathrm{\lambda }}_{\mathrm{1}}+\mathrm{}{\mathrm{\lambda }}_{\mathrm{2}}+\dots +\mathrm{}{\mathrm{\lambda }}_{\mathrm{p}}\mathrm{}}$, where ${\mathrm{\lambda }}_{\mathrm{1}},\mathrm{}{\mathrm{\lambda }}_{\mathrm{2}},\dots ,\mathrm{}{\mathrm{\lambda }}_{\mathrm{p}}$ are the eigenvalues of the covariance matrix Σ of the vector X, arranged in decreasing order. This criterion is the basis for deciding how many of the last principal components can be removed without significant information loss, thereby reducing the dimension of the initial linear space.

Experiment with EEG

In order to study the effect of fatigue on the activities’ characteristics of the operator, the following experiment was carried out. Operator carried out multiple landing approaches at the flight simulator for an hour (19 approaches). As an additional factors increasing the workload were a test, which required a response to a predetermined stimulus (GoNoGo-test), the need to pronounce a predetermined word when the appropriate indicator was turned on. EEG was continuously recorded during the experiment. The duration of the experiment was about an hour.

Experimental results

The EEG analysis was carried out for the spectral densities of the initial signals. For the calculated spectral densities, the following procedure was carried out. We selected seven time intervals duration of 1...2 seconds uniformly distributed over the whole experiment duration of one hour. Also we selected twelve signals, six of them corresponded to brain's alpha rhythms and the remaining six corresponded to theta rhythms. After that for each signal we calculated a percentage of signal information, that was described by first two principal components. Tables 01 – 02 describe the total percentages that are described by the first two principal components for selected signals.

Results analysis shows that first two principal components are the most informative for every signal (they describe about 95-99% of the initial basis). In this regard it is proposed to use only first two principal components as the most informative.

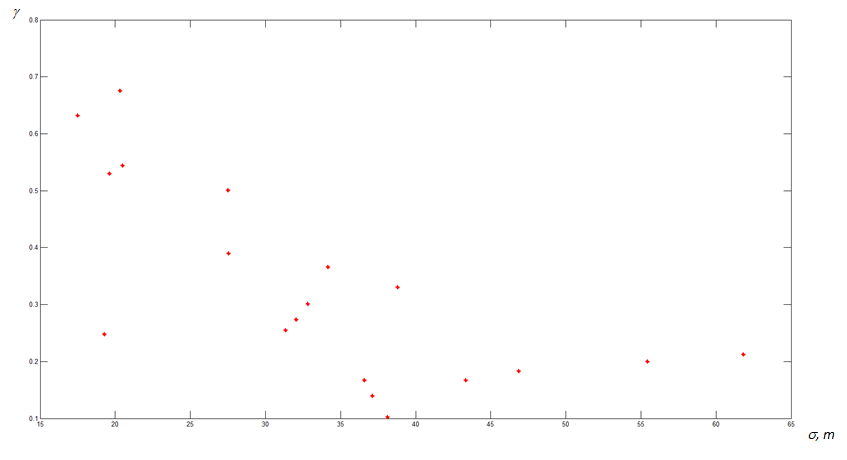
Figure 01 illustrates the plot of the average coherence function between the altitude error (vertical deviation from the glide path) and the operator’s control signal in the longitudinal channel against the altitude error standard deviation. Every single point on the plot corresponds to individual landing approach.

This plot shows that the relationship between the coherence function and the piloting accuracy (altitude error) is approximately exponential. With the exception of a few points, the lower altitude error (or the piloting accuracy) corresponds to the higher values of the average coherence function between the altitude error and the operator's control signal in the longitudinal channel.

See Full Size >

Now let us show that the piloting accuracy is related to the EEG parameters. For these purposes, the principal components were calculated separately for six signals corresponding to the alpha rhythms, and six signals corresponding to the theta rhythms. Thus, two sets of principal components were obtained. As it was shown before, the most informative are the first two principal components. Therefore, the ratios of the norms of the first principal components from both sets were calculated: $\frac{{|PC}_1\left(\alpha \right)|}{{|PC}_1\left(\theta \right)|}$, where ${PC}_1\left(\alpha \right)$ is the first principal component for six alpha signals, ${PC}_1\left(\theta \right)$ is the first principal component for six theta signals. The same way we calculated the ratios of the norms of the second principal components from both sets ( $\frac{{|PC}_2\left(\alpha \right)|}{{|PC}_2\left(\theta \right)|}$). Figure 02 shows the plots of these ratios against the average coherence function between the altitude error and the operator’s control signal in the longitudinal channel.

See Full Size >

This plots show that for both first and second components there is a tendency for the ratio to decrease with an increase in the average coherence function. The decrease in the ratio means that that the values of alpha signals decrease too and operator's attention and mental activity increase. In its turn, when the brain functional activity increases during the piloting, the piloting accuracy also increases.