Fact, Belief, Truth And Cognition In School Mathematics Education

Abstract

The informatization of the society poses new requirements to the education, regarding its quality. 21^st century school should not only give knowledge but also train students to apply it both in learning and real-life scenarios. The authors try to describe the process of the school mathematical education from the point of view of Bertrand Russel’s theory of knowledge – by using the tetrad “fact – belief – truth – knowledge”. This brings a new component into the methodology, connected to the “sources” of the confidence of a student in a learnt mathematical fact. From this point of view, the strictness level of the school mathematics exceeding the students’ experience leads to a belief in the mathematical facts based on the social compliance, i.e. on the positive reaction of the teacher caused by saying or writing of correct words in a correct order. This is shortly formulated as “remember it for now, you will understand later”. In the present article, this is referred to as a “verbal belief”. Such knowledge can be applied in the typical learning context only. A belief based on the student’s experience is, oppositely, a cognitive tool opening a way to researching new mathematical subjects arising in both the science and the everyday life. This belief is referred to as “meaningful”. The article considers the meanings of the words "fact", "faith", "truth" and "cognition", which can be useful for clarifying the philosophical and methodological problems associated with setting up a school mathematics education that meets the requirements of modern school reform.

Keywords: Teaching mathematics methodologymathematical literacy

Introduction

School reforms currently taking place both in our country and abroad are accompanied by a change in the educational paradigm. The appearance of the traditional model of mass education was adapted to the "age of printing", where the school textbook (text of the book itself or, voiced by the teacher) played the role of the foundation of the educational process, and the educational mathematical activity was built around the samples of reasoning and consisted mainly in the formation of appropriate skills. Today, information and telecommunication technologies are playing the leading role in educational practice, and the study of their positive influence and possible risks becomes the object of close attention of the leading scientists and educators (Ivanova, 2016). The era of informatization naturally led to a significant change in the ideas about the results of school mathematics education. In modern Russian educational standards (Federalniya gosudarstvenniye obrazovatelniye standarty obschego obrazovaniya, 2012), as well as in the global system of general education, high-level thinking skills come first. One of the most important indicators of the mathematical preparation of the graduate is mathematical literacy, where it is not so much about the ability to make the calculations necessary in the everyday life of the inhabitant, but also to possess the qualities of thinking necessary for an active citizen. Therefore, the traditional methods of teaching and the visual aids used, which were well adapted to the formation of account skills and simple spatial representations, although not lost their relevance, but no longer provide an exhaustive coverage of the requirements for the level of mathematical preparation of schoolchildren.

The leading educational activity in teaching mathematics is cognitive. In our study, we consider cognition as "the assimilation of the sensory content of the experienced or experienced state of things, states, processes with the aim of finding the truth" (Philosofsko-entsiklopedicheskiy slovar, 2010). The key words for describing the cognitive process in teaching mathematics, following Bertrand Russell (Russel, 1948), we choose: fact, faith, truth and cognition. Thus, in this article we will consider the meanings of the words fact, faith, truth and cognition from the point of view of philosophical and methodological questions concerning school mathematical education.

Problem Statement

We proceed from the assumption that the acquisition of sensory experience, responsible for the accumulation of mathematical facts, is associated with certain difficulties related to the objective feature of mathematics and that mathematical objects, such as the multiplication table or the ratio of the intersection of sets, are not perceived by the senses and not are of a public nature. Partly, therefore, the presentation of many sections of school mathematics traditionally suffers from excessive formalism in the spirit of strict deduction of the "Elements" of Euclid, which, according to historians, was not intended for schoolchildren, but for the exercise of mature men in logically correct theoretical reasoning (Heath, n.d.). With excessive dedication to the deductive nature, the most important methodological aspect, concerning the understanding of mathematical terms and statements, as well as the semantic links of one studied fact with others, escapes. In this case, the lack of accumulated mathematical facts for many children can be detrimental to understanding even the simplest mathematical truths.

On the other hand, considering the cognitive activity of schoolchildren in the study of mathematics in the aspect of subjective belief in the truth of mathematical statements, these latter in terms of their evidence can be perceived as immutable facts or in any way be taken for granted. At the same time, the belief in the truth of mathematical statements can be true or false and have various grounds. According to Bertrand Russell, "advanced science is built on elementary science, and elementary science is built on common sense," and further "Knowledge of general connections between facts is more different than is usually supposed from knowledge of particular facts" (Russel, 1948, pp. 513–514).

Thus, the question of cognition in school mathematical education can be reduced in some way to the question of the degree of evidence of the material being studied. Consequently, such concepts as fact, faith, truth and cognition need a separate consideration in order to exclude the risks of confusion in the methods of teaching mathematics.

Research Questions

In studies of methodological nature, the problem of cognition in obtaining mathematical education at all levels is considered mainly in the aspect of the logical skills of "evidence". "All the primary provisions of the philosophy of mathematical education are based on the formation of practical skills in the education of culture and the" discipline "of thinking. Due to this cognitive priority, students and students have a conscious distinction between the concepts "truth" and "lie", "proven" and "hypothetical" (Yerovenko, 2015, p. 101). In our study, logical imperatives are considered as one of the means of persuasiveness, whose role at the initial stages of learning (or studying a new theory) is negligible, but it increases as the student progresses in the study of mathematics. The focus of the research, therefore, is on the links between the success / poor progress of schoolchildren with the teaching methodology of mathematics concerning the role of facts, faith and truth in the cognitive activity of schoolchildren.

Therefore, for productive cognitive mathematical activity it is necessary: (1) to understand the meanings of words, including mathematical terms, and sentences, and (2) to understand the truth and falsity of statements. With respect to school mathematics, the understanding of words is provided by visual representations in the process of accumulating facts, and the understanding of sentences is by understanding words and understanding logical connectives. However, if the meaning of sentences, generally speaking, does not need specific experience, then the meanings of the terms entering into them should be obtained from experience. Therefore, the cognitive activity of the child should begin with an acquaintance with the facts. The facts accumulate as impressions as a result of the objective activity of children. For example, for a pupil of lower grades the equality of the opposite sides of a rectangle, or the equality of the angles of a regular triangle, or the permutation law of addition, are the same facts as, for example, the fact that this pupil was born of a certain number of such and such a month of that year.

Further, the cognitive activity of a schoolchild in teaching mathematics is based on the belief in the truth of mathematical statements. This faith is acquired through the generalization of facts (inductively) or logical deduction (deductive method) and manifests itself in training activities or in a sense of consent. For example, a student may believe that the sum of the angles of a triangle is 180°. Based on this belief, he can conclude that, for example, all the angles of a regular triangle are equal to 60, and be sure that the utterance of the phrase "the sum of the angles of a triangle is 180" in the presence of the teacher will make a last impression on the latter. Many training tasks with the question: "Is it true?" require only a faith to receive a response.

Finally, the belief in the truth or falsity of mathematical statements for students can be twofold. Often students learn the definitions or formulations of theorems, etc. and utter them, not paying attention to the meaning of the words entering into them. In this case, we will talk about the "verbal" belief in the truth of mathematical statements. If the "set of words" for the student is less important than the content of the statement, we will call such a belief "meaningful".

Thus, in analyzing cognitive mathematical activity of schoolchildren, we will take into account, first, that students' understanding of the meaning of mathematical suggestions and actions is based on their sensory experience, responsible for the accumulation of mathematical facts, and their linguistic development. Secondly, we will interpret students' belief in the truth of mathematical statements in two different ways — as "verbal" or "content."

Purpose of the Study

The transition to new standards in the world practice of school education is associated with the transition from traditional teaching of mathematics to transferring accents from reproductive (memorization, repetition, etc.) to productive (tasks of an applied nature, experiments, etc.) forms of work of schoolchildren (Li & Leung, 2010, pp. 12-13). Such a large-scale reform of school mathematics education requires increased attention to issues related to the mathematical literacy of students.

In the monitoring of the quality of general education, the PISA (Program for the International Student Assessment), as one of the parameters of the readiness of 15-year-old students for a full-fledged life in modern society, is adopted mathematical literacy, which is defined as follows: "Mathematical literacy is the ability of an individual to formulate, apply and to interpret mathematics in a variety of contexts. It includes mathematical reasoning, the use of mathematical concepts, procedures, facts and tools for describing, explaining and predicting phenomena. It helps people understand the role of mathematics in the world, express well-grounded judgments and make decisions that constructive, active and reflective citizens must take" (Osnovniye resultaty mezhdunarodnogo issledovaniya PISA-2015, 2015).

In this connection, it is of interest to analyze the structure of the mathematical experience of the pupil of the junior classes in the context of the formation on the basis of his mathematical literacy of a graduate of a secondary school. Thus, the goal of the work is to establish those meanings of words, fact, faith, truth and cognition, which may prove useful for clarifying the philosophical and methodological problems associated with the development of the student's mathematical literacy.

Research Methods

The effectiveness of school mathematics education now increasingly depends on the experience of students (Owusu-Mensah, 2016). During the study, we have analyzed cases of poor progress in school mathematics both from our experience and described in scientific and methodical literature: (Baruk, 2014; 2016). Interviewing schoolchildren has shown that some of their mistakes are due to a lack of understanding of the meaning of mathematical terms and, accordingly, of statements that describe mathematical facts. As practice shows, the reason for the poor progress of many students is that for many of those terms, there exist similar or same words in the common language but with different meanings. Children of primary school age tend to use words denoting mathematical terms in another meaning. For example, a child stably admits mistakes in assignments of a geometric nature and, being requested to give an example of intersecting lines, depicts parallel lines, accurately repeating the definition. In this case, the explanation was: "here on this straight line I go (runs a finger along one line from left to right), here on this line Liza walks (runs a finger along the other line from right to left), here we intersect and greet Liza (shows the point between the lines)."

The analysis of written works shows that the mistakes traditionally made by students resulting from the misuse of certain mathematical rules are traditionally common. Among them is confusion in mathematical symbols. Thus, the improper application of the distributive law of multiplication relative to addition to objects that have only an external similarity with the operation of multiplying a number by a sum (Figure 01 ) (Markushevich, 1978, p. 41):

See Full Size >

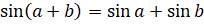
Here you can also include an example from the works of entrants, which became classical at the Faculty of Mathematics of Moscow Pedagogical State University in Soviet times (Figure 02 ):

See Full Size >

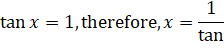
An analysis of the cases of school practice in teaching mathematics shows that some teachers require the exact reproduction of mathematical statements, forbidding even changing the order of words. The argument is simple — "you do not rearrange the words in verse, here and there it is not necessary." Because of this, the corresponding algorithms are perceived by many children as mantras, and children often randomly sort them, like Al-Baba's brother from the fairy tale "Ali Baba and the Forty Thieves", which penetrates the cave, but cannot get out of it, confusing it ("Open sesame" or "Sésame, ouvre-toi") with the names of other plants. Therefore, a calculation for memory, rather than common sense and experience, often leads to gross errors.

The analysis of educational texts makes it possible to reveal gaps in the conceptual apparatus of mathematics courses. Thus, for example, in the presentation of the method of mathematical induction, in some school textbooks there is not even a mention of the important mathematical concept of recursion, which lies at the basis of this exposition (Nikolsky, 2017). Similar omissions are also encountered at earlier stages — when studying the angular division algorithm, when solving systems of linear equations, etc. The missing links deprive reason of clarity, violate the semantic links of the course, unjustifiably strengthen the deductive nature of reasoning in the school course of mathematics and involve the risk of forming a "verbal belief" in the truth of mathematical propositions, sterile from the point of view of productive mathematical activity.

On the other hand, the analysis of positive experience shows that the highest degree of understanding is achieved in the facts perceived by the senses — for example, the "proof" of the equality of the opposite sides of a rectangle for a junior pupil is the measurement and comparison of lengths. The school student, who himself tore off the three corners of the paper triangle and consistently folded them, combining the tops and attaching sides to each other, will receive not only an unfolded corner, but an impression that will not soon be forgotten and will recall this fundamental mathematical fact. Belief in the truth of such a fact is of a substantial nature and, consequently, such a fact can become an instrument of the student's productive mathematical activity.

Findings

As a result of the research, it was revealed that the difficulty of understanding mathematical terms and statements and the belief in the truth of mathematical statements based on verbal conformity to standards can be attributed to the mass difficulties of schoolchildren in solving mathematical problems.

The positive experience of teaching mathematics in the school and teaching students in a pedagogical university, analyzed by us, suggests that both these problems are solved by reviewing the content of school mathematical education. Therefore, it seems reasonable to structure the content of education in relation to some mathematical facts, more precisely speaking, with respect to a system of (possibly excessive) mathematical artefacts specially selected so that the practice of handling them allows the child to accumulate the experience necessary for understanding mathematical terms and statements. For this, it is necessary to "legalize" the experimental method in teaching mathematics

Conclusion

Cognitive activity in the study of mathematics is subject to objective difficulties. Before the methodology of mathematics is a difficult task, on the one hand, to form in schoolchildren visual representations of mathematical objects that are not perceived by the senses and are not of a public nature. Moreover, students should be convinced of the truth of mathematical statements, that is, statements about the properties of mathematical objects that are not perceived by sense organs and not of a public nature.

Based on the foregoing and the results of earlier studies, it can be hypothesized that the content of school mathematical education should be based on the following basic principles. First, the principle of minimizing the nomenclature of the material being studied serves to ensure that children have enough time to acquire experience and accumulate a variety of mathematical facts - for "observations and generalizations." Secondly, this "maximization of intra-subject connections" is necessary to "clarify the relationship between individual elements and formal structures in general". Third, the "maximization of inter-subject connections" is necessary for working out mathematical algorithms and logical templates in contexts different in content (Sedova, 2018).

Thus, in the methodological system of teaching mathematics, it is advisable to study the cognitive process from the point of view of the degree of obviousness of the terms and statements being studied. To describe this process it is appropriate to use the terms: fact, faith, truth and cognition, treating them as follows: fact is an artefact, the practice of dealing with it allows you to gain the experience necessary for understanding mathematical terms and statements (physical body, graph; etc.); faith is the belief in the truth of mathematical statements, based on understanding (common sense and experience) or on a sense of harmony; in the first case is meaningful, in the second - verbal; truth is the obviousness of mathematical statements; The method of establishing truth can be inductive or deductive at various stages of learning; and, finally, cognition is the process of cognition of mathematics, based on experience: the obvious truths are obtained from the perception and generalization of facts; further they serve as a material for logical conclusions, as the logical constructions become more complex.

A study shows that in engineering and natural science oriented graduate schools, the teachers identify serious gaps in the mathematical background of the students. Filling these gaps requires introducing additional courses into the graduate school program thus reducing the training volume dedicated to the profile subjects. We suggest that paying attention to the philosophic-methodological basics of the education will promote positive shifts in this situation (Samylkina, Sedova, Karakozov, Polikarpov, & Bosova, 2017).

Acknowledgements

The authors thank Dr. Anna Beuchat and Dr. Françoise Villars-Kneubühler, french didactician (Pedagogical Institute of HEP BEJUN, Switzerland) for the information provided, which helped to significantly improve the article. The article has been prepared under the state assignment to the Institute for Strategy of Education Development of the Russian Academy of Education (project No. 27.6122.2017/BCh).

References

1. Baruk, S. (2014). Nombres à compter et à raconter. Paris: PUF.
2. Baruk, S. (2016). Les chiffres ? Même pas peur ! Paris: PUF.
3. Federalniya gosudarstvenniye obrazovatelniye standarty obschego obrazovaniya. (2012, March 01). Retrieved from https://минобрнауки.рф/документы/543 [in Rus].
4. Heath. (n.d.). Eceryman's library Euclid Introduction. Retrieved from http://www-history.mcs.st-andrews.ac.uk/Extras/Everyman_Euclid.html
5. Ivanova, S. (2016). Pedagogicheskiy aspekt vliyaniya infokommunikatsionnyh tehnologiy na obrazovatelnoye prostranstvo. (S. Ivanova, Ed.). Obrazovatel'noe prostranstvo v informatsionnuyu epokhu (EEIA), 93-99 [in Rus].
6. Li, Y., & Leung, F. (2010). Reforms and issues in school mathematics in East Asia: sharing and understanding mathematics education policies and practices. Rotterdam, Boston: Sense Publishers.
7. Markushevich, A. (1978). Ob ocherednyh zadachah prepodavaniya matematiki v shkole . In Na putyah obnovleniya shkolnogo kursa matematiki (Vols. 29-48). Moskva: Prosvescheniye [in Rus].
8. Nikolsky, S. P. (2017). Algebra i nachala matematicheskogo analiza. 10 klass: uchebnik dlya obscheobrazovatelnyh uchrezhdeniy: bazoviy i profilniy urovni . Moskva: Prosvescheniye [in Rus].
9. Osnovniye resultaty mezhdunarodnogo issledovaniya PISA-2015. (2015). Retrieved from http://36edu.ru/DocLib3/Docs/PISA2015.pdf [in Rus].
10. Owusu-Mensah, J. (2016). Improving the Pedagogical Content Knowledge (PCK) of Mathematics Teachers to Enhance Student Learning and Understanding. IOSR Journal of MAthematics (IOSR-JM), 12, 66-70.
11. Philosofsko-entsiklopedicheskiy slovar. (2010). Retrieved from https://dic.academic.ru/dic.nsf/enc_philosophy/944 [in Rus].
12. Russel, B. (1948). Human knowledge, its scope and limits. London: George Allen and Unwin.
13. Samylkina, N., Sedova, E., Karakozov, S., Polikarpov, S., & Bosova, L. (2017). Problems of school mathematical education through the eyes of teachers and lecturers of higher education institutions: the results of the polls. "Matematika v shkole" ("Mathematics in school"), 2, 36-44 [in Rus].
14. Sedova, E. (2018). Soderzhaniye uchebnogo predmeta «Matematika» v edinstve komponentov kultury i struktury lichnosti . Otechestvennaya i zarubezhnaya pedagogika, 1(47), 143-168 [in Rus].
15. Yerovenko, V. (2015). Philosophy of Dewey education . Belruskaya Dumka, 10, 98-102 [in Rus].