Pedagogical Integration As The Method Of Constructing Cross-Curriculum Modules Of Training Courses

Abstract

The authors of the article present the significance of cross-curriculum modules in Russia and abroad in obtaining a new quality of education: a holistic perception of the world, the assimilation of universal educational activities, meta-subject competencies. The possibilities of pedagogical integration in the formation of cross-curriculum modules of physics and computer science have been analyzed. The intercross-curriculum module as a didactic superstructure over the learning subjects necessary for the formation of meta-subject competencies is determined. The list of cross-curriculum modules of physics and computer science for general education, obtained on the basis of the method of inter-structural integration - the integration of methods and means of computer science with the content of the course of physics has been provided. The following cross-curriculum modules are shown: "Modeling in physics" and "Tabular information model of the domain" Dynamics", "Solving tasks on the laws of conservation and momentum of energy using the computer ","Creating algorithms and spreadsheets of oscillatory motion", "Creating a website layout on topic "Atomic and nuclear physics". The content of the cross-curriculum module "Graphical Information Models of Mechanical Motion" is revealed. Examples of graphic information models of mechanical motion and tasks necessary for their learning by students are provided. Methodical possibilities of inclusion of cross-curriculum modules in the system of teaching physics and computer science in general education are explained. It is shown how the study of these modules leads to the formation of meta-subject competencies in students, which proves the advantages of integrated modules over traditional teaching.

Keywords:

Introduction

Starting from 2010, the Federal State Educational Standard for Basic General Education (FSES), among other requirements, establishes the formation of universal training activities (UTA), meta-subject competencies and expertise. The basic educational programme, according to FSES, should contain "... the description of the concepts, functions, structure and characteristics of the UTA (personal, regulative, cognitive and communicative) and their connection with the content of separate academic subjects, extracurricular activities, and the position of separate components of universal educational activities in the structure of educational activities " (Federal State Educational Standard of Basic General Education, 2010). The formation of such educational elements exceeds the educational potential of a single academic discipline. The formation of meta-subject competencies in terms of integrated courses or cross-curriculum training modules is considered the most productive.

Integrated courses and cross-curriculum modules are quite common in Russia and abroad. In Russia, such courses are created on different integrating foundations: global problems of the present ("Ecology"), the subject of study of a number of sciences ("Environment", "Natural Science"), complex phenomena ("Synergetics"), general scientific theory ("Electrical Engineering") and etc. The goals of these courses are the formation of modern holistic thinking, scientific outlook, meta-subject competencies.

Foreign integrated courses are created in terms of the globalization of education to form its new quality. It has been proven that cross-curriculum courses contribute to the development of cross-curriculum thinking among students (Pike & Selby, 1995; Тye, 2003). For example, the module "International Education", the subject of which provides a new quality of knowledge, contributes to a holistic perception of the world, assimilation of European competences has been created (Grzybowski, 2008).

In our work, we will deal with the construction of cross-curriculum modules of physics and computer science based on the method of pedagogical integration. "Pedagogical integration is the restoration in the process of cognition of the naturally existing integrity of the object - an object, event, phenomenon or process, separated by a description in different sciences" (Federal'nyy gosudarstvennyy obrazovatel'nyy standart osnovnogo obshchego obrazovaniya, 2014).

Pedagogical integration is a kind of scientific integration, which is carried out within the framework of pedagogical theory and practice [1, p.15]. The works of many outstanding scientists - didacticians and methodologists in the field of specific educational disciplines, in particular, physics and computer science (Bezrukova, 1990; Chapaev, 1992) are devoted to the pedagogical integration. The main ideas of scientific research include highlighting basic opportunities for the integration of academic disciplines based on their methodological foundations. Training courses with different integrity levels, including cross-curriculum modules are created by integrating academic disciplines.

The problem of developing cross-curriculum modules of physics and computer science remains relevant today. Solving this problem contributes to the formation of universal learning activities, meta-subject competencies and the application of IT technologies in all spheres of the future adult life of a pupil.

Problem Statement

There is a contradiction between the requirements of the FSES to the formation of meta-subject competencies and the absence of cross-curriculum modules of academic disciplines, within which these competencies could be successfully formed.

The cross-curriculum module is a didactic superstructure over the subjects which is necessary for meta-subject competencies formation. The development and implementation of cross-curriculum modules should, on the one hand, provide the implementation of FSES requirements, and on the other hand, be basedupon integral didactic capabilities of specific subjects. Each cross-curriculum module should provide the development of at least one meta-subject competence and respective cross-curriculum knowledge and skills.

We have chosen the method of pedagogical integration for constructing a cross-curriculum module of physics and computer science, since it enables us to restore the unity and integrity of the objects of study by selecting individual subject elements.

Research Questions

In our study, we searched for answers to the questions:

• What is the content, and what are the possibilities of pedagogical integration of school subjects?

• What are the advantages of modular integration of physics and computer science?

• What technological steps are required for cross-curriculum modules formation?

• How many cross-curriculum modules of physics and computer science should be included for grade 9?

• How to form the content of a specific cross-curriculum module of physics and computer science (on the example of the module "Graphical and informational models of mechanical motion")?

Purpose of the Study

Formation and justification of cross-curriculum modules of physics and computer science, which allow to form subject and meta-subject knowledge and skills of the above disciplines, based on pedagogical integration method.

Research Methods

The methods applied in our study are:

• method of pedagogical integration for construction of cross-curriculum modules of training courses in physics and computer science;

• methods of analysis and synthesis for identification of the content, capabilities and types of pedagogical integration of academic subjects, in particular - the integration of physics and computer science;

• the method of generalization and concretization is used to justify the stages of creating cross-curriculum modules of academic disciplines;

• the method of pedagogical experiment is used to test the quality of students' mastering subject and meta-subject knowledge and skills in the study of cross-curriculum modules by schoolchildren.

Findings

As a result of the research, it was revealed that the difficulty of understanding mathematical terms and statements and the belief in the truth of mathematical statements based on verbal conformity to standards can be attributed to the mass difficulties of schoolchildren in solving mathematical problems.

The positive experience of teaching mathematics in the school and teaching students in a pedagogical university, analyzed by us, suggests that both these problems are solved by reviewing the content of school mathematical education. Therefore, it seems reasonable to structure the content of education in relation to some mathematical facts, more precisely speaking, with respect to a system of (possibly excessive) mathematical artifacts specially selected so that the practice of handling them allows the child to accumulate the experience necessary for understanding mathematical terms and statements. For this, it is necessary to "legalize" the experimental method in teaching mathematics.

Russian scientists distinguish three levels of pedagogical integration: the educational process, the content of education and the content of a particular subject (Bezrukova, 1990). The main feature of the content-based subject level of integration is the fusion of elements of different subjects (knowledge, skills, etc.) in one synthesized course, which lose their structural independence in the integrated academic subject.

It is substantiated that educational subjects with a common object or theoretical concept, for example, natural science disciplines: physics, chemistry, biology, are well integrated. They have a common object of research - nature and general theoretical concepts - molecular-kinetic theory, electron theory of matter. The leading role in this integration belongs to physics, since many chemical and biological laws, phenomena and processes are explained on the basis of physical laws.

Views on cross-curriculum integration have in many ways been expanded by the concepts of intra-structural, inter-structural and external integration. (Chapaev, 1992). Academic disciplines include didactic elements - what students should learn: knowledge, skills, while at the present time it is competences. Intra-structural integration involves the integration of the same elements from different disciplines, for example, knowledge with knowledge, skills with skills, etc. Inter-structural integration involves the integration of different elements from different disciplines, for example, knowledge with skills, etc. External integration means the combination of skills with organizational forms, or skills with teaching methods. As a result of cross-curriculum integration, all components of the content of objects are transformed or assimilated. In other words, a different degree of integrity can be achieved.

Levels of integration of cross-curriculum modules for disciplines from different blocks will be lower, for example, natural science and polytechnics. Let us, as an example, consider the possibilities and results of integrating physics and computer science. Physics and computer science have different objects. Physics is the science of inanimate nature, in which the most general laws of nature are studied. Computer science is a science that systematizes the methods of creating, storing, processing and transferring information by means of computer technology, as well as the principles of the functioning of these tools and the methods of managing them.

The object of physics is nature; the object of computer science is information. These disciplines have different methods of research: in physics - observation and experiment, in computer science - methods of working with information (accumulation, storage, processing, transmission, etc.). In this respect, the methods of these sciences are different.

It is clear that these sciences do not have shared theoretical concepts. Physical science is based upon four fundamental physical theories: classical mechanics, statistical physics, classical electrodynamics and quantum physics. The theoretical basis of computer science is a group of fundamental sciences such as: information theory, theory of algorithms, mathematical logic, theory of formal languages and grammars, combinatorial analysis, etc. Thus, these sciences cannot form cross-curriculum modules with a high degree of integrity.

The only exception to the entire computer science course is the study of physical media devices and the fundamentals of computer technology. In different classes this material is represented in one or several paragraphs of textbooks Computer science and ICT. The physical foundations of computer technology are studied throughout all years of computer science, but at different levels of content. In this topic, a schematic diagram of the computer and peripheral devices are presented as electrical devices. Their ability to receive, process, transform and transmit light, sound, electrical and magnetic signals - physical media - is explained. Integration of this topic with the topics of the physics course: "Laws of direct current", "Magnetic phenomena", "Light phenomena" (8-th grade), "Sound vibrations and waves" (9-th grade) should have the highest degree.

However, it is generally accepted that the methods and means of computer science reach the end user as information technology (IT). The term "information technology" became widely used in the late 70's - early 80's due to the development of electronic technology, which allowed to quickly and efficiently process a wide range of information. According to UNESCO definition, "Information technology is a complex of interrelated scientific, technological, engineering disciplines, which study methods of effective labor organization of people engaged in processing and storing information; computing techniques and methods of organization and interaction with people and production machinery, their practical applications, as well as related social, economic and cultural issues " (Definition of information technologies adopted by UNESCO).

The above-mentioned possibilities for integrating sciences physics and computer science are also characteristic of the corresponding academic disciplines. In terms of pedagogical integration, these subjects are not related, thus their external integration is possible, suggesting the transfer of methods and means of one discipline to another. In practice, there is a transfer of methods, technologies and means of computer science to the content area of the educational subject physics, which makes it possible to learn physical concepts and laws more successfully or a transfer of teaching aids, mainly physical tasks, to the informative part of computer science, which allows students to successfully form skills and competencies in the information technology. This approach was previously considered in our works (Mashinyan & Kochergina, 2017a, 2017b). When you combine the methods of one discipline with the content of the other, the inter-structural integration is realized.

The development of cross-curriculum modules involves modeling simultaneous (or close-in-time) learning of related topics in two or more subject areas on the basis of a single module content, agreed methodology, and considering the interpenetration of tasks into each subject area.

Stages of creating across-curriculum module:

• Identification the FSES requirements, the implementation of which is complicated in the context of a separate study of physics and computer science.

• Determining the content of the module, the learning of which is necessary for the development of FSES meta-subject competencies.

• Methodical development of module implementation.

In accordance with the above stages, a list of cross-curriculum physics and computer science modules for grade 9 has been constructed (table).

The introduction of cross-curriculum modules involves solving a number of fundamental issues. First - at the expense of what hours and in the study of what topics is it possible to implement the suggested module? Second, is there a need for the time correction of the study of the subject modules for a coordinated study of the cross-curriculum module? Third - how in the methodical plan to provide the fulfilment of the principle of complementarity in the process of implementation of the cross-curriculum module in terms of separate subjects (physics and computer science)? The fourth is how to provide technological correction of the results of studying the cross-curriculum module in two academic subjects? Fifth - what is the final result of studying the cross-curriculum module for physics and for computer science?

We will try to respond to all the questions. Cross-curriculum modules of physics and computer science (there are 7 in total) can be implemented at the expense of the hours devoted to revision and summarizing knowledge in each academic subject. This is quite realistic, since most school teachers teach both physics and computer science. Another possible way of cross-curriculum modules implementation is making them part of elective courses. Elective courses are an integral component of the educational process of the modern school, especially in lyceums.

As can be seen from Table 1 , the topics of physics and computer science courses are studied almost concurrently during the school year. Therefore, there is no need for the correction of time of the study of subject modules. In the methodical terms, the principle of complementarity is already fulfilled when the topics of the physics and computer science courses are coordinated. Technological correction of the results of the study of the cross-curriculum module can be performed using inverse connection of two subjects, during diagnostic work at intermediate stages. Based on diagnostic results, corrections and additions are made to the content and methodology of the cross-curriculum module. The formation of the meta-subject competencies specified in the Federal state educational standard is considered as the final result of the study of the cross-curriculum module for physics and computer science.

Let us consider an example of the cross-curriculum module of physics and computer science using the module "Graphical and informational models of mechanical motion" for the 9th form of the general education school: In the process of studying this module, students learn the basic concepts of computer science and physics, meta-subject competencies, including knowledge and skills.

Basic concepts of computer science: scheme, map, drawing, graphic, diagram, graph, network, tree.

Basic concepts of physics: material point, coordinate system, reference frame, trajectory, path, displacement, speed, uniform motion, uneven movement, acceleration, uniformly accelerated motion, laws of velocity and displacement change at uniformly accelerated motion, uniform motion along the circumference.

Basic meta-project concepts: modeling, formalization.

Meta-project skills: the ability to build graphic information models in the study of mechanical motion.

The main methodological idea is to study the mechanical movement using all graphic information models, concentrating the students' attention on the content of both physical and computer science concepts, generate in students the ability to build graphic information models.

The application of modeling in the teaching of natural sciences is widely used in foreign schools (Afzal, Safdar & Ambreen 2015; Gaidule & Heidingers, 2015; Wee & Leong, 2015), especially when organizing problem training (Ageorges, Bacila, Poutot & Blandin, 2014; Kipkorir, 2015; Zeitoun & Hajo, 2015; Schütte & Köller, 2015).

By the time of training in the 9th form, students have a conception of the simplest graphic models: a map a geographical or topographic map as an example, a drawing, an exact picture of technical details, various schemes, as less accurate than the drawing examples.

The position of material points, the movement of the body as a segment that connects its initial and final position, the trajectory of the body's movement, the path travelled can be shown on a simple geographical map. To form meta-subject skills, the following tasks are offered to students:

1. The plane is flying from Moscow to Vladivostok with a landing in Yakutsk. Draw on the map of the Russian Federation the trajectory and vector of the movement of the plane. Given the scale of the map, determine the displacement module and the path of the aircraft.

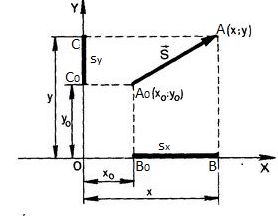
2. Build a flat XOY reference system in the graphic editor. Depict the displacement of a material point from A (2.3) to B (5.6) in it. Construct a displacement vector, find the projections of this vector on the axis OX and OY. Find the modulus of the displacement vector. Perform this task when moving a material point from A (7, 8) to B (1, 1).

To illustrate the concepts of displacement, projection of movement on a computer in a given reference system, a drawing is performed (Fig. 1).

See Full Size >

At the very beginning of the physics course students should learn how to build schemes. A scheme or schematic drawing reflects the basic concepts and the connections between them at a qualitative level. The diagram shows the physical quantities in the form of vectors, their location in space is taken into account. Particularly essential are the schemes in the study of physical phenomena, the derivation of physical laws and the solution of physical tasks.

Skills formation in constructing schemes is repeatedly worked out when solving physical tasks. The diagram (a schematic drawing of the condition and requirements of the physical task) is its simplest model. Without the use of schemes, a physical task, especially with a high degree of difficulty, cannot be solved.

Graphs are more complex models of physical phenomena that reflect the connections between physical quantities. Reading and constructing graphs is the most important polytechnical, therefore, cross-curriculum skill. For example, the figure shows a graph of the dependence of the projection of velocity on time during uniformly accelerated motion (Figure 2 ):

See Full Size >

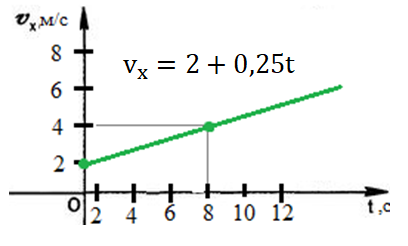
Graphs are used to derive physical laws (Figure 3 ). For example, the graph of the dependence of speed on time during uniformly accelerated motion:

$$v_x=v_{0x}+a_{x}t$$

is used to derive the equation of uniformly accelerated motion:

$$s_x=v_{0x}t+\frac{a_x{t}^2}{2}$$

See Full Size >

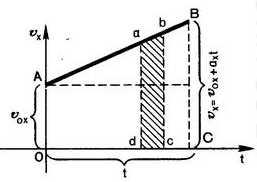
The geometric meaning of the area of the figure located under the graph of the dependence of the projection of velocity on time is the projection of the displacement.

To create the skills for building graphics students get tasks:

1. In the coordinate system, plot the velocity versus time curves:

v = 5; v = 1 + 2t; v = 10 - 5t.

2. Describe each of these types of movement.

In the coordinate system, plot the motion graphs:

x = 5 + 3t; x = 2 + 3t + t2.

What kinds of movement are these?

A diagram is a kind of graphical information model that reflects the quantitative relationships between homogeneous objects. There are the following types of diagrams: columnar, linear, with regions, circular, XY graph, radial, and also point, bubble, speedometer, columnar-linear, pyramid.

In general education physics, all the considered types of diagrams should be applied. To learn the concept of the diagram and the ability to build them, students get tasks:

• In the graphical editor, draw a diagram comparing the speeds of the pedestrian, bicyclist, car, airplane and missile movement. Show in the diagram the approximate values of the speeds of movement of these bodies.

• Using a point diagram of the dependence of the path on time with uniformly accelerated motion with zero initial velocity, formulate the regularity of this type of movement.

Another kind of model: graph. The graph consists of vertices connected by lines-ribs. The vertices of the graph are represented by circles, ovals, dots, rectangles, etc. The objects are represented as the vertices of the graph, and the links are represented as its edges.

A graph is called weighted if its vertices or edges are characterized by some additional information - weights of vertices or edges. For example, the figure can depict the cities and the distances between them in kilometers, the relationship between physical quantities in physical laws.

Basic concepts of graphs: a chain and a cycle. A chain is a path along the vertices and edges of a graph into which any edge of the graph enters no more than once. A cycle is a chain whose initial and final vertices coincide. The graph model has been effectively used in physics for a very long time. For example, a network depicting a graph with a cycle is used to represent any cyclic process (uniform motion of a material point along a circle).

A tree is a graph without cycles - it is used to establish a hierarchy of physical concepts. Thus, all kinds of mechanical motion and the connection between them can be represented as a graph-tree (Fig. 4)

See Full Size >

To learn the concept of graph and the ability to construct graphs, following assignments are offered to students:

• Build a graph on the computer for the concepts of uniformly accelerated motion. Describe the connections between concepts.

• Construct a graph that reflects the relationship between the angular and linear characteristics of the uniform motion of a material point along the circumference.

The pedagogical experiment on the students' acquiring the knowledge of subject and skills in physics and computer science, as well as meta-subject knowledge and skills related to the study of integrated modules, was conducted in the schools of Moscow - the experimental sites of the Institute for the Development of Education during 2016-2018. The results of the formation of the subject knowledge and skills in physics and computer science, meta-subject knowledge in experimental and control classes convincingly prove the advantages of implementing integrated modules.

Conclusion

To summarize, the research that was conducted shows the evidence of both similarities and differences among the employers/media professionals’ versus higher education professors’ versus students’ understanding of modernizing the current journalist education process. According to the employers, the young journalists’ lack of applicable skills needs to be compensated by expanding the types of hands-on training, which should focus on new multimedia specializations within the journalist profession.

References

1. Afzal, M., Safdar, A. & Ambreen, M. (2015). Teachers Perceptions and Needs towards the Use of E-Learning in Teaching of Physics at Secondary Level. American Journal of Educational Research. Vol. 3 (8). pp. 1045-1051. DOI: 10.12691/education-3-8-16
2. Ageorges, P., Bacila, A., Poutot, G. & Blandin, B. (2014). Some Lessons from a 3-Year Experiment of Problem-Based Learning in Physics in a French School of Engineering. American Journal of Educational Research. Vol. 2 (8). pp. 564-567. DOI: 10.12691/education-2-8-1
3. Bezrukova, V.S. (1990). Pedagogicheskaya integratsiya: sushchnost', sostav, mekhanizmy realizatsii: Integratsionnye protsessy v pedagogicheskoy teorii i praktike. Sverdlovsk: SIPI, pp. 5-26.
4. Chapaev, N.K. (1992). Integratsiya pedagogicheskogo i tekhnicheskogo znaniya v pedagogike proftekhobrazovaniya. Ekaterinburg: SIPI, 224 p.
5. Federal State Educational Standard of Basic General Education. 2010. Retrivied from: http://schulen36.ucoz.ru/Obrazov_prog/2.1-2.2-programma_uud.pdf
6. Federal'nyy gosudarstvennyy obrazovatel'nyy standart osnovnogo obshchego obrazovaniya. (2014). Chto takoe pedagogicheskaya integratsiya? Retrieved from: http://gigabaza.ru/doc/88810.html
7. Gaidule, A. & Heidingers, U. (2015). The Use of Associative Images (models) for the Development of Comprehension in Sciences Education. American Journal of Educational Research. Vol. 3(10), pp. 1305-1310. DOI: 10.12691/education-3-10-15
8. Grzybowski, P. (2008). Edukacja europejska: od wielokulturowosci do miedzykulturowosci. Warszawa. 120 р.
9. Kipkorir, R.N. (2015). Influence of CBL Methods on Secondary School Physically Handicapped Students’ Academic Achievement in Mathematics in Kenya. American Journal of Educational Research. Vol. 3 (9). pp.1122-1132. DOI: 10.12691/education-3-9-9
10. Mashinyan, A.A., Kochergina, N.V. (2017a). Metodicheskie osnovy sozdaniya demonstratsionno-informatsionnyh kompleksov kursa fiziki: metod. posobie dlya uchiteley shkol i studentov pedvuzov. Moskva: Pero. 82 p.
11. Mashinyan, A.A., Kochergina, N.V. (2017b). Tekhnologii obucheniya resheniyu fizicheskih zadach v usloviyah sovremennoy informatsionnoy sredy. Mir nauki, kul'tury, obrazovaniya. № 5. pp. 167-171.
12. Pike, G., Selby, D. (1995). Reconnecting: from national to global curriculum. Guilford: World Wide Fund for Nature UK. 80 p.
13. Schütte, K, Köller, O. (2015). Discover, Understand, Implement, and Transfer: Effectiveness of an intervention programme to motivate students for science. American Journal of Educational Research. Vol. 3 (3), pp. 268-275. DOI: 10.12691/education-3-10-15
14. Wee, L.K., Leong, T.K. (2015). Video analysis and modeling performance task to promote becoming like scientists in classrooms. American Journal of Educational Research. Vol.3 (2). pp. 197-207. DOI: 10.12691/education-3-2-13
15. Zeitoun, S., Hajo, Z. (2015). Investigating the science process skills in cycle 3 national science textbooks in lebanon. American Journal of Educational Research. Vol. 3 (3), pp. 268-275. DOI: 10.12691/education-3-3-3
16. Тye, K.A. (2003). Global education as a Worldwide Movement. Phi Delta Kappan. Vol. 85, № 2. pp. 102-117.