Abstract
The aspects of the multi-objective optimization in the development of the SVM classifiers has been considered. The NSGA-II has been used to provide the simultaneous search for the optimal values of the classification quality indicators chosen from the such classification quality indicators as total accuracy, completeness, sensitivity, specificity,
-measure and, also, the supports vectors number. The program which allows comparing the SVM classifiers and the values of the classification quality indicators found by the NSGA-II and choose the best ones has been developed. Approbation of the developed program on the real datasets taken from the Statlog project and the UCI Machine Learning Repository has confirmed the efficiency of the developed tools of the data analysis with application of various combinations of the classification quality indicators. Also, the program has been applied to predict the success of passing of the unified state examination (USE) on "Russian language" and "Mathematics" disciplines, which are obligatory to delivery for obtaining the certificate about the secondary education. A herewith, the poll results of pupils of the graduation classes of school, which reflect the different personal features, family features, etc., before passing the USE were used to create the training dataset. The analysis of the experimental results confirms the efficiency of the SVM classifiers for the prediction problem solution of the USE success on "Russian language" and "Mathematics" disciplines.
Keywords: SVM classifiergenetic algorithmmulti-objective optimizationNSGA-I
Introduction
In the data mining problems list, there is a special place for the classification problem, the solution of which is necessary, for example, in the credit scoring area, in the field of medical diagnostics, in the area of text categorization, for the face identification etc. A good solution to this problem is also in demand in the educational sphere. In recent years, in various educational institutions students are actively involved in various polls and tests, including the use of the widely approved methods to review their intellectual level, individual psychological characteristics, specialization profiling, etc.
For example, the diagnostics problem's solution of the readiness of the first-year students for continuation of training in higher education institution or college on the base of analysis of the students’s psychological characteristics as subjects of the educational and professional activity has an essential interest.
A herewith, to review the first-year students, the motivational component diagnostics can be performed (Atkinson, 1981; Zelick, 2007; Bye & Sandal, 2016). Also, the cognitive component can be inspected by R. Amthauer's intelligence test (Weiss, 1975), which allows evaluating the verbal, mathematical and spatial intelligence. Besides, the personality component diagnostics can be performed by means of the five-factor personal questionnaire, which allows evaluating the expression degrees of personal qualities on the base of five factors (introversion – extroversion, emotion stability – neuroticism, non-perception of new information – perception, non-concentration – consciousness, hostility – goodwill) (Hege et al., 2016).
Another actual data analysis problem in the educational sphere is the diagnostics problem of the individuals’ prepare to pass the final state attestation. To solve this problem, in particular, it is necessary to analyze the data which consolidates information on individual self-reviewing, as well as information on his immediate environment and the habitat comfort. A herewith, the classification problem can be solved as the problem with the purpose of predicting whether the result of the final state attestation will be high-scoring, or the problem of predicting of the exam's scores sum of the final state attestation.
Obviously, the results of polls and tests accumulated in large amount can be used to extract the additional hidden information, in particular, to identify the certain cause-effect relationships and interrelations in the context of the individual's personal diagnostics, and to develop the classifiers and to construct the regression models for forecasting’s purpose of certain events.
Nowadays, the various algorithmic tools are used to solve the problems which require to make the data analysis. The most famous algorithmic tools are the following: linear and logistic regressions, Bayesian classifier, decision trees, decision rules, neural networks, the nearest k-neighbors algorithm (k-Nearest Neighbors Algorithm), support vector machine algorithm (SVM algorithm), and so on.
A herewith, from the point of view of the presented possibilities and the undeniable advantages declared in the works of the scientific community, in the context of solving the data analysis problems in the educational sphere, the most promising is the use of the SVM algorithm, possibly in combination with other intelligent data analysis algorithms.
Problem Statement
The proposed article examines the problem of the individuals’ diagnostics who are preparing to pass the final state attestation. A herewith, the forecasting of the attestation success in a particular discipline must be carried out taking into account the a priori data consolidating the individual self-review information, as well as information on his The proposed article examines the problem of the individuals’ diagnostics who are preparing to pass the final state attestation immediate environment and habitat comfort.
It is possible to develop (train) the classifier targeted on applying it for the classification of new individuals, if the training dataset containing a priori information about individuals and the results of their passing of the final state attestation is available.
To solve this problem, it is proposed to implement the development of the SVM classifier (Vapnik et al.,, 1998) based on the multi-objective optimization genetic algorithm, called the NSGA-II, which is one of the most effective algorithms for the multi-objective optimization (Srinivas & Deb, 1994; Deb et al., 2002).
Using the SVM algorithm to develop the SVM classifier in order to predict, whether the result of the final state attestation will be high or not, can be justified by the fact that in the long term it is planned to apply it for the regression model (Gunn, 1998) development aimed at predicting the sum of scores of the final state attestation.
The use of the NSGA-II can be justified by the necessity to involve in the training of the SVM classifier and the classification results’ analysis the classification quality indicators such as total accuracy, sensitivity, specification, etc., in order to select the most effective SVM classifier and obtain the most appropriate classification results for new individuals.
Research Questions
In the offered article the following research questions are considered:
the problem of the multi-objective optimization in the context of the solution of the SVM classifier development problem;
the problem of the software development on the base of the SVM algorithm and the multi- objective genetic algorithm known as the NSGA-II;
the problem of the data analysis in the educational sphere with application of the developed software taking into account various combinations of the classification quality indicators in the context of the solution of the forecasting problem of the passing's success of the final state attestation by the individual.
Purpose of the Study
The research objective is the software development which must provide the classifier training on the base of the SVM algorithm and the multi-objective genetic algorithm known as the NSGA-II. This software must allow to make the analysis of the results of classifier training at various combinations of the chosen classification quality indicators in the context of the solution of the forecasting problem of the passing's success of the final state attestation by the individual for some discipline on the base of the aprioristic data consolidating in themselves the information on self-diagnostics of the individual and, also, the data on his immediate environment and the habitat comfort.
Research Methods
Support Vectors Machine Algorithm
SVM algorithm allows solving the problems of binary classification using the hyperplane to separate the classes marked by "+1" and "–1". A herewith, it is necessary built to two parallel hyperplanes (which are parallel to the separating hyperplane ) at the maximum distance from each other to form the boundaries of classes.
Let we’ve the linearly separable objects of two classes in some space of characteristics.
Depending on the location of some object relatively the separating hyperplane, this object can be classified according to the classification rule (Vapnik et al., 1998; Demidova et al., 2016; Demidova et al., 2017):
,
where is the scalar product of vectors and , is the perpendicular vector to the separating hyperplane; is the vector of the object’s characteristics; is the distance from the center of coordinates to the separating hyperplane.
The support vectors are the vectors of the characteristics of objects that are located at the closest distance to the parallel hyperplanes and fit to constraint (Vapnik et al., 1998):
,
where is the variable equals to 1 for objects of the class "+1" and equals to –1 for objects of the class "–1".
The distance between the classes boundaries (the width of the separation strip) is defined as follows:
.
To build the SVM classifier it is necessary to find the values of and parameters taking into account the distance between the classes boundaries which must be maximized and the constraint imposed on the support vectors. To perform it, the Lagrange multiplier optimization method is used. As a result, the classification rule transforms into (Vapnik et al., 1998):
.
where
is the number of objects;
is the Lagrange multiplier;
is the
Thus, the SVM algorithm searches for the optimal separation hyperplane for more accurate classification.
In the case of the linear inseparability of classes, it is necessary to use the kernel functions, which provide the linear separability of classes in the space of higher dimension (Vapnik et al., 1998; Gunn, 1998; Demidova et al., 2016; Demidova et al., 2017).
Classification quality indicators
Usually, the classification quality indicators based on the errors of the first and second kind are used to get the classification quality. Depending on the actual and determined by the classifier class, the following issues of solving of the classification problem are possible: True Positive ( ), False Positive ( , Error of the Second Kind), True Negative ( ), False Negative ( , Error of the First Kind) (Demidova et al., 2017).
The most commonly used classification quality indicators are the following:
total accuracy: , where is the number of objects in the dataset;
sensitivity: ;
accuracy: ;
specificity: ;
-measure: .
Since the classification quality indicators are the multi-extremal functions, it is advisible to use the evolutionary optimization algorithms, for example, the genetic optimization algorithm, instead of the classical optimization algorithms.
NSGA-II
Nowadays, various implementations of the genetic algorithms that optimize a single objective function (such called single-objective genetic algorithms) have many applications. At the same time, the multi-objective genetic algorithms that provide the multi-objective (multicriterial) optimization are becoming more and more popular.
The multi-objective optimization is the simultaneous optimization of several objective functions which can be neutral, consistent or contradictory in a given area of definition. The mathematical description of the multi-objective optimization problem can be represented as:
,
Where , is an area of the valid solutions; is the -th objective function; is the number of the objective functions; is the number of characteristics ( ).
It is rationally to use the NSGA-II (Non-dominated Sorting Genetic Algorithm), proposed by K. Deb in 2002 (Deb et al., 2002),, as the multi-objective optimization algorithm. The main advantages of the NSGA-II are the elitism strategy used in it (the best candidates are copied to the next generation) and the support of the variety solutions with taking into account the crowding distance.
The implementation of the NSGA-II can be described by the following steps (Seshardi, 2006).
1. Population initialization.
2. The non-dominated sorting of the solutions candidates which are coded by chromosomes. It assigns to each candidate a rank according to the rule: the non-dominant points will have the rank of 1, which form a first front; the points which are dominated by the first front will have the rank of 2, they form the second front, etc.
3. The condition checking of the algorithm stop (the number of generations is exceeded o the execution time is exceeded). If the condition is not carried out, it is necessary to repeat steps 3 – 7, else it is necessary to stop algorithm.
4. The tournament selection. In the case of binary tournament selection two random candidates are selected and their phenotypes are compared. The candidate with the best value of the fitness functions is chosen as parent.
5. The implementation of the genetic crossing and mutation operators to create new chromosomes.
6. The sorting of the solutions candidates which are coded by chromosomes of population and new chromosomes.
7. The creation of new population on the base of the best solutions (the best chromosomes).
All chromosomes are coded by the values of the classifier model parameters: (the value of the regularization parameter and the value of the Gaussian kernel function parameter).
Each classifier model can be evaluated by the following classification quality indicators: total accuracy, completeness, sensitivity, specificity, -measure. Depending on the problem conditions, the set of the most significant classification indicators is chosen for maximization, in addition, the support vectors number must be minimized.
Findings
The program that find solutions according to the sets of the optimized classification quality indicators and the visualization program were written using the Matlab programming language. The choice of the programming language is conditioned by availability of functions for development of the SVM classifier and the multi-objective optimization functions. Functions written using the Matlab programming language can be integrated as the dynamic libraries into such high-level programming languages as Delphi, C#, Java using the MATLAB Runtime.
The program uses the built-in function fitcsvm.m which provides the SVM classifier development: it searches for optimal values of the parameters and for the separation hyperplane).
The function fitcsvm.m takes the following input parameters: the training dataset consisting of the objects characteristics vectors with their class labels, the selected kernel function, the value of the kernel function parameter, and the value of the regularization parameter.
Besides, the realization of the NSGA-II offered by Aravind Seshadri (Seshardi, 2006) is used. This realization has been adapted to the solution search problem according to the set of the optimized classification quality indicators by means of modification of the creation principles of the fitness functions, change of the initialization operator and generation of the first population taking into account the problem restrictions.
The program accepts the following input data: dataset which is used for development of the SVM classifier, sets of the optimized classification quality indicators (such as total accuracy, sensitivity, accuracy, specificity, -measure, number of support vectors), and the genetic algorithm parameters values. As a result of the execution program, the Pareto-fronts of the solutions are formed and the quality indicators values are displayed for each set of the optimized classification quality indicators.
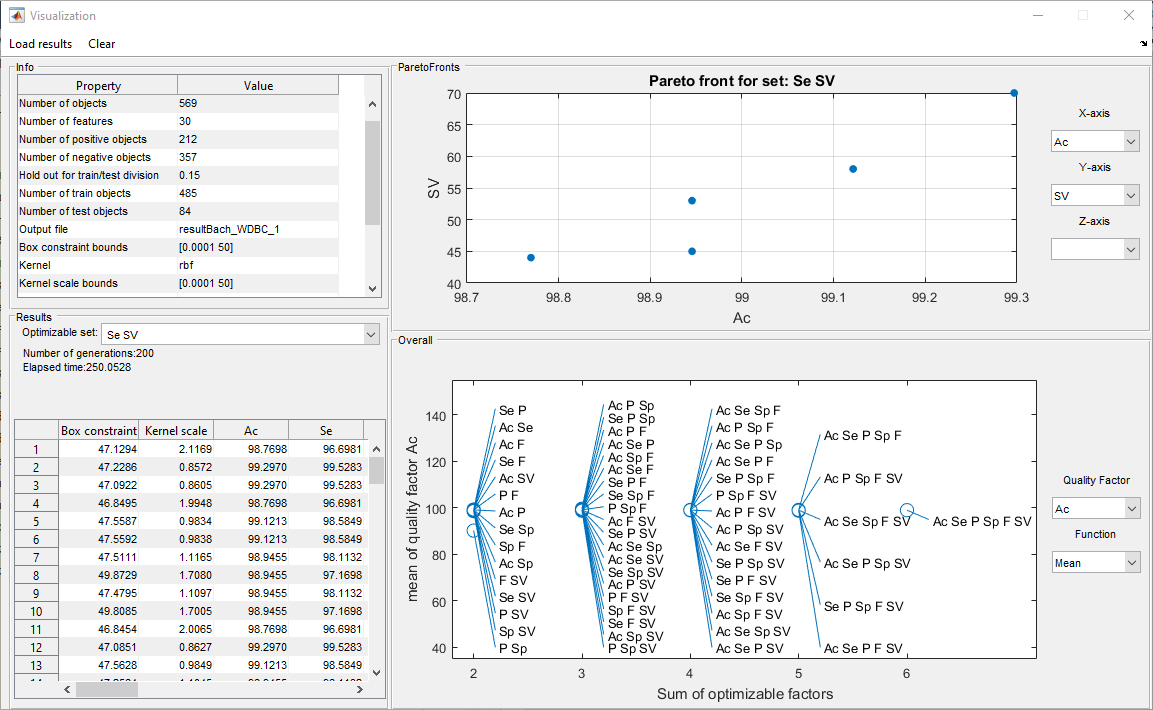
The program interface (Fig.
1. The Info area contains the basic information about the dataset: the number of objects, the number of characteristics, the number of objects of each class.
2. The Results area displays the Pareto front of the found solutions for the selected set of the classification quality indicators, the number of errors of the first and second kind.
3. The ParetoFronts area displays the values of the classification quality indicators for each classifier with the found values of the regularization and the kernel function parameters, which can be displayed graphically as the Pareto front.
4. The Overall area displays the search results for the minimum, average, or maximum value of the selected classification quality indicator for each set of the optimized classification quality indicators.
Approbation of the developed program was made on the real datasets taken from the Statlog project and the UCI Machine Learning Repository which are traditionally used for testing of the developed machine learning algorithms.
Also, the synthesized (model) poll results of 546 pupils of the graduation classes of school before passing the unified state examination (USE) and, also, their test marks in USE on "Russian language" and "Mathematics" disciplines were used to develop the SVM classifiers.
The sections of the questionnaire can be divided into 3 following groups.
1. The general questions (the questions concerning the pupil’s plans after passing the exam; questions about what the pupil considers important for admission; the questions allowing to estimate the pupil's relation to the to the subjects being passed; the questions allowing to estimate the relationship of the pupil with the surrounding people, financial position of family, etc.).
2. The questions connected with the "Russian language" discipline.
3. The questions connected with "Mathematician" discipline.
The USE system means the translation of the primary scores of exam into the test ones which are exposed according to the hundred- score scale as a result of the scaling procedure considering all statistical materials received within the USE of this year. Scaling allows to compare and estimate the level of the pupils’ readiness objectively. The results for admission to educational institutions of the secondary vocational and higher education are provided in the test scores. "Russian language" and "Mathematics" disciplines are obligatory to delivery for obtaining the certificate about the secondary education. A herewith, the minimum thresholds specified in the scores and determined in advance must be overcome.
Taking into account the mentioned above, the data preparation for the training dataset on the base of the poll results of the pupils consists in performance of the following steps.
1. The choice of discipline and installation of the threshold of division into classes in the form of test score of the USE.
2. The formation of the characteristics’ vector for each object (pupil) on the base of his poll’s results in the context of the chosen discipline.
As a result, for two disciplines, "Russian language" and "Mathematics", have been created two training datasets of the identical power (with 546 objects), but with the different number of characteristics: 133 characteristics for "Russian" discipline and 141 characteristics for "Mathematics" discipline that is explained by the different number of questions having direct or indirect relation to the corresponding discipline. A herewith, it was experimentally established that it is expedient to establish the threshold division of classes equals to 80 scores for "Russian language" discipline and 70 scores for "Mathematics" discipline (although it is considered that the work is high-scoring, if it had more than 80 scores). The establishment of such threshold values in the made experiments can be explained with the limited size of the polls’ results and the traditionally lower scores on "Mathematics" discipline (and, as a result, lack of the sufficient number of the high-scoring works).
However, at the chosen variants of the objects (pupils) division into the classes with markers "+1" and "–1" the classes are unbalanced, that is the number of objects of one class (the majority class) considerably exceeds the number of objects of the second class (the minority class) (Table
The average solutions got at the realization of 50 generations of the NSGA-II for population of 50 chromosomes for "Russian language" (Table
It is obvious, that the developed SVM classifiers allow predicting the success of the exam with the high accuracy.
Conclusion
Based on the results of the experimental studies, it is possible to say that the program successfully searches for optimal values of the regularization and the kernel function parameters according to the sets of the optimized classification quality indicators.
The analysis of the received results of the experimental studies confirms the efficiency of the SVM classifiers for the prediction problem solution of the USE success on "Russian language" and "Mathematics" disciplines. A herewith, the expediency of the size increase of the training dataset by means of including in it of the results of the pupils’ polls who have got the high scores of the USE is obvious.
As a subject of the further development of the multi-objective genetic algorithm, it is possible to specify the modification of the genetic operators of the NSGA-II for self-parameterization, the subpopulations concept implementation for more efficient search space exploration, and the use of the hybrid version for the processing and possible improvement of the obtained classification quality results.
Acknowledgments
The reported study was funded by RFBR according to the research project № 17-29-02198.
References
- Atkinson, J.W. (1981). Studying personality in the context of an advanced motivational psychology. American Psychologist, 36, 117-128.
- Bye, H.H., Sandal, G.M. (2016). Applicant Personality and Procedural Justice Perceptions of Group Selection Interviews. Journal of Business and Psychology, 31(4), 569-582.
- Chawla, N., Bowyer, K., Hall, L., Kegelmeyer, W. (2002). SMOTE: Synthetic Minority Over-sampling Technique. Journal of Artificial Intelligence Research, 16, 341-378.
- Deb, K., Pratap, A., Agarwal, S., Meyarivan, T. (2002). A Fast Elitist Multiobjective Genetic Algorithm: NSGA-II, IEEE Transactions on Evolutionary Computation 6(2), 182-197.
- Demidova L., Nikulchev E., Sokolova Y. (2016). Big Data Classification Using the SVM Classifiers with the Modified Particle Swarm Optimization and the SVM Ensembles, International Journal of Advanced Computer Science and Applications, 7(5), 294-312
- Demidova, L., Klyueva, I., Sokolova, Y., Stepanov, N., Tyart, N. (2017). Intellectual Approaches to Improvement Of the Classification Decisions Quality On the Base Of the SVM Classifier. Procedia Computer Science, 103, 222-230.
- Gunn S. R. (1998) Technical report on «Support Vector Machines for Classification and Regression», University of Southhampton.
- Seshardi, A. (2006). Multi-objective optimization using evolutionary algorithm. https://www.mathworks.com/matlabcentral/fileexchange/10429-nsga-ii--a-multi-objective-optimization-algorithm?focused=5130594&tab=example.
- Srinivas, N., Deb, K. (1994). Multiobjective Optimization Using Nondominated Sorting in Genetic Algorithms. Evolutionary Computation, 2(3):221-248.
- Vapnik, V. (1998) Statistical Learning Theory. New York: John Wiley & Sons.
- Weiss, B. (Ed.). (1975). Behavioral toxicology. Vol. 5. Springer.
- Zelick, P.R. (Ed.) (2007). Issues in the Psychology of Motivation. Nova Publishers.
Copyright information

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
About this article
Publication Date
13 December 2017
Article Doi
eBook ISBN
978-1-80296-032-7
Publisher
Future Academy
Volume
33
Print ISBN (optional)
-
Edition Number
1st Edition
Pages
1-481
Subjects
Cognitive theory, educational equipment, educational technology, computer-aided learning (CAL), psycholinguistics
Cite this article as:
Demidova, L. A., Egin, M. M., Mikhailov, A. A., Rusakov, A. M., & Sokolova, Y. S. (2017). SVM-Classification Based On The Multi-Objective Optimization In The Educational Sphere’s Problems. In S. B. Malykh, & E. V. Nikulchev (Eds.), Psychology and Education - ICPE 2017, vol 33. European Proceedings of Social and Behavioural Sciences (pp. 84-94). Future Academy. https://doi.org/10.15405/epsbs.2017.12.9

