Abstract
This article discusses the aspects of application of the different psychodiagnostics tests in the educational sphere, in particular, in the schools and universities, to predict some events. Also, the problem of the results classification of the psychodiagnostics tests of individuals in the educational sphere has been considered. The application of the SVM classification based on the imbalanced datasets to this problem has been discussed. The data imbalance is inherent in the results of many tests, for example, intellectual tests. It is shown that the SMOTE (Synthetic Minority Oversampling Technique) and its modification famous as the bSMOTE (boundary SMOTE) algorithm can be used for the data rebalancing. It allows improving the classification results for the boundary objects. A herewith, the novel approach to the search of the parameters’ values of the bSMOTE algorithm has been analyzed. It allows minimizing the time expenditures for development of the best SVM classifier. It is shown, that the Python toolkids allow accelerating the process of the program development, that can be useful for the problem of the SVM classification based on the imbalanced datasets. The analysis of the experimental results confirms the efficiency of the SVM classification, when it is necessary to predict the assessment of individual on the base of the psychodiagnostics tests' results.
Keywords: Psychodiagnosticstesting techniqueimbalanced dataSVM classifiersamplingbSMOTE algorithm
Introduction
The methods and algorithms of classification and ranking according to the psychological and psychophysiological characteristics are used to determine the individual psychological features of the person's personality. The approaches to classification, based on such methods and algorithms, refer to the field of the psychological science, called the psychodiagnostics (Rapaport et al., 1968; Schafer, 2003).
Educational tests (or tests of achievements) do not belong to psychological, since they are aimed primarily at assessing the degree of mastering of one or another educational material. Nevertheless, historically, the development of psychological tests in many ways influenced the development of tools for assessing knowledge. These areas of research are interrelated, they involved psychologists, so in the psychodiagnostics history one can’t ignore the testing in the field of education, which has been and remains the main consumer of psychological tests.
In the early 20th century, tests for measuring intelligence were recognized as the most important tools of educational psychology. Intellect became a special field of study in educational psychology, and the leader of this direction was E. Thorndike. In 1918, Thorndike formulated the principle on which testing in education should be based. The essence of this principle is that "if something exists, then it exists in a certain amount." Learning is associated with changes in a person. The change is in the difference between the two situations; each of these situations is known to us only by the product produced – manufactured things, spoken words, performed actions, etc. Measuring of these products means determining its quantity in such a way that in the end we will know its value better than before measuring.
The Thorndike's book "Education Psychology" became widely known (Thorndike, 2008) among the psychologists, which described the types of tests which were considered the best for determining success in learning.
The publication of this book marked the emergence of a new field of study, called the educational psychology, in which space the problems of measurement was found too. The development of these problems is the subject of Thorndike's classic work "Introduction to the Theory of Mental and Social Measurements" (Thorndike, 2015). In addition to statistical methods, the principles of constructing tests were discussed in this book.
One of the most practically significant individual psychological features of a person is the integral indicator of the human intellect. To measure this indicator, various types of tests are used, the results of which are applied to predict human behavior in a variety of activity spheres, in particular the short screening test (Rapaport et al., 1968).
The main indicator of this test, allowing to give an integral assessment of intelligence, is the number of correct answers given in 15 minutes (the standard time of the test). The person’s result, placed in the range , where is the average for the group, and is the standard deviation, should be recognized as an appropriate age or professional standard (it is shown by about two-thirds of persons in the population).
The practice shows that the test has an adequate complexity for schoolchildren from 10 years and above and can be used to assess the intelligence of schoolchildren, starting from grade 5.
It is possible to offer the following approximate recommendations on the use of the short screening test results for solving practical training problems.
When selecting students in gymnasiums, lyceums and other educational institutions with the increased requirements for students, it is advisable to focus on the indicator of the short screening test at least not less than for the contingent of students of this institution.
When organizing a differentiated education, it is desirable to allocate to individual classes (groups) of students whose the short screening test score exceeds the range for a given class or school.
In the absence of opportunities for differentiated education, it should be borne in mind that students whose the short screening test score is lower than may have difficulty in mastering the school curriculum, and teachers should pay particular attention to such students. For students whose the short screening test score is higher than , it is desirable to offer the tasks of increased complexity or to recommend admission to the gymnasium (lyceum).
Problem Statement
The application methods of various types of testing for the psychodiagnostics in the educational sphere, in particular, when analyzing the suitability of those entering the educational institution, allow for the assessment of fitness based on the results of the passed test. In this case, the availability of answers to most of the test questions allows the expert to conduct a more objective or unambiguous conclusion on the suitability of the applicant entering the educational institution.
However, in reality, there may be cases when the answers to all test questions are not received, that in turn does not allow a sufficient and adequate assessment of the knowledge of the student entering the educational institution.
At the same time, in practice there may be situations when the assessments of the test results are heavily imbalanced (for example, with an uneven distribution of the correct answers), which also complicates the psychoanalysis.
It is possible to develop various classifiers on the base of the different test surveys. In recent years, the intelligent classification algorithms, including the machine learning algorithms are widely used. The support vector machine algorithm (SVM) (Demidova & Klyueva, 2017; Demidova et al., 2016; Demodiva et al., 2017) allows to carry out the classification of incomplete and imbalanced data.
The SVM algorithm assumes the training at the base of objects with in advance predetermined classes for the purpose of the subsequent classification of new objects. A herewith, the SVM algorithm allows the possibility of classification of the original dataset if there is no information on any characteristics of the objects, with some appropriate adaptation of this dataset.
Currently there are many software tools, including tools of the SVM algorithm.
As the practice work with the use of the Python 3.5 programming language shows, its advantage is the wide range of tools for realizing the machine learning algorithms, in particular, the SVM algorithm. Also, Python 3.5 includes the tools for solving the problem of the data imbalance, in particular, the software implementation of sampling algorithms.
Research Questions
The main research questions in this work are the following:
the study of the use aspects of the psychodiagnostics data in the classifiers’ development;
the study of the problem of imbalanced data of the psychological tests;
the choice justification of the SVM algorithm and the sampling synthetic algorithm to solve the imbalance data problem;
the SVM classifier development;
the software development for the data classification with implementation of the approach to solve the imbalance data problem;
the testing on the datasets, which include the results of the psychological tests.
Purpose of the Study
The research objective is the study of applicability of the SVM classification of the imbalanced data in the analysis of the psychological tests’ results and the development of the intellectual software.
Research Methods
In the case of the binary classification problem, the objects of the original dataset are divided into two classes with labels from the set . This assumes that each object is defined by the vector of the numeric values in the -dimensional space of characteristics. Then the initial dataset can be represented by the set , in which each object ( ; is the number of objects in the initial dataset) corresponds to the number , which takes a value of "–1" or "+1" according to the object’s class [12].
From the point of view of the educational aspect in the problem of the psychodiagnostics, it is necessary to perform the SVM classification for analyzing the suitability of student for the educational institution (school, university) after passing the entrance test.
In the present work the classification was carried out for 156 objects with 4 characteristics. In this case, each object is defined by the vector of the numeric values of expert assessments of the entrance test results according to the 10-score scale.
Belonging to the class (label "–1", if the object is not suitable; label "+1" if the object is suitable) is determined in accordance with the interval in which the average scores of for all characteristics of the object are located: the object belongs to the class "–1 ", if ; the object belongs to the class"+1 ", if .
Split of the original dataset into training and test sets was produced so that the size of the test sets was equal to 20% of the original dataset size. At first, the training of the SVM classifier was provided on the training set. The labels of classes for objects of the training set were known. Then, the trained SVM classifier was used to define the class for objects of the test set. Further, the classification results of the test set were compared to a priori known data on the class of objects from test set for the purpose of the quality assessment of the trained classifier, for example, taking into account the total accuracy indicator (Demidova & Klyueva, 2017).
Training classifiers on the imbalanced datasets compromises the effectiveness of the most well-known machine learning algorithms, in particular, of the SVM algorithm. The problem of learning for the imbalanced datasets is quite common, since in the real datasets of objects the number of objects of one class in most cases is more, than the number of objects of other classes. So, in the original dataset used in the present work, the imbalance is expressed in the ratio of 70:86, where the objects of the class "+1" are referred to the minority class, the objects of class "–1" are referred to the majority class.
To solve the problem of the imbalance datasets the following sampling strategies are used (Chawla et al., 2002; He & Ma, 2013): under sampling and oversampling. In the first case, it is necessary to remove some number of objects of the majority class; in the second case, it is necessary to increase the number objects of the minority class.
One of the most famous oversampling algorithms is the SMOTE algorithm (Synthetic Minority Oversampling Technique algorithm) (Chawla et al., 2002). Nowadays, there are different modifications of this algorithm, in particular, for a more adequate account of the intrinsic properties of the objects of the minority class. One of these modifications of the SMOTE algorithm is the bSMOTE algorithm (borderline SMOTE algorithm) which implements the synthesis of new objects of the minority class for objects of the this class which are located close to the class boundaries.
In the case of the bSMOTE algorithm it is necessary to determine the optimal values of its parameters, the use of which will provide the best variant of the data rebalancing. Therefore, it is expedient to consider the different combinations of the parameters’ values of the bSMOTE algorithm with the different variants of synthesis of new objects. It is obvious that the implementation of such approach to selection of the parameters’ values of the bSMOTE algorithm has the high time expenditures.
In the present work, the bSMOTE algorithm was used for the search of the parameters’ values in the SVM-classification problem of the imbalanced datasets, which provides the reduction of time expenditures (in comparison with the similar realization on the base of the basic bSMOTE algorithm) on obtaining high values of the classification quality indicators of the SVM classifier.
The generation of new synthetic objects near the boundary objects of the minority class is carried out in the bSMOTE algorithm for the purpose of probability reduction of their wrong classification. A herewith, the boundary objects are the objects lying near the border of classes.
Thus, the bSMOTE algorithm increases only the number of the boundary objects of the minority class, while the SMOTE algorithm implies the increase in the number of all objects of the minority class. The results of experimental studies confirms the distinct advantage of the bSMOTE algorithm, because it provides the high classification accuracy of the boundary objects of the minority class.
In the present to work the search of the optimum values of two parameters of the bSMOTE algorithm is implemented: the parameter which sets the number of the closest neighbors used for creation of the synthetic objects, and the parameter which sets the number of the closest neighbors used to define whether the object of the minority class is the object on the border of classes (Demidova & Klyueva, 2017).
The software implementation of the bSMOTE algorithm for the SVM classification problem was fulfilled using the Python 3.5 environment. A herewith, the
In the
The development of the SVM classifier can be implemented with the lines of code, shown in Figure
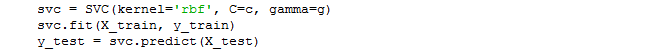
In the fragment of the program code given above the radial basis kernel function (RBF) is used for the SVM classifier development. Therefore, it is necessary to determine the parameter’s value of the radial basis kernel function. Also, it is necessary to determine the regularization parameter which allows finding the compromise between the maximization of the width of the strip separating the classes, and the minimization of the total error. The capabilities of the Python tools allow determining automatically the appropriate values for the above parameters, using the grid search tools and the cross validation tools.
To find the parameters’ values of the SVM classifier one of the bio-inspired algorithms of the stochastic optimization – the particle swarm optimization algorithm (Particle Swarm Optimization, PSO) can be used (Demidova & Klyueva, 2017, Demidova et al., 2016; Demodiva et al., 2017). The bio-inspired algorithms use the simple entities’ sets in the search space and simulate the intelligent behaviour of population in which each individual represents some alternative approximate decision. In particular, the adapting particle swarm optimization algorithm can implement the search of the parameters’ values of the bSMOTE algorithm for the rebalancing of the classes and the development of the SVM classifier, characterized by high classification quality. The software implementation of the bSMOTE algorithm can be carried out using the

The use of the Python toolkids allow accelerating the process of the program development. A herewith, the modification of the standard programs' files of the Python is possible.
Findings
The suggested searching optimization algorithm of the optimal parameters’ values of the bSMOTE algorithm can be described by the following sequence of steps (Demidova & Klyueva, 2017).
Step 1. To generate the pairs on the base of the integer parameters values from the ranges and ( ; ).
Step 2. To build for each pair SVM classifiers using the SMOTE algorithm for the imbalanced data (that is to apply the SMOTE algorithm for each pair with equal probability).
Step 3. To evaluate the classification quality of the developed SVM classifiers and save the obtained SVM classifiers. To find the best SVM classifier, if the maximum value of iteration is achieved, and finish the algorithm. Otherwise, to go to step 4.
Step 4. To estimate the average classification quality of the SVM classifiers using, for example, the F-measure indicator for each pair . To change the probabilities of application for each pair : to increase the probability for the best pair (with the maximum value of the average classification quality), and to decrease the probabilities for the other pairs . To build for each pair the SVM classifiers using the SMOTE algorithm for the imbalanced data according to the new probabilities. Go to step 3.
It is proposed to use the following ideas at the step 4 to estimate the average classification quality of the SVM classifiers for each pair :
to find the total number of the SVM classifiers for each pair , obtained to the current number of iteration of the suggested algorithm;
to find the total sum of the classification quality of the SVM classifiers for each pair , obtained to the current number of iteration of the suggested algorithm;
to find the ratio for each pair , and use it as the average classification quality of the SVM classifiers for pair .
The results of experimental studies show that the proposed algorithm which finds the parameters’ values of the bSMOTE algorithm during the SVM classifier development provides the high values of the classification quality indicators: total accuracy is equal to 99.41%, sensitivity is equal to 100.00%, specificity is equal to 98.84%.
A herewith, the time expenditures for the search of the optimum parameters’ values of the bSMOTE algorithm are equal to 426.14 seconds, and the optimum combination of the parameters’ values , found by means of the bSMOTE algorithm, is the following: (7, 26).
The experimental results obtained on the base of the model and real datasets of loan scoring, medical diagnostics, psychognosis and etc. confirm the efficiency of the proposed algorithm. Therefore, it can be recommended for the use for solving the problems of the data rebalancing in the psychodiagnostics sphere, when the SVM classification must be carried out.
Conclusion
In the present work, the experiments on the study of aspects of the SVM classifiers’ applicability to the results classification of the psychodiagnostics tests to analyze the psychological state of individuals have been conducted. The experimental results showed that the implementation of the SVM classification is useful for the solution of the psychodiagnostics problems when it is necessary to analyze the tests results of different types. In the future, it is expected to perform research based on the real test data. In particular, at the solution of the psychodiagnostics problems in the educational sphere the results of tests on the analysis of the personal uneasiness at school can be accepted as the base.
The school uneasiness (Huberty, 2012) is one of the common problems faced by the school psychologist. It is the sign of the school disadaptation, which adversely affects all spheres of life of the child: study, communication, health and overall level of psychological well-being. In psychology the following tests which consider the uneasiness level are known: "Scale of the personal uneasiness "and "Projective technique for the diagnosis of the school uneasiness", developed by Prikhozhan A.M., one of the outstanding scientists in the field of psychology, and, also, the Phillips’ questionnaire (Huberty, 2012).
The projective technique for diagnostic of the school uneasiness, developed by Prikhozhan A.M., can identify the general level of the school uneasiness of students. This technique allows obtaining information which is not dependent on the development level of the student’s reflection. In addition, the projective nature of this technique allows bypassing the "filter-importance of the school life", which often does not allow the child to reflect the negative emotions associated with the school.
The Phillips’ questionnaire (test) of the school uneasiness refers to the standardized psychodiagnostic techniques and allows to estimate not only the overall level of the school uneasiness, but the qualitative originality of the uneasiness experience which is related with the different areas of the school life. The questionnaire is not difficult to perform and processing, therefore, it can be used for the frontal psychodiagnostic examinations.
It should be noted that the results of the psychodiagnostic tests possible can be imbalanced, for example, when the answers and the corresponding expert assessments are the most relevant to the certain level of the scores scale. In this regard, it is advisable to use the proposed approach to the data rebalancing on the base of the bSMOTE algorithm.
Acknowledgments
The reported study was funded by RFBR according to the research project № 17-29-02198.
References
- Chawla, N., Bowyer, K., Hall, L., Kegelmeyer, W. (2002). SMOTE: Synthetic Minority Over-sampling Technique, Journal of Artificial Intelligence Research, 16: 341-378.
- Demidova, L., Klyueva, I. (2017). SVM Classification: Optimization with the SMOTE Algorithm for the Class Imbalance Problem, 6-th Mediterranean Conference on Embedded Computing (MECO), pp. 1-4.
- Demidova, L., Klyueva, I., Pylkin, A. (2016). The Study of Characteristics of the Hybrid Particle Swarm Algorithm in Solution of the Global Optimization Problem, 5th Mediterranean Conference on Embedded Computing (MECO), pp. 322-325.
- Demidova, L., Klyueva, I., Sokolova, Y., Stepanov, N., Tyart, N. (2017). Intellectual Approaches to Improvement Of the Classification Decisions Quality On the Base Of the SVM Classifier, Procedia Computer Science, 103:222-230.
- He, H., Ma, Y. (2013). Imbalanced Learning: Foundations, Algorithms, and Applications, Wiley-IEEE Press.
- Huberty, T. J. (2012). Anxiety and Depression in Children and Adolescents: Assessment, Intervention, and Prevention, Springer Science & Business Media.
- Rapaport, D., Schafer, R., Gill, M., Holt, R. (1968). Diagnostic psychological testing, International Universities Press.
- Rossum, G., Drake, F. L. (2011). The Python Language Reference Manual, Network Theory Ltd.
- Schafer, R. (2003). Insight and Interpretation: The Essential Tools of Psychoanalysis, Other Press.
- Thorndike, E. L. (2008). Educational Psychology, Kessinger Publishing.
- Thorndike, E. L. (2015). An Introduction to the Theory of Mental and Social Measurements – Scholar's Choice Edition, Scholar's Choice.
Copyright information

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
About this article
Publication Date
13 December 2017
Article Doi
eBook ISBN
978-1-80296-032-7
Publisher
Future Academy
Volume
33
Print ISBN (optional)
-
Edition Number
1st Edition
Pages
1-481
Subjects
Cognitive theory, educational equipment, educational technology, computer-aided learning (CAL), psycholinguistics
Cite this article as:
Demidova, L., Klyueva, I., & Pylkin, A. (2017). SVM Classification Based On The Imbalanced Datasets For Problems Of Psychodiagnostics. In S. B. Malykh, & E. V. Nikulchev (Eds.), Psychology and Education - ICPE 2017, vol 33. European Proceedings of Social and Behavioural Sciences (pp. 95-103). Future Academy. https://doi.org/10.15405/epsbs.2017.12.10

