Abstract
Rethinking the entire educational process, implicitly the mathematics education, in terms of skills training, requires identification of learning strategies to support this goal. The teacher's role requires the ability to instrument the student with such means to facilitate learning and contribute to a sustainable and effective learning.
Keywords: Learning strategymathematical competencetransfer
Introduction
Regarding the transfer, this vector dimension to learning process, the specialty literature includes phrases like: ”
In the present study, the issue of transfer is seen from the perspective of the didactics of mathematics in the context of research undertaken to identify and explain the causality of obstacles and errors in learning this aspect of knowledge. Thus, in the range of variables to be taken into account by specialists in didactics of mathematics in their efforts to find solutions to achieve an effective teaching process, transfer must also be included. The complexity of increasingly sharp expertise, the increasingly higher demands of society in general, and the dynamic of changes in the situations in which students, future adults, will need to perform based on their knowledge acquired during their training are just some of the factors that create a strong pressure on teachers and students on teaching or learning mathematics. One of the solutions recommended by research in the field, whose effectiveness is proven by practice, is the use of transfer strategies in learning. In this regard, Develay & Meirieu (1992) stated “As long as the students are not able to use the knowledge acquired in different situations, as long as they cannot pinpoint the problems that require a solution or other, the questions that demand a certain answer […] they remain dependent on the acquisition situation thus meaning that we cannot define it as a learning situation. Therefore, it is very important to practice what American researchers call
Problem Statement
From the multitude of perspectives from which the issue of transfer can be approached in learning mathematics, we will focus on the link between transfer and mathematics competence. According to Scallon (2004), “competence is the ability of an individual to mobilize in an internalized way an integrated multitude of resources in order to solve a problem-situation family”. Mobilized resources must be targeted and contextually applied, depending on the particularities of the new situation and the carrier vector of these resources is transfer. Thus, in our view, transfer is a structural component of competence.
Hereinafter we will make a brief foray into the specialty literature of transfer.
Some definitions of transfer. Notions/concepts associated with the notion of transfer extracted from researches
To create a conceptual basis of reference for the present study, we selected some definitions, which we considered to be significant to this approach: 1) “applying a known solution to a new situation, unencountered before” (Raynal & Rieunier, 2005). In the view of the same authors, attaining transfer is an
The study of transfer strategies involves two categories of interrogations:
Research on the notion of transfer highlights a series of associated notions / concepts / syntagmas:
Context of learning (physical or affective)
(Richard & Ghiglione, 1992) Specific encoder
(Tulving 1976, in. Raynal & Rieunier, 2005) Indices of information recovery from Long term memory (Raynal & Rieunier, 2005) .
Contextualizing – decontextualizing – recontextualizing: characteristics of an efficient learning situation (Raynal & Rieunier, 2005).
Ability to generalize and capacity to abstract (Raynal & Rieunier, 2005).
Acqusition and retention (Crahay & Dutrévis, 2010).
Strucutural isomorfism between two situations (one for which we have the solution, while the other one is new): when solving a problem, researches have showed that ”experts immediately search for profound structure indicators, contrary to novices (beginners) who cannot percept but surface indicators, strongly related to content” (Raynal & Rieunier, 2005 ). In opinia acelorasi autori, psychologists distinguish between structure features (logical operations necessary for solving an issue) and surface features (the form, the exterior aspect of the statement) specific for a problem. What draws the attention to a problem are mainly the surface features (with an essential role in transfer attainment), which based on an analogical way of thinking, can sometimes lead to important errors, while structural features are less accesibile, and their detection implies the students’ effort and experience. This ability to identify and distinguish not only surface features, but also structural ones develops with time, during the lessons. In this manner, the students will be able to critically analyze the issues they encounter, on one hand to sense the transfer opportunities among problems with similar structures, and on the other to prevent error emergence as a result of transfer/ interferences between surface similarities, but with different structure.The development of automatisms: “…for being able to address new and complex issues, a certain number of basic procedures need to be automatized (in arithmetic, language, writing, etc.)” (Rey et al., in Crahay & Dutrévis, 2010).
The ranking of knowledge (Crahay & Dutrévis, 2010)
Negative transfer (interference) of knowledge and compenteces which generates learning error (Crahay & Dutrévis, 2010)
And certainly not least:
The American theoretician of the instructional design, Gagné (1985), considered
transfer asthe last learning event , he was among the first who explained the importance of transfer in learning. In his opinion, one of the conditions that favours transfer is the similarity between the learning context (source situation, acc. Tardif, in Scallon, 2004) and the one in which performance is desired (target situation, Tardif, in Scallon, 2004).Astolfi has an interesting prospect of addressing transfer based on psychological theories on learning, shown in the table below:
The mathematical didactic perspectives of transfer
Research on the role of transfer in learning mathematics led to the conclusion that transfer can be learnt and it has to be done, by explaining the transfer mechanisms during learning. In this context, school should encourage transfer, without it being spontaneous, but permanently “postulated and organized, treated as a “transversal intention of schools’ mission”. The strategies for promoting transfer reside in a
In the same context, Meirieu (1987) considers that transfer supposes a metacognitive control realized by a student upon a cognitive activity and represents "an essential regulatory principle of the pedagogical activity, and that its mediation by means of teaching is decisive. The subjects do not progress unless they could change the framework, the personal experimentation of the work instruments which they possess in a newly encountered situation.” This aspect regards
The continuous nature of school learning processuality causes a double perspective on transfer: a particular sequence of its development should be considered both a result of prior learning and a subsequent learning condition. Thus, the transfer is both the condition of the learning process and a desirable result of this process. In other words, transfer is the
Research Questions
The present study is part of a broader research aiming at analyzing obstacles and errors in learning Mathematics in the secondary level. This study was prompted by the need to identify and explain the factors that generate the very large discrepancy between the results recorded by participants in national and international math competitions (performance education) and the results recorded in the national evaluations (mass education).
In this context, the question underlying the present research aims to what extent the mathematics curriculum for the secondary level has consistency in relation to the one for primary level, respectively with the high school one, in the sense of forming the adequate mathematical concepts and applicative representations for the gradient levels of complexity, and of assuring conexions between knowledge and the intra- and interdisciplinar transfer attainment.
Purpose of the Study
The research was aimed at the study of the pedagogical approach of mathematical concepts from the perspective of transversal (intra- and interdisciplinary) correlations and of their spiral evolution.
Research Methods
We used questionnaire based survey to identify the level at which vertical transfer is applied and horizontal transfer is used in learning mathematics at secondary school level.
The questionnaire has been pretested on a lot of 27 students in the 8th grade and applied in 22 classrooms, representing 19 localities (12 from rural areas and 7 from urban areas) and it has encompassed 4 counties from the South-Eastern part of Romania (adding up to 350 students). The sample, randomly established, included 8th grade students.
Findings
Variable: continuity and discontinuity of the mathematics curriculum in the secondary level
Learning based on the mathematical concepts formation, as basis for the operationalizing of knowledge and transfer attainment, implies a continuous process of their elaboration on different levels of conceptualization, according to the specific characteristics of each stage of the individual’s psychogenetic development. From this point of view, another possible source of obstacles is the discountinuities (”breaks”) which occur at those levels’ transition.
Item 1: When I learn I make connections between the new mathematical pieces of knowledge and the ones previously acquired.
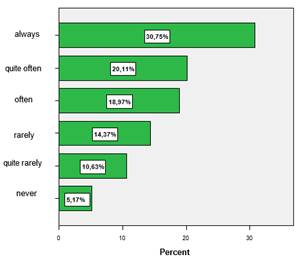
The results reveal that over 30% of the students rather do not make connections between the mathematical pieces of knowledge, which means that when these pieces of knowledge are acquired, it is more a fragmentary, thus non-functional process.
As expected, there is an important positive relation (ρ= .348 at a significance level of.01) between the attainment of these connections between the students’ Mathematics knowledge and results.
Item 2: When teaching new pieces of knowledge in Mathematics, the teacher has shown us the relation between these and the ones previously acquired.
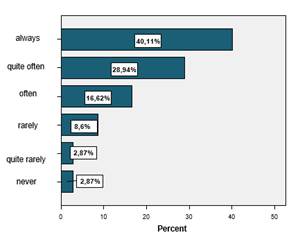
Out of the answers given by the students encompassed in the study it appears that in general (over 80% of the cases), when teaching new pieces of knowledge Math teachers highlight the elements of continuity between what the students have previously acquired and what they are in the process of acquiring. However, more than 10% claim that this happens rarely or quite rarely. Therefore, it is clear that Math teachers have included in their teaching strategies this dimension, important for the attainment of Mathematics learning.
Item3: The mathematical pieces of knowledge taught in the secondary level have been related to the ones from the primary one.
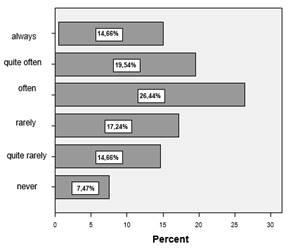
As far as the continuity between the mathematical pieces of knowledge taught in the primary level and the secondary one is concerned, to quite a great extent (almost 40% of the subjects) it has been ranked as rather unaccomplished.
Therefore, the small percentage of the cases (under 15%) in which the continuity elements between the Mathematics taught in the primary level and the one in the secondary level have been explained justifies the great part of obstacles with which students are confronted during the first part of the secondary level.
Variable: mathematics learning strategies in middle school
Item 4: When I learn, I make connections between the mathematical knowledge and the one acquired at the other subject matters.
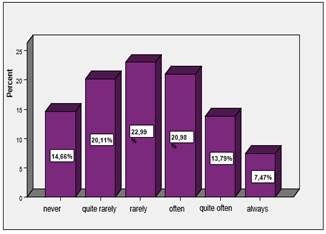
The percentual value corresponding to those who always make this type of connection (7,47%) represents half of the value of the ones that do not ever make it. Moreover, it can be observed that more than half of the students participating in the survey rather do not make connections between the knowledge acquired during the Mathemathics lessons and the one acquired at other subject matters.
Item 5: When I learn, I make connections between the mathematical knowledge and the possibilities of transferring it in everyday life.
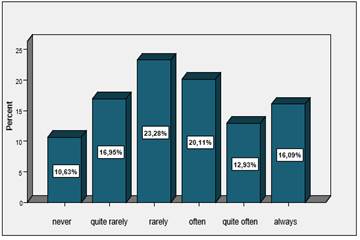
The frequency of those who always make these connections (16,09%) exceeds the one of those who never make these type of connections with almost 6%. Many (over 23%) are those who rarely link the mathematical notions to the possiblities of appling them in everyday life, and those who make these connections, to a certain extent, are less than 50%.
Conclusion
Tackling transfer through errors and obstacles in learning mathematics involves reflection on the following issues:
By the nature of the subject matter, the mathematical curriculum for the secondary level has a continuous feature, with a “spiral” evolution, in which the construction of concepts at a certain level values the previous mathematical knowledge and anticipates the future one.
For a great number of secondary level students, the attainment of connections between the previous pieces of knowledge and those in the process of being attained does not represent a component of the Mathematics learning strategy, which is in fact an
obstacle in the attainment of autenthic knowledge (based on operationalizing andtransfer ). Thus, the acquired mathematical pieces of knowledge remain fragmented and isolated, more often than not without significance (“unproductive”), energy consuming for retention and restitution in evaluation situations, far away from their integration in a field of knowledge.Math teachers should explain more the relations that can be established between the mathematical pieces of knowledge from the different levels of conceptualization. The intra– (and inter–) disciplinary transfer is a basic mental activity for the construction of the mathematical knowledge, and it has to be learned in school, by means of specific startegies, carefully projected.
Without actual diversified graphic support, the representations of students upon the studied concepts are frequently reduced to the figural models which the teacher has employed when teaching and this has negative effects on the degree of information operationalizing reducing their possibility of transfer.
In learning Mathematics, great importance is given to
making connections between pieces of knowledge (transfer), at the level of the discipline (connections among different mathematical pieces of knowledge), as well as at the interdisciplinary level (between mathematical knowledge and other fields of knowledge). Even though this aspect of learning should be more explicit during teaching, it is frequently considered the students' concern. They are not always prepared for it, thus it is attained sporadically and to a low extent in relation to its importance. As a consequence, in the absence of such transfer, mathematical knowledge remains isolated, is not integrated into the student's field of knowledge, lacks flexibility, operationality and functionality.
In conclusion, the absence of transfer is an important generating source of obstacles in learning mathematics.
References
- Astolfi, J.-P. (2004). L’erreur, un outil pour enseigner. Paris: ESF éditeur.
- Crahay, M., Dutrévis, M. (2010). Psychologie des apprentissages scolaires. Bruxelles: de Boeck.
- Develay, M., Meirieu, Ph. (1992). Émile, reviens vite…, ils sont devenus fous. Paris: ESF éditeur.
- Gagné, R.-M. (1985). The conditions of learning, 4e éd. NY: Holt, Rinehart & Winston Publihing.
- Meirieu, Ph. (1987). Apprendre... oui, mais comment. Paris: ESF éditeur.
- Raynal, F., Rieunier, A. (2005). Pedagogie: dictionnaire des concepts cles. Apprentissage, formation, psychologie cognitive, 5e Edition. Paris: ESF Editeur.
- Richard, J.-F., Ghiglione, R.(1992). Cours de Psychologie. Paris: Dunod Publihing.
- Scallon, G. (2004). L’évaluation des apprenstissages dans une approche par compétences. Bruxelles: de Boeck.
Copyright information

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
About this article
Publication Date
30 July 2017
Article Doi
eBook ISBN
978-1-80296-026-6
Publisher
Future Academy
Volume
27
Print ISBN (optional)
-
Edition Number
1st Edition
Pages
1-893
Subjects
Teacher training, teaching, teaching skills, teaching techniques,moral purpose of education, social purpose of education, counselling psychology
Cite this article as:
Căprioară, D. (2017). Transfer: Condition Or Result Of Mathematics Learning In School?. In A. Sandu, T. Ciulei, & A. Frunza (Eds.), Multidimensional Education and Professional Development: Ethical Values, vol 27. European Proceedings of Social and Behavioural Sciences (pp. 58-66). Future Academy. https://doi.org/10.15405/epsbs.2017.07.03.9

