Methods Of Demonstrating Concurrence Lines In A Tetrahedron

Abstract

This article discusses the advantages of teaching-learning Geometry with the help of the new educational technologies to motivate students and undergraduates, which may lead to building focus, interactivity and feedback during lessons. The 3rd-year students from the Department of Mathematics, “Vasile Alecsandri” University of Bacău, also attending the courses of the Pre- and In-Service Teacher Training Department, have experimented the relevance of the new technologies in teaching and learning Geometry, by applying a new approach to the design and conduct of a lesson of Geometry. The research was conducted during the 2014-2015 school year, involving two groups, each of them comprising 132 students: 66 children, from 3 classes having 22 students on the average each, experimental group – the 8th A grade from “Octavian Voicu” Middle School, Bacău, and 66 children, from 3 classes having 22 students on the average each, a control group – the 8th B grade from “Miron Costin” Middle School, Bacău and demonstrated the efficiency of teaching Geometry the concurrence of relevant lines in a tetrahedron by using computers in solving problems and promoting Geometry knowledge, building active thinking and competences, as well as skills in representing plane and space geometrical figures.

Keywords: AEL laboratoriesgraphical representationconcurrencetetrahedronexperimental research

Introduction

In order to make the economy of the European Union a most competitive one at the global level, it

is necessary to build a strong foundation for the education of future generations. In order to facilitate the

success of an economy, it is required that the physical persons owning thorough knowledge, key

competences and who are consistent with the latest technologies should firmly apply their expertise and

information to today’s society, as shown in the Lisbon Strategy.

The Lisbon Strategy is a key European orientation that plans to implement a more relevant use of

information and communication strategies in the classroom. The gaps at the educational level are very

serious. The Romanian university education should undertake a European approach in order to create new

and innovating concepts, pedagogical and didactic strategies, to improve teaching and learning(Cerghit,

2002).

The students should build key skills, including digital literacy, foreign languages and – in our

context – Mathematics, through professional training. University training should take into consideration

the students’ team-work needs within a strong European partnership and focus on improving teaching-

learning strategies.

The students’ initial training aims at a fundamental improvement of teachers at a European level.

By introducing the innovative ideas of ICT, present and future teachers should ensure a modern

professional education. This is a prerequisite for building and supporting a highly motivated society, with

a high level of awareness in Europe. (Lupu, 2013).

Building digital educational content is essential for the use of modern information and

communication technologies in mathematical education (both in schools and universities). We shall

present and evaluate the experience in using modern educational software in and outside the classroom.

The teachers from Romanian schools are interested in using AEL laboratories and ICT during

lessons, as well as dynamic mathematical software for teaching and learning. Also, there is required the

use of the interactive board in everyday lessons, hence every school should have an interactive board. The

relevance of the role of teachers as partners of students was highlighted by the use of laboratory-

digitalised environments in mathematical training.

A concern of university teachers is to organize courses or workshops on the use of computers in

teaching Mathematics, with the aim of training middle and high-school teachers in this respect.

Mathematical software represents a highly supportive component for encouraging individual learning and

solving Geometrical problems, by providing students and undergraduates with tools that may be

individually used inside, as well as outside the classroom, in the initial training of teachers.

During the Teaching Practice, the students and pupils from the research group used AEL programs

to graphically represent geometrical figures, mainly tetrahedrons, highlighting relevant lines and

concurrence properties.

The experimental research consisted in evaluating some initial, formative and final tests that

highlighted the importance of using computers, as well as acquiring the relevant lines in a tetrahedron,

with their concurrence properties.

Theoretical Aspects. The Concurrence of Relevant Lines in a Tetrahedron

We shall analyse some concurrence problems of the following relevant lines in a tetrahedron: the

medians (the segment connecting a point with the centre of gravity of the opposite side), the bimedians

(the segment uniting the middle points of two opposite edges), the perpendiculars to the sides of the

tetrahedron on their centres. There rose the following problem-situations: Are the heights in a tetrahedron

concurrent? Is there a condition if and only if, that ensures that the heights in a tetrahedron are

concurrent? (Lupu, & Săvulescu, 1999, p.84) Problem 1. Let M be the middle of the edge CD of a tetrahedron ABCD, and I∈BM and J∈AM

the points of the centres of gravity of the sides BCD and ACD. Prove that the medians AI and BJ are

concurrent. (Lupu, & Săvulescu, 2000, p. 127)

Demonstration: Because I and J represent the centre’s of gravity of sides BCD and ACD, they will

!!

be located on medians BM and AM at ! from CD and ! from vertex B and A. In triangle ABM, ∥ 𝐴𝐵

!"!"!"!"!"!

and let there be 𝐴𝐼 ∩ 𝐵𝐽 = 𝐺 , then !"=!"=!"=!"=!"=! . The medians of the tetrahedron,

being coplanar two by two, are also concurrent two by two, therefore they have a common G point that

divides each median according to the relation1/3 and is called the centre of gravity of the tetrahedron.

Regarding the concurrence of medians, there is demonstrated that: In a tetrahedron ABCD, the medians MP, NQ are RS are concurrent. (M∈BC, MB≡MC ; N∈CD , NC≡ND ; P∈AD , PA≡PD ; Q∈AB , QA≡QB

; R∈AC, RA≡RC ; S∈BD , SA≡SO).

For demonstration, observe that the quadrilateral MNPQ is a parallelogram, and QN and MP are

concurrent, being diagonals in this parallelogram and cut into half. By analogy, RS cuts the middle of QN

and MP. We may further demonstrate that the concurrence point of the medians is also the centre of

gravity G, because the median MP, for example, is the median of the median plane (MAD) and of the

median plane (NBD), and since the gravity centre belongs to each of the median planes of the

tetrahedron, it results that G also belongs to each median. (Peligrad, Ţurcanu, & Popa , 2015).

Regarding the concurrence of the perpendiculars on the centres of the circles circumscribed to the

lateral sides, we will first solve the fact that the bisecting planes of the sides of a triangle have a common

line. Building the bisecting planes  and  of sides AB and BC from ABC we will have ∩ = PO and 𝑃𝐴 ≡ 𝑃𝐵 ≡ 𝑃𝐶. Line PO of the intersection of the bisecting planes of triangle ABC is the median in space of this triangle and every point on it is equally distanced from the triangle tips.

Then, we demonstrate that the six bisecting planes of the sides of a tetrahedron are concurrent in a point that is equally distanced from the vertices of the tetrahedron. If m1 is the median in space of the plane of triangle ABC and  the bisecting plane of the edge AD where O = m1∩, we have: 𝑂𝐴 ≡ 𝑂𝐵 ≡

𝑂𝐶 ≡ 𝑂𝐷 = 𝑅 which shows that O also belongs to the other bisecting planes.

The sphere with the centre O and radius R is called the sphere circumscribed to the tetrahedron.

Are the heights concurrent? The answer is no. We may illustrate it with an example: in the tetrahedron

DABC with the basis an equilateral  ABC and DA ⊥ (ABC), the heights BM, CN and DA are not

concurrent. Regarding the fact that the heights of a tetrahedron should be concurrent, we shall firstly

define the orthocentric or orthogonal tetrahedron (a term coined by Steiner in 1927), namely, a

tetrahedron is orthocentric if its opposing edges are perpendicular.

Lemma: If in the tetrahedron ABCD two pairs of opposing edges are perpendicular, then the other

two edges are also perpendicular.

Demonstration: Let there be AB ⊥ CD and BC ⊥ AD. Draw AE ⊥ DC and AF ⊥ BC. It results CD ⊥ (ABE) and BC ⊥ (ADF). If AAʹ = (ABE)∩ (ADF) then AAʹ⊥ (BCD). But CAʹ⊥BD and therefore

BD⊥(ACAʹ), it results BD ⊥ AC. Then, demonstrate the theorems.

Theorem 1: The heights of a tetrahedron are concurrent if and only if the tetrahedron is orthocentric.

Demonstration: We demonstrate that the heights from A and D are concurrent when AD⊥BC. Let

Aʹ and Dʹ be the orthogonal projections of points A and D on planes (DBC) and (ABC) and AAʹ and DDʹ

concurrent, AAʹ⊥(DBC)⇒AAʹ⊥BC and DDʹ⊥(ABC)⇒DDʹ⊥BC. Therefore, BC being perpendicular to

plane (AAʹ,DDʹ), it is therefore also perpendicular to AD. Reciprocally, if AD⊥BC, let F be the foot of

the perpendicular from A to BC. From BC⊥AD and BC⊥AF it results that BC⊥(AFD)⇒BC⊥AAʹ .

Analogously, BC⊥DDʹ. Since AAʹ⊂(AFD) and DDʹ⊂(AFD) it results that AAʹ and DDʹ are heights in

triangle (AFD), therefore are concurrent. Hence, it results that if the heights AAʹ and DDʹ are concurrent,

then the other two heights BBʹ and CCʹ are also concurrent. Indeed, AAʹ∩DDʹ∅⇒ AD ⊥ BC therefore

BBʹ∩ CCʹ∅.(Lupu, 2014, p. 135).

We may demonstrate that if heights AAʹ and BBʹ are concurrent in H, then the common

perpendicular of edges AD and BC contains the point H, because if the plane (AAʹ,DDʹ) cuts BC in F, it

results that FH is the third height, therefore FH⊥AD; since BC⊥(AFD) ⇒ FH⊥BC. By analogy, we may

demonstrate that if the heights AAʹ and DDʹ are cut in point H and BBʹ and CCʹ in Hʹ≠ H then HHʹ is the

common perpendicular of the opposing edges AD and BC.

From the three conditions of perpendicularity of the orthocentric tetrahedron, it results the

concurrence of heights. Another particularly interesting theorem for analysis is: Theorem 2: A tetrahedron is orthocentric if and only if: 𝐴𝐵!+ 𝐶𝐷!= 𝐴𝐶!+ 𝐵𝐷!= 𝐴𝐷!+ 𝐵𝐶!.

Demonstration: We demonstrate, first of all, that the heights from A and D of tetrahedron ABCD are secant if and only if𝐴𝐵!+ 𝐶𝐷!= 𝐴𝐶!+ 𝐵𝐷!. Let there be F and F1 the orthogonal projections of

points A and D to BC. There occur the relations: 𝐴𝐵!− 𝐴𝐶!= (𝐴𝐹!+ 𝐵𝐹!) − (𝐴𝐹!+ 𝐹𝐶!) =

𝐵𝐹!− 𝐹𝐶!= 𝐵𝐹 + 𝐹𝐶 ∙ 𝐵𝐹 − 𝐹𝐶 = 𝐵𝐶 𝐵𝐹 − 𝐹𝐶 1 ; 𝐵𝐷!− 𝐶𝐷!= (𝐷𝐹!! + 𝐵𝐹!!) −

(𝐷𝐹!+ 𝐹!𝐶!) = 𝐵𝐹!! − 𝐶𝐹!! = 𝐵𝐹! + 𝐶𝐹! ∙ 𝐵𝐹! − 𝐶𝐹! = 𝐵𝐶 𝐵𝐹! − 𝐶𝐹! 2 .

It can be observed that AAʹ and DDʹ are secant if and only if F coincides with 𝐹!. From the

previous equalities with 𝐹 = 𝐹! ⇒𝐴𝐵!− 𝐴𝐶!= 𝐵𝐷!− 𝐶𝐷!⇒𝐴𝐵!+ 𝐶𝐷!= 𝐵𝐷!+ 𝐴𝐶!.

Reciprocally 𝐴𝐵!+ 𝐶𝐷!= 𝐵𝐷!+ 𝐴𝐶!⇒ 𝐵𝐶 𝐵𝐹 − 𝐹𝐶 = 𝐵𝐶(𝐵𝐹! − 𝐹!) therefore 𝐵𝐹 − 𝐹𝐶 =

𝐵𝐹 + 𝐹𝐹! −

− 𝐹𝐹! + 𝐹𝐶 = 2𝐹𝐹! = 0 therefore F and 𝐹! coincide. Demonstrating analogously and taking

into consideration the concurrence of all the other heights, it results: 𝐴𝐵!+ 𝐶𝐷!= 𝐴𝐶!+ 𝐵𝐷!= 𝐴𝐷!+

𝐵𝐶!. We can also easily deduce the fact that the tetrahedron ABCD is orthocentric if and only if its three

bimedians are congruent(Lupu, 2015, p. 850).

Research Description

Research Results

This study is a continuation of our previous articles (Lupu, 2014 & Lupu, 2015) where we have

demonstrated that informational technologies hold a privileged position within the set of the factors

responsible for the students’ school success and how using computers and active, cooperation methods during

Geometry lessons has a positive effect upon students, supporting the building of digital, communication and

team-work skills.

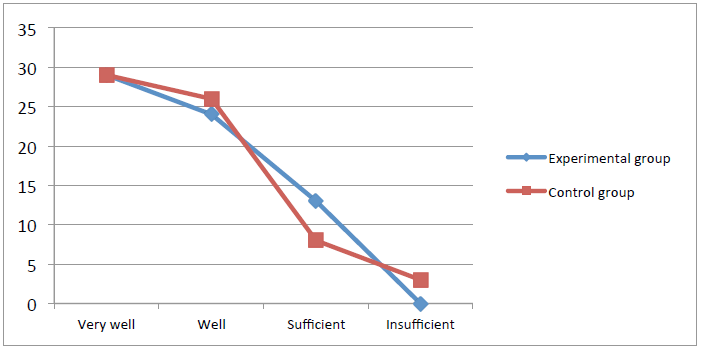
The analysis of the analytical and synthetic tables, the histogram, the frequency polygon and the

circular diagram generated the following conclusions regarding the initial evaluation: the experimental

group has achieved the following results: of the 66 evaluated children, 29 obtained the mark of very well,

representing 44% of them, 24 children obtained the mark of well, meaning 36%, and 13 children obtained

the mark sufficient, representing 20% of the participants; the control group achieved the following

results: of the 66 evaluated children, 29 obtained the mark very well, representing 44% of them, 26

children obtained the mark well, namely 40%, and 8 children obtained the mark sufficient, representing

12% of the participants, whereas 3 children – 4% got insufficient.

The application of the initial test enabled the identification of the students’ gaps and the extent of

these gaps, the prolonged emphasis on the concurrence of relevant lines until all the students have

reached a corresponding training level. In Table 1 and frequency polygon 1, shows the comparative

analysis of the initial evaluation for the two groups.

At the current, formative stage, in the experimental class the focus was particularly on issues

related to the use of computers in the graphical representation of planes and geometrical figures, on

solving and demonstrating problems.

Thus, there were regularly applied, during lessons of Mathematics, formative evaluation tests.

Thus, the students solved tests based on the hypothesis that the permanentization of immediate control, as

an extrinsic motivational situation, would build the motivation needed in building digital skills,

imagination and creativity by solving problems through the use of the computer in graphical

representation.

The formative evaluation tests applied in lessons of Geometry enabled the immediate

identification of the students’ learning difficulties. In order to eliminate mistakes, the activity was

differentiated. Following the analysis of tests, there were presented the operational objectives that were

not achieved by students, so that they may be aimed at in the proposed recovery activities.

See Full Size >

See Full Size >

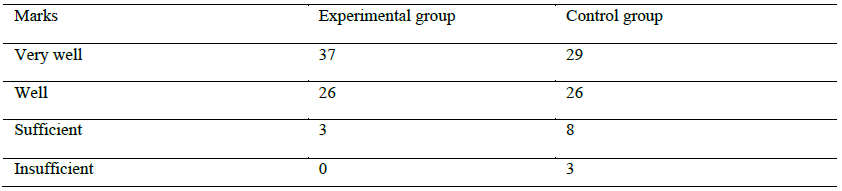
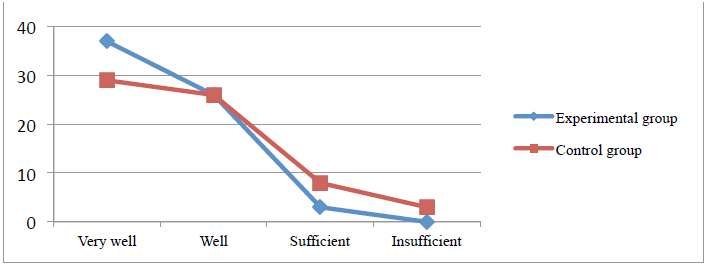
The analysis of the synthetic table no. 2, the histogram and the frequency polygon reveals the fact

that, in the final evaluation: - for the experimental group, the results were the following: of the 66

evaluated children, 37 obtained the mark very well, representing 56% of them, an increase by 12% , 26

children obtained the mark well, their percentage also being 40 %, and 3 child got the mark S (sufficient),

representing 4% of the participants; - for the control group, the results were the following: of the 66

evaluated children, 29 obtained the mark very well, representing 44% of them, 26 children obtained the

mark well, their percentage also being 40%, 8 children got the mark sufficient, representing 12 % of the

participants, and 3 child insufficient, representing 4 % .

Calculating the average between the two tests (initial and final), and drawing a comparison

between the two groups, there may be observed an increase in the school performance at the experimental

group, compared with the control group.

The comparative analysis of the histogram and frequency polygon no. 2 reveals the progress

recorded by the experimental group at the end of the experiment. Calculating the average between the

initial and final evaluation, there were obtained the following results.

See Full Size >

See Full Size >

Conclusions

At the theoretical level, there were created the premises for conceptualizing the teaching strategies

for solving problems of Geometry in the concurrence of relevant lines in a tetrahedron. The analysis of

the experimental test from the two classes supports the formulation the following conclusions: - the

informational technologies hold a privileged position within the set of the factors responsible for the

students’ school success; - using computers and active, cooperation methods during Geometry lessons has

a positive effect upon students, supporting the building of digital, communication and team-work skills; -

the efficient use of AEL laboratories and the use of software characteristic of geometrical representation,

as well as active-participative methods constitutes a challenge, both for students and the teacher.

Following the application of the ameliorative experiment by using the method of the tests, as well as of

active, cooperation methods in teaching, it was found that their use with a specific purpose, at the right

moment, may generate satisfying results, such as: - the students overcame their communication

blockages; - they built skills in solving Geometry problems; - they manifested proper behaviour towards

their colleagues and group; - there was better cooperation among children, these became more tolerant; -

there was a combination of types of work (frontal, group, individual), which created great possibilities for

the multiple and diverse activation of students; - the students learnt that in order to achieve a group task,

they need one another.

The results obtained by the students validated the research hypothesis. The use of modern

technologies in the activity of solving Geometry problems contributes to optimizing learning and

rendering it efficient, stimulating the students’ intellectual and creative potential, obtaining performances

according to age and individual particularities.

In conclusion, we may say that in order to achieve quality education and obtain the best results, we

should apply the project “InnoMathEd – Innovations in Mathematics” and combine traditional and

modern methods in the teaching-learning-evaluation of Mathematics.

References

1. Cerghit, I. (2002). Alternative and complementary training systems. Structures, styles and strategies,
2. Aramis Publishing, Bucharest.
3. Cristea, S. (2003). Science education. General theory of education. Letter Publishing Group / Point
4. International, Chisinau, Bucharest.
5. Dewey, J. (1992). Foundations for a science of education, Didactic and Pedagogical RA, Bucharest. Landsheere, V. & G. (1979). Defining learning objectives, (trans.), Didactic and Pedagogic Publishing House, Bucharest.
6. Lupu, C. & Savulescu, D. (1999). Teaching Mathematics. Manual and college teaching class XI, Publishing House, Parallel 45, Pitesti.
7. Lupu, C. & Savulescu, D. (2000). Teaching Geometry, Publishing House Parallel 45, Pitesti.
8. Lupu, C. (2013) Demonstration by Reducing to Absurd , Procedia Social and Behavioral Sciences, Vol. 76, pp. 465-469. http://www.sciencedirect.com/science/article/pii/S1877042813006903.
9. Lupu, C. (2014) The Model Object-product-cognitive Operation Through Mathematical Education, Procedia - Social and Behavioral Sciences, Vol.163, pp. 132 – 141, http://www.sciencedirect.com/science/article/pii/S187704281406399X Lupu, C. (2015), Methods of Demonstrating the Collinearity of Points in Space, Procedia - Social and Behavioral Sciences, Vol. 180, pp. 847-853, DOI: 10.1016/j.sbspro.2015.02.223.
10. Peligrad, S., Ţurcanu, A., & Popa, C. S., (2015), Final evaluation standard tests. Class VII. Mathematics, Publishing House Parallel 45, Pitesti.