Mathematical Modelling in the Teaching-Learning Process in Romania

Abstract

For an alignment with the international teaching-learning methods, for achieving new competences and for obtaining better results in the PISA tests, we debate the Mathematical modelling which represents the connection between the processes in the real world and Mathematics. Modelling, as a teaching-learning process of Mathematics, has a highly developed theoretical context, researched and sustained even through the curriculum in different countries. Modelling helps the concret-intuitive thinking, and also helps someone keep in mind the information for a long-term. The present study answers to some basic questions: How much and how is the Mathematical modelling implemented in Romania? Which would be the plus value of the implementation in the teaching-learning process in the primary school? In the second part of this paper there are developed some examples of problems which could be the basis of the application of mathematical modelling in the primary school. We consider that these changes are quite necessary for the Romanian schooling system because they have been tested, successfully implemented and recommended to the teachers by the ministries which deal with education in many different countries-after a careful research, international projects.Even if this method is not developed in Romania, it could be successfully adopted if their results upon the students prove to be useful for their training and for a fast integration in the European labour market and so on. In this way, the alignment with efficient international standards could be done in a rhythm which is favourable for the human resource in our country.

Keywords: Mathematical modellingteaching-learning process

Introduction

This paper represents a basic research whose main purpose is to increase the understanding of

mathematical modelling phenomenon and of the advantages of its application in the Mathematics

teaching-learning process and so on. Its purpose is not, in fact, the research through a group of

participants, but helping the primary and secondary school teachers to become aware of what

mathematical modelling means. Understanding the practical side of mathematical modelling (the

possibility of applying it in the daily activities) is another important goal. The practical example of other

countries and the results in the international assessments are the strongest arguments in this way.

Theoretical Context

The varied research, which have the mathematical modelling as a base, determined the inclusion of

this kind of reality approach in the educational curriculum. Many advantages were experimented by

countries which have spectacular evolutions in the training focused on the fast integration in daily

activities and which do not give the same high importance to theoretical training in schools. These

advantages are presented in the international research of different countries such as Singapore: ”in

Singapore, mathematical modeling was first incorpored in the mathematics curriculum framework in

2003”(Lee &Ng, 2015, p. 3), Germany: ”in Germany, for instance, mathematical modelling is one of six

compulsory competencies in the new national Education Standards for mathematics” (Blum, 2011, p. 19).

In the order expressed by the Italian Minister of Education in 2007, we may find: ”A characteristic of

practical mathematics is the solution of problems, which must be viewed as authentic, meaningful

questions, often linked to daily life, and not mere repetitive exercises or questions to which the children

answer simply by remembering a procedure or a rule” (Bonotto, 2010, p. 18). Iranian documents:

”opportunities to explore real-life application make mathematics more meagniful for students and aid in

the development of important other skills” (Bahmaei, 2011, p. 3), Erik De Corte, LievenVerschaffel

(Belgium) and Brian Greer (USA) said that ” a major argument for including verbal problems in the

school curriculum has always been their potential role for the development in students of skills in

knowing when and how to use their mathematical knowledge for approaching and solving problems in

practical situations” (De Corte, E. Verschaffel, L., &Greer, 2000, p. 3), ”during the last couple of decades

the introduction of mathematical modelling and applications is probably - together with the introduction

of information technology - the most prominent common features in mathematics curricula reforms

around the world” (Blomhoj&Carreira, 2009, p. 1), ”The mathematical modeling presents itself as a

pedagogical strategy that complements this association between real application and the utilization of

computational resources, as it provides for the construction of favorable environments for the students to

choose their problems of interest, gather their own data, and participate on the investigations, analysis,

discussions and reflections” (Ferreira &Jacobini, 2009, p. 26). A good idea is expressed by Neacsu in

Chapter VIMethods and techniques of arguing, counter-arguing and persuading : “problem-solution

model is considered more effective than option solution-problem, appreciating that it induces a stronger

motivation” (Neacșu, 2015, p. 292).

The mathematical modelling definitions lead to the same answer which is the following:

”mathematical modelling is a process of representing real world problems in mathematical terms in an

attempt to find solutions to the problems. A mathematical model can be considered as a simplifications or

abstraction of a complex (real) world problem or situation in a mathematical form” (Cheng, 2001, p. 64).

Mathematical Modelling in the Primary School

Even if the mathematical modelling seems to be closer to a theoretical concept, it has varied

applications, starting from the primary school. In the higher classes, the mathematical modelling can be

applied and developed even on problems which have a greater applicability, in many other domains.

Pupils should be connected to reality when they solve any kind of problem, to think about the

match between the data of the problem and the reality, if they can be changed in agreement with the

present (and issue that teachers should accept). They should solve more and more Mathematics problems

which the community might face and they also should answer with responsibility when giving the

solution. Different studies proved that when pupils in a standard / traditional class had to face

Mathematics problems, they answered correctly in a lower degree than in the case when the same

problem was integrated in a realistic context. DeFranco and Curcio experimental study is representative.

Throughout this study, it is presented the implication in solving a Mathematics problem correctly: „328

older people go on a trip. 40 people can sit down in a bus. How many buses are needed, so that all people

may go on trip?” (DeFranco, Curcio, 1997, p. 60). It is presented in two ways: Firstly, as a traditional test

of Mathematics, and secondly, the problem is integrated in a more realistic background: the pupils answer

to the phone by means of a teletrainer in order to order buses for the transport to a party. The reserchers

concluded that 2 of 20 (in the case of classic problems lesson) answered as in the real conditions of the

problem. In the opposite case, 16 of 20 answered as expected, they being involved in situations which

simulated the reality, the problems being apparently real.

In „Mathematical Modelling Handbook” there are presented real Mathematics problems which

make the pupils give correct answers. Look at the following example: „your neighbour is ornithologist

and this weekend, he leaves for research. He asked you to feed his birds. The food vase is cylindrical, as a

tree, having some holes so that the birds may feed. He asked you not to leave the vase empty because the

birds would leave in the woods for food, but also you should not leave the vase full because refilling it

too often scares the birds”(Gould, Murray &Sanfratello, 2012, p. 21).

This way of teaching Mathematics- mathematical modelling - means that teachers should add

modelling activities in the training process in order to stimulate thinking, encourage pupils to discover

new things by themselves, in order to generate more questions/ answers which are quite necessary in the

case of a real problem. As BonottoCinziasuggests the teachers all around the world: each problem should

not have only one solution anymore, and just a correct solving variant. The numbers given in the problem

could be adapted to the children’s reality, they could be insufficient or to many for a certain context,

which could be developed around a certain problem; the solving modality should be a open way which

follows the stepts of a solving framework only in case that the pupils cannot find the solution by

themselves (Bonotto, 2010, p.19).

Recommendations for Application of Mathematical Modeling in Romania

Nowadays, teachers training should contain mathematical modelling of real phenomena. The

programmes do not have this kind of initiatives, Mathematics teachers follow the traditional patterns,

which help them solve more problems and exercises in a smaller amount of time. They allow, in a lower

degree (if the classbooks and workbooks contain problems which are adapted to children’s reality), the

discussions/ modelling possible solutions for a real problem. The teachers’ role in the teaching-learning

process with the support of mathematical modelling is crucial, because s/he can bring the pupil closer to

the actual reality, motivate him so that learning is achieved beyond the classroom. Moreover, she can

motivate te pupil to apply Mathematics in the real life.

There are recommendations throughout the teachers’ role importance for the community is

demonstated (a teacher who adopts the mathematical modelling). She may simulate, by means of

mathematical modelling and with the pupils’ help, how much water, food or how many places for

accomodation are needed on an island during the touristic season. One should start from the real figures

and, then, generate answers regarding different topics. Another option is that one should start from a

major question and then generate smaller problems which can be solved. An incipient form would be the

methods which are also learnt in Romania: the analytical method and the synthetic method. The teacher’s

role is quite important because these activities could be done in groups, so that the amount of work can be

divided and properly capitalized (searching for real data on the Internet, processing, making predictions

according to them etc.).

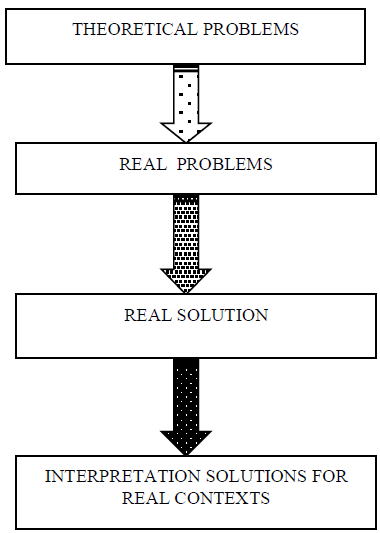
If we proposed an algorithm designed in order to facilitate the practical application of

Mathematical modelling in Romania, it would look like:

1. children's training in order to give "true" answers;

2. transfer the theoretical problems in real contexts;

3. the provided solutions may solve the "real" problems which are presented;

4. the interpretation of the results for more real situations.

See Full Size >

Conclusions

This paper tries to bring a contribution to the rethinking of new strategies on how Mathematics

should be approach in the teaching-learning process. These strategies should lead to a correct application

of the Mathematics concepts in real activities/processes.

From an educational point of view, the mathematical modelling should help the pupils to

undertstand better and deeper the real world, to sustain the mathematics learning (by means of

motivation, helping the pupils to keep in their minds the information), to contribute to the development of

different mathematical skills and competences; to contribute to a proper image of mathematics (Blum,

2011, p. 19). Leaving the classic problems conventionalism in order to use problems which can be

applied in the daily life, involving the computer in the teaching-learning activities, and also in the

evaluation process (simulations, examples, videos containg daily situations) and thinking of new

strategies (adapted to the nowadays chlidren’s thinking style) may lead to a better understanding of the

information, facilitate the assimilation of theoretical information and the applicability in the real world.

Even if the amount of time seems to be limited for such activities in the Romanian education

system, with a proper strategy, adapted to the class level, with a real motivation in the case of the teacher

and a real awareness of the positive effect for children, one can reach performance in motivation, score

and applicability, perfomance which is obviously higher than in the case of traditional, classic, stereotype

and theoretical tests.

References

1. Bahmaei, F. (2011). Mathematical modelling in primary school, advantages and challenges, Journal
2. of Mathematical Modelling and Application, Vol. 1, No. 9, Iran, pp.3-13.
3. Blomhøj, M., &Carreira,S.(2009). Mathematical applications and modelling in the teaching and learning of mathematics, Proceedings from Topic Study Group 21 at the 11th International Congress on Mathematical ducation in Monterrey, Mexico, Nr.461/2009.
4. Blum, W. (2011). Can Mathematical Modelling Be Taught and Learnt? Some Answers from Empirrical research. In Kaiser, G., Blum, W., Ferri, R.B., & Stillman, G. (Eds) Trends in teaching and learning mathematical modelling, International Perspectives on the teaching and learning of mathematical modelling, ICTMA14(pp. 15-27)Springer Science and Business Media B.V.
5. Bonotto, C.(2010). Engaging Students in Mathematical Modelling and Problem Posing Activities, Journal of Mathematical Modelling and Application 2010, Vol. 1, No. 3, pp. 18-32.
6. Cheng, A. K (2001). Teaching mathematical modelling in Singapore schools, The Mathematics Educator, Vol. 6, No.1, pp.63-75, Association of Mathematics Educators .
7. De Corte, E. Verschaffel, L., &Greer, B. (2000). Connecting Mathematics Problem Solving To The Real World, Belgium.
8. De Franco, T.C., &Curcio, F.R. (1997). A division problem with remainder embedded across two contexts: children’s solutions in restrictive versus real world settings, Focus on Learning Problems in Mathematics, 19 (2) (1997), pp. 58–72.
9. Ferreira, D. H. L., &Jacobini, O. R. (2009). Mathematical modelling: From classroom to the real world. In M. Blomhøj& S. Carreira (Eds.), Mathematical applications and modelling in the teaching and learning of mathematics: Proceedings from TSG21 at the ICME11 (pp. 35–46). IMFUFA-text no. 461, Department of Science, Systems and Models, Roskilde University.
10. Gould, H., Murray D.R., &Sanfratello A.(2012). Mathematical Modeling Handbook, Columbia University.
11. Kaiser, G., Blum, W., Ferri, R.B., &Stillman, G. (2011). Trends in teaching and learning mathematical modelling, International Perspectives on the teaching and learning of mathematical modelling, Springer Science and Business Media B.V.
12. Lee, N.H,& Ng, K.E.D. (2015). Mathematical Modelling: From Theory to practice, Series on Mathematical Education, Vol.8, World Scientific Publishing Co. Pte. Ltd., Singapore.
13. Neacsu, I. (2015).Methods and Techniques for Effective Learning. Fundamentals and Successful Practices, Iași: Polirom.