An Example of the Training a Methodological  Competences in Mathematical Analysis

Vălcan, Teodor-Dumitru

doi:https://doi.org/10.15405/epsbs.2016.12.78

An Example of the Training a Methodological Competences in Mathematical Analysis

Abstract

In this paper we try to present some simple methods of training and development of professional competences, more specifically methodological, for obtaining the identities mathematical (combinatorial) and their use. Thus, starting from a simple integral, we obtain multiple identities mathematical (combinatorial), that, then we will use in calculating limits of sequences and some primitives, respectively definite integrals. The attentive reader and interested in these issues will notice that the results of this work complete and definitive resolves many problems of Mathematics. Therefore we consider that the work will be of real help to students who are preparing for competitions and Olympiads, students in deepening their knowledge and passing exams and teachers in their professional training. Of course not here we present all types of exercises that can solve with the formulas proven in the paper. There are other types of exercises than those presented herein and we will present in a forthcoming paper.

Keywords: Professional competences; identities mathematical; limits of sequences; primitives definite integrals

Introduction

As we have presented in Abstract, in this paper we intend to present some simple ways of training and development of professional competences, more specifically methodological, for obtaining the identities mathematical (combinatorial) and their use. Thus, starting from a simple integral, we obtain multiple identities mathematical (combinatorial), that, then we will use in calculating some limits of sequences and some primitives, respectively definite integrals. The attentive reader interested in these issues and will notice that the results of this work complete and definitive resolves many problems of Mathematics, using, exclusively, the results can be presented in class, so in preuniversity education, without using superior results in Mathematics.

Main results

The main results of the paper we will obtain starting from a definite integral. So, let be p, q N and consider the definite integral – see Mocica (1988) or http://mathworld.wolfram.com/zetafunction:

I(p.q)=

. (1)

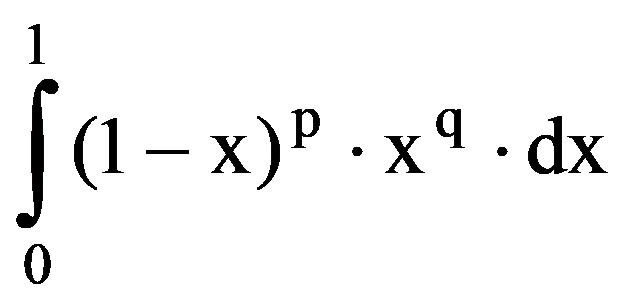
Using the binomial theorem (of Newton), we obtain that:

I(p.q)=

=

=

C

. (2)

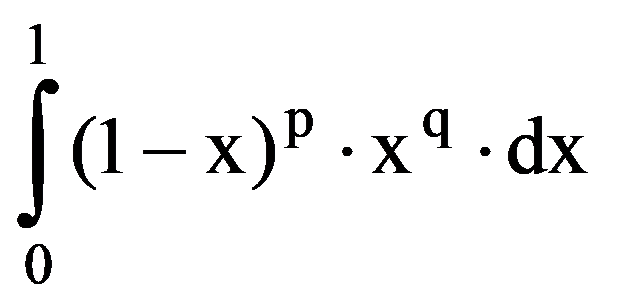
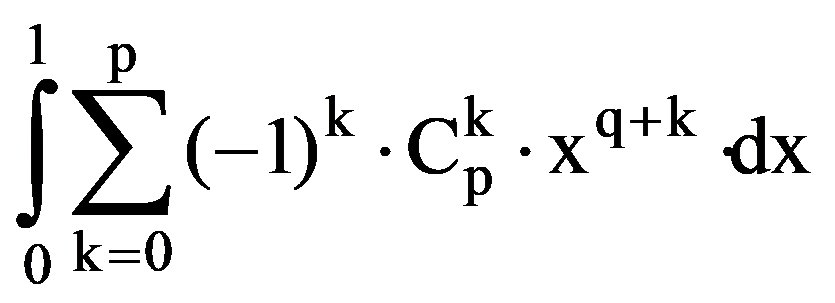
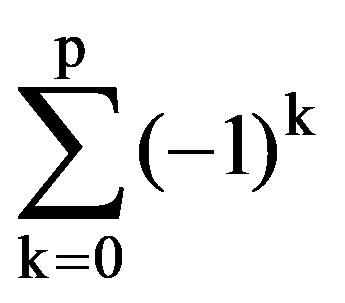
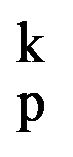
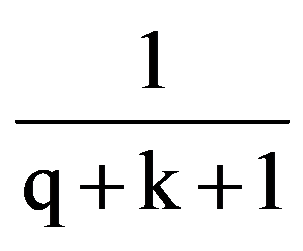
But, by making change of variable 1-x=y, obtain that:

I(p.q)=-

=

=I(q,p). (3)

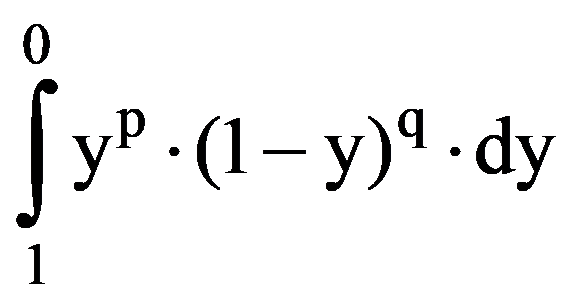
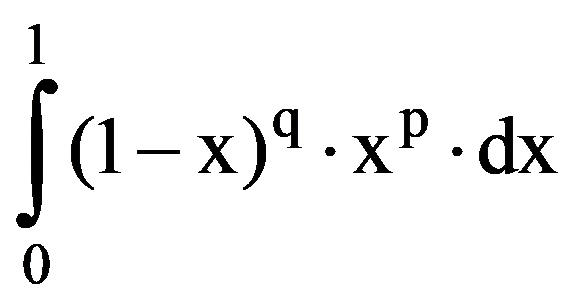
By proceeding as above – in (2), obtain that:

I(q,p)=

C

. (4)

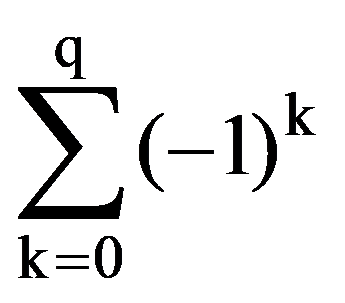
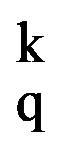
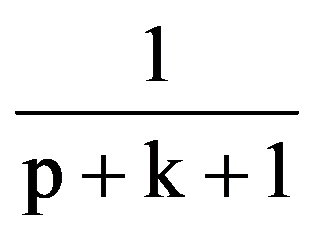
From the equalities (2), (3) and (4) it follows that:

C

=

C

; (5)

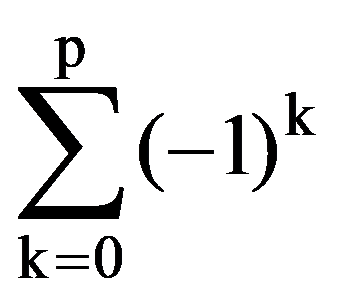
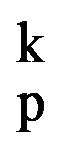
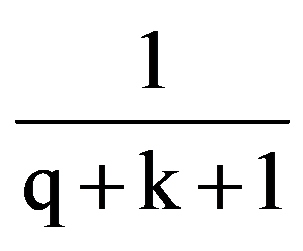
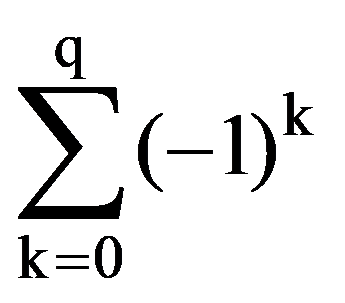
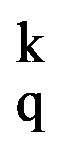
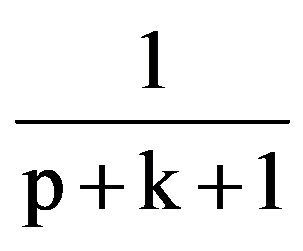
i.e.:

-

+

-

+(-1)^p

=

-

+

-

+(-1)^q

. (5)

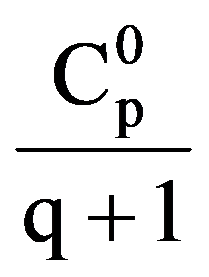
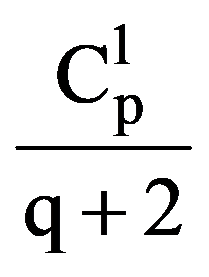
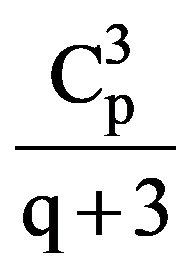
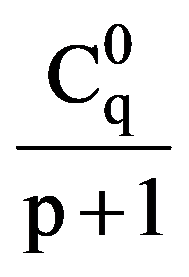
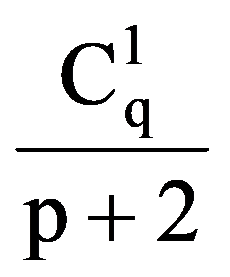
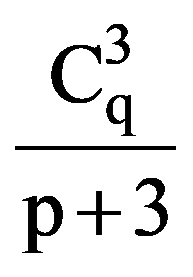
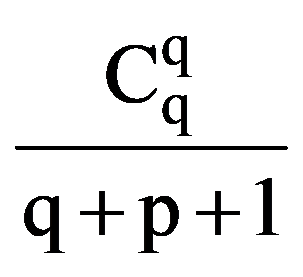
On the other hand, integrating by parts, obtain that:

I(p.q)=

+

=

I(p-1,q+1). (6)

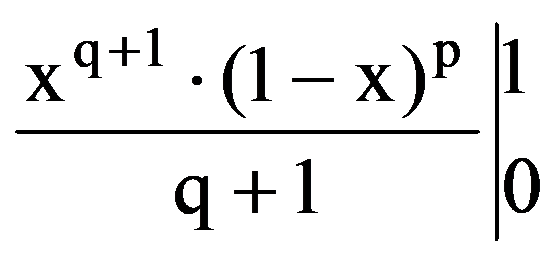
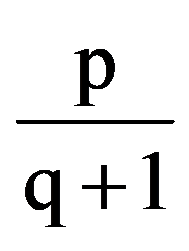
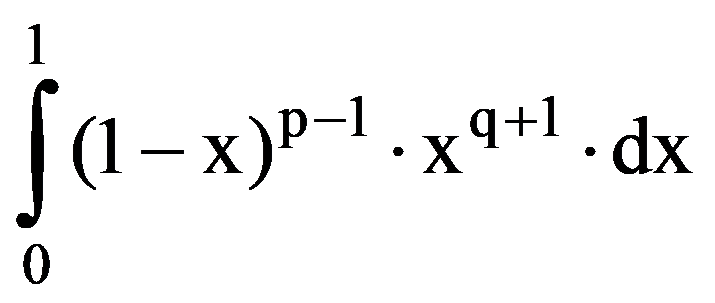
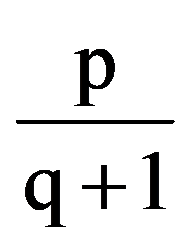
From the equalities (6) it follows that:

I(p,q)=

I(p-1,q+1)=

=

I(0,q+p)

=

=

. (7)

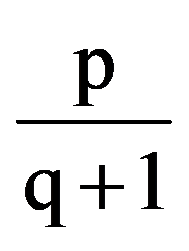
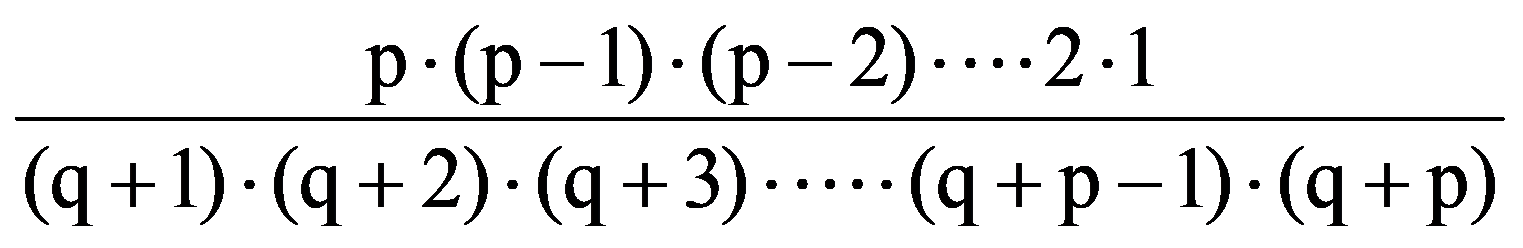
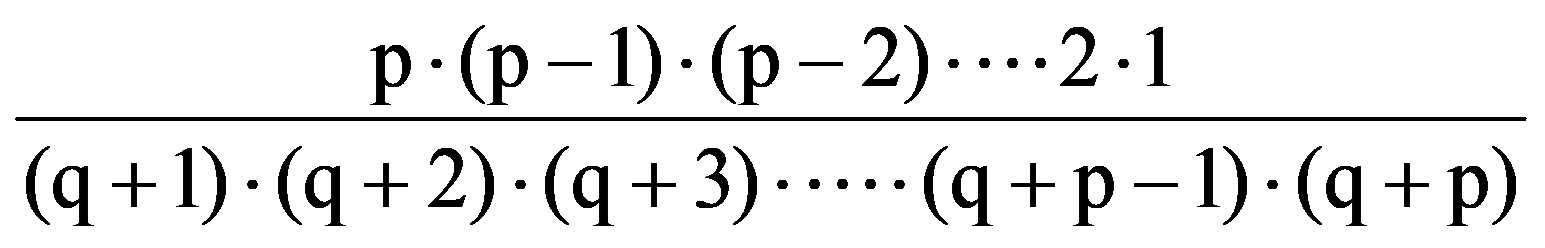
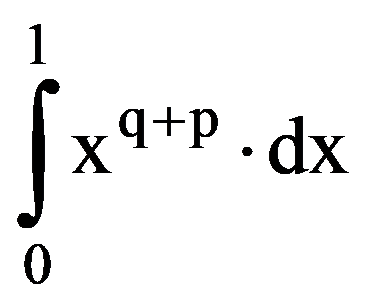
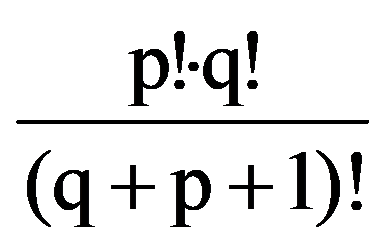
From the equalities (3) and (7) it follows that:

I(p,q)=

. (8)

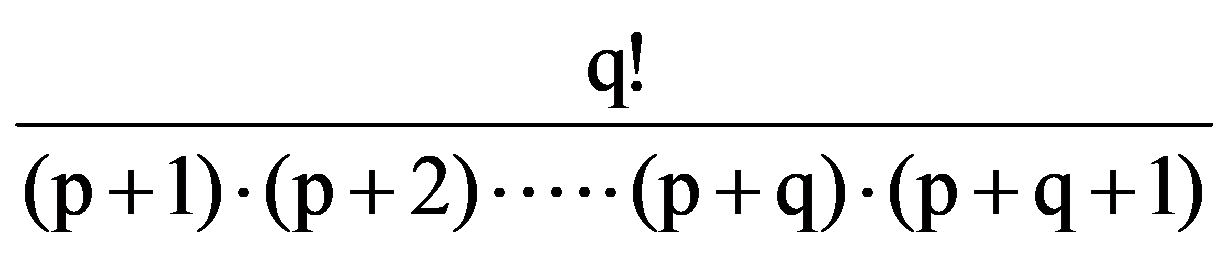
Now, from the equalities (7) and (8), obtain the equalities obvious: for every p, q N ,

=

=

. (9)

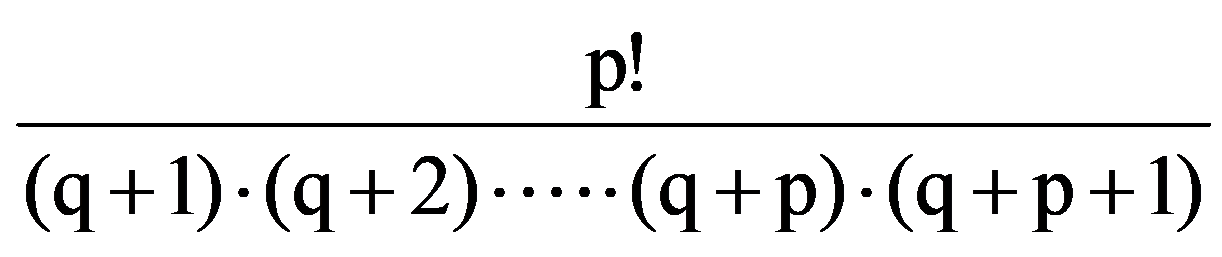
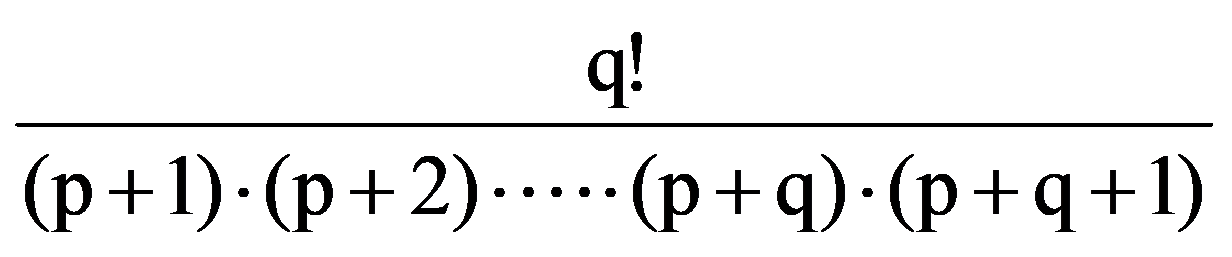
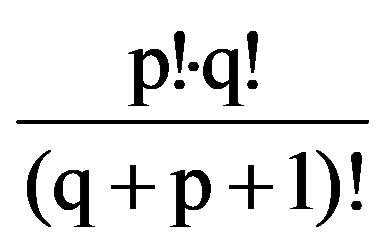
On the other hand, from the equalities (2) and (7) it follows that:

=

I(p.q)=

C

=

C

. (10)

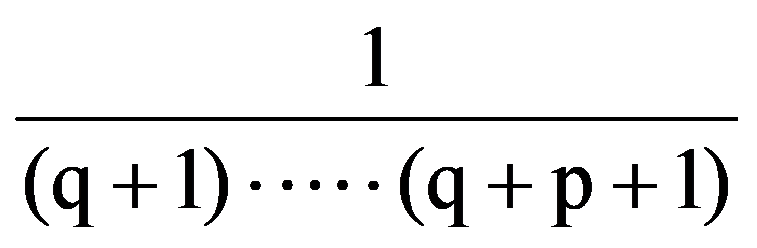
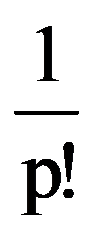
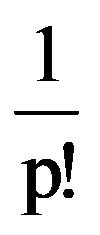
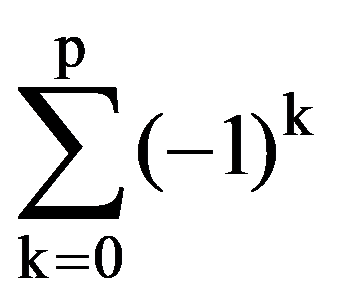
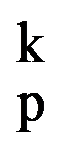
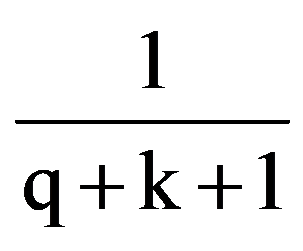
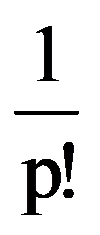
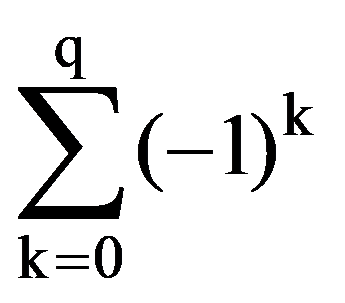
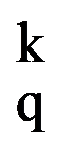
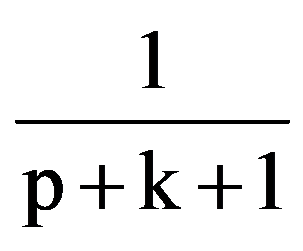
Analogous, obtain that:

=

I(q,p)=

C

=

=

-

+

-

+(-1)^q-1

+(-1)^q

=

C

. (10)

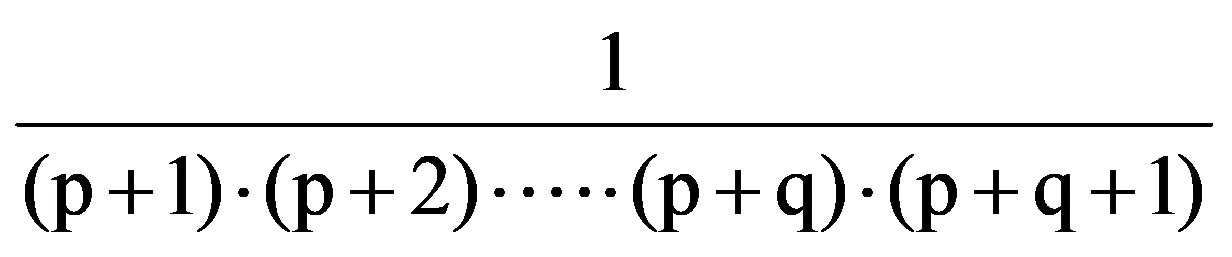
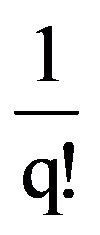
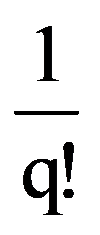
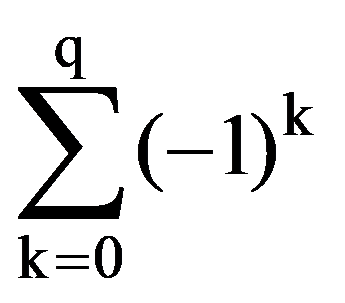
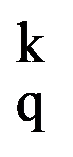
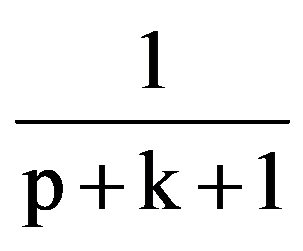
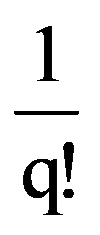
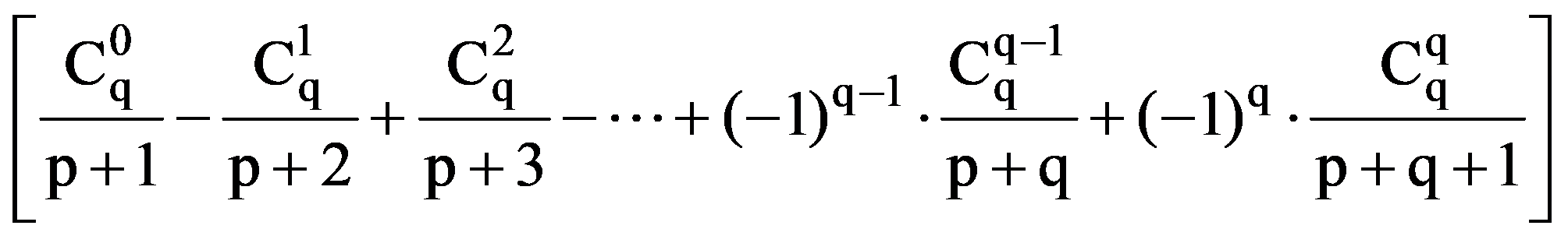
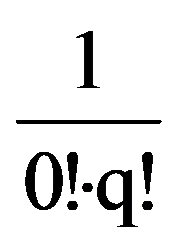
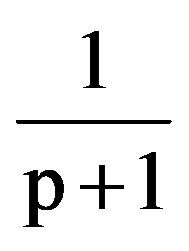
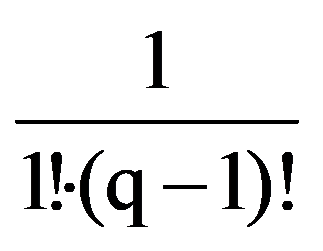
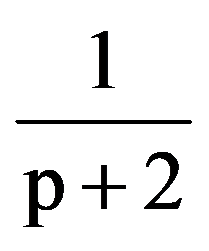
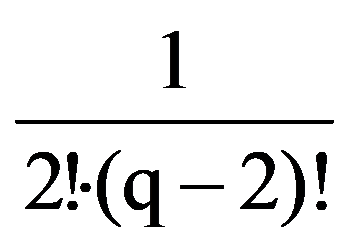
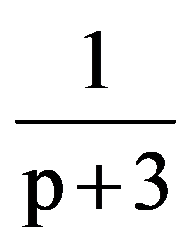
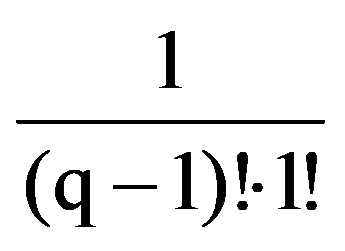
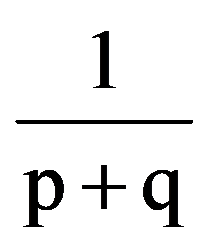
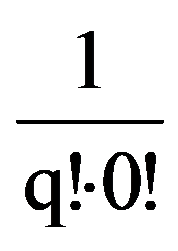
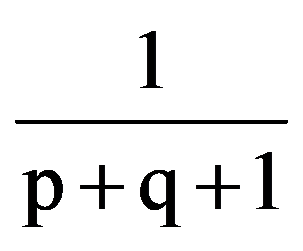
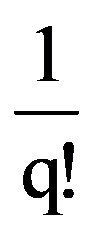
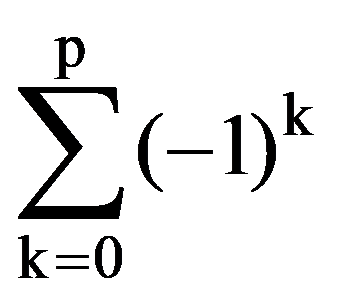
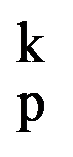
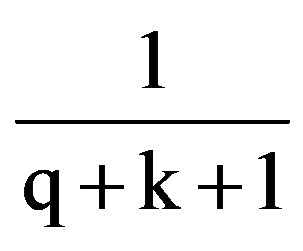
Consequences (1)

The theoretical results obtained above are entails two consequences important data in particular cases.

1) For every p, n N ,

I(p,n)=

=

=

=

C

=

C

=

=

=I(n,p). (11)

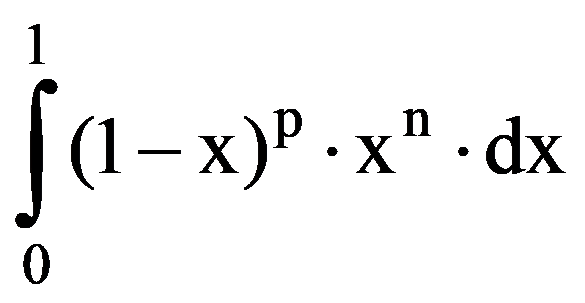
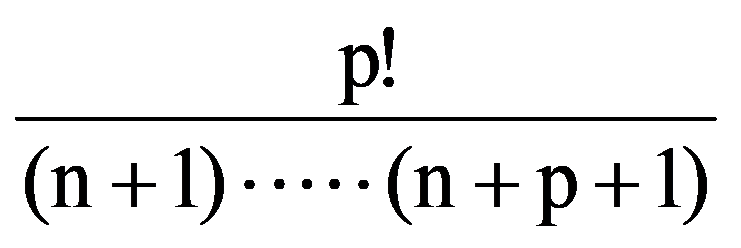
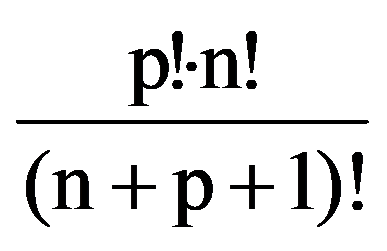
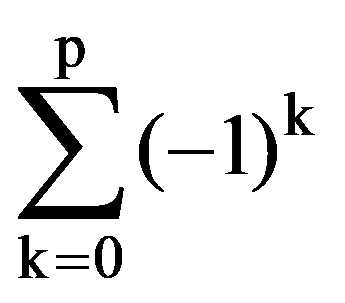
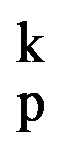
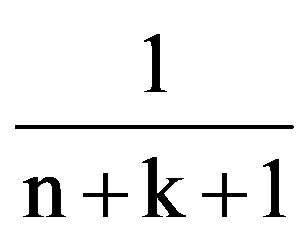
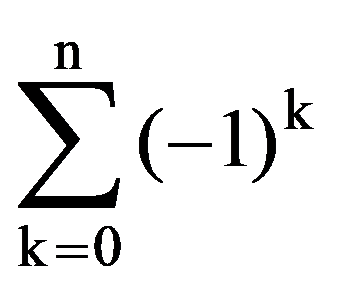
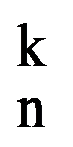
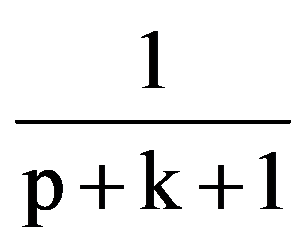
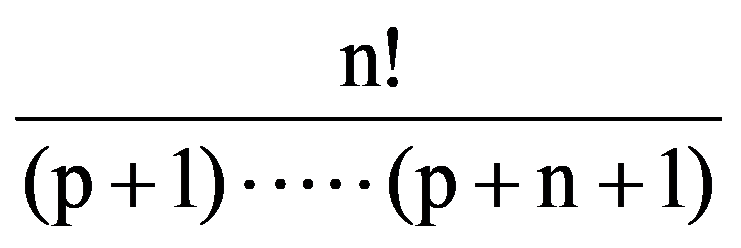
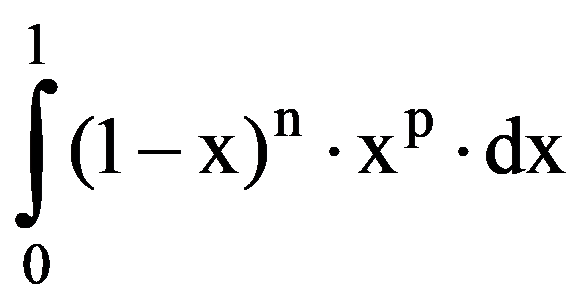
Therefore,

=

I(p,n)=

C

=

-

+

+(-1)^p-1

+(-1)^p

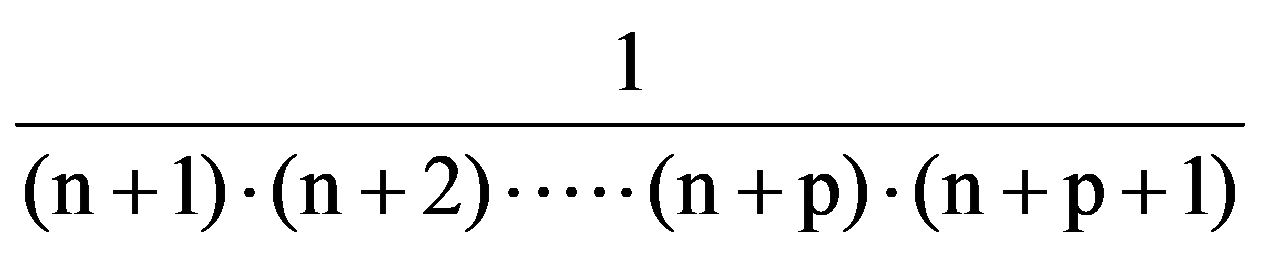
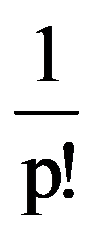
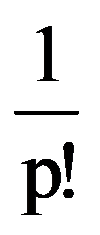
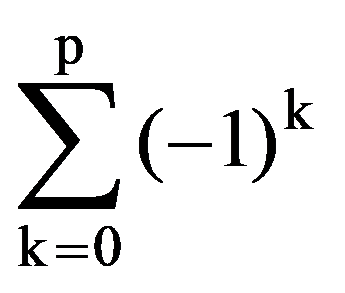
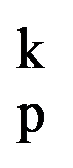
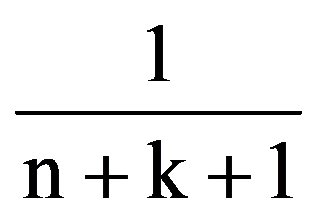
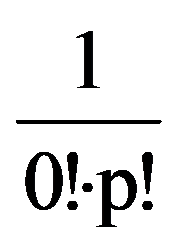
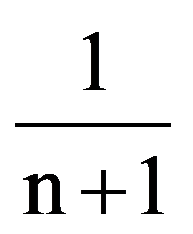
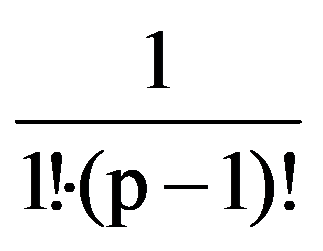
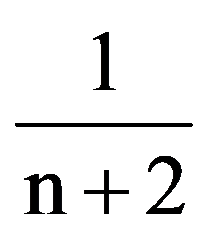
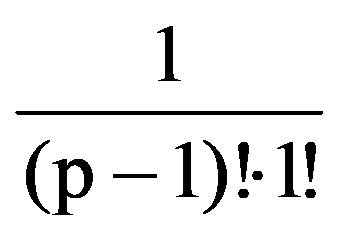
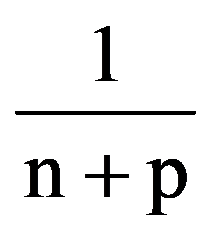
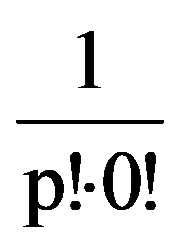
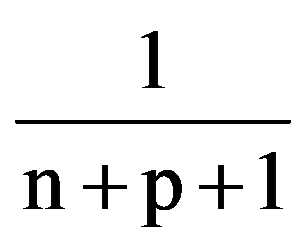
and

=

C

=

I(n,p)=

. (11)

2) For every n N ,

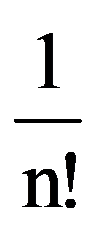
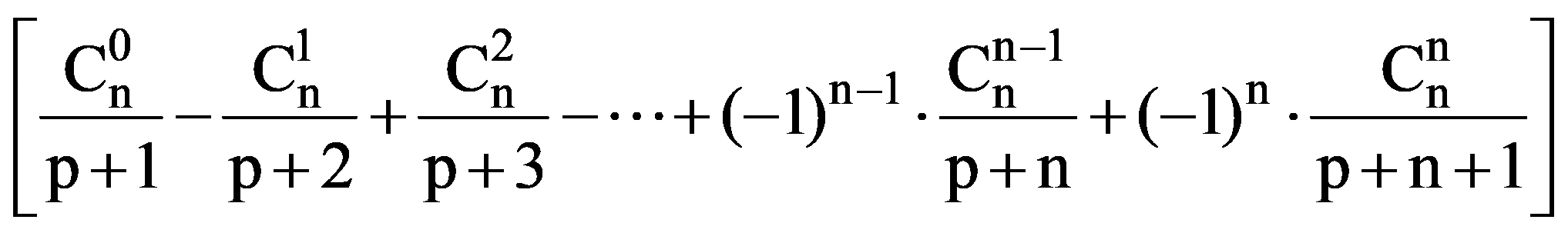
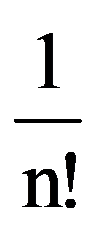
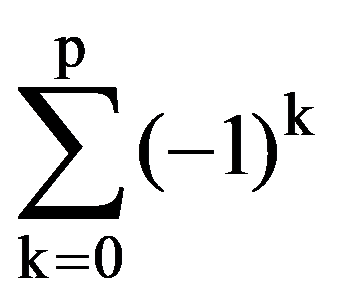
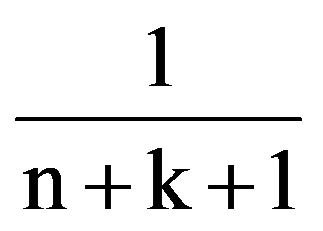
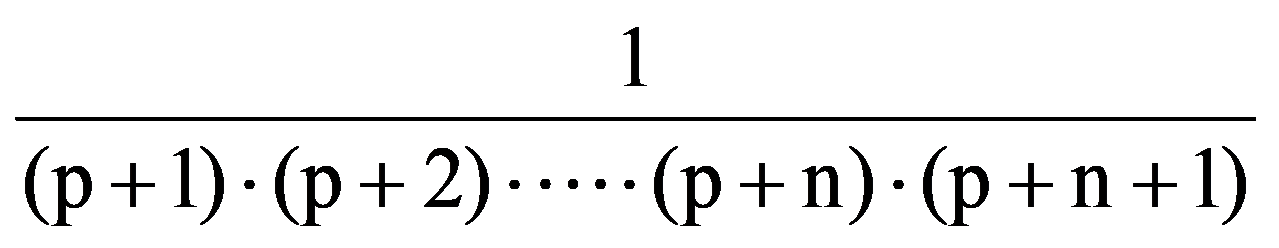
I(n,n)=

=

=

=

C

. (12)

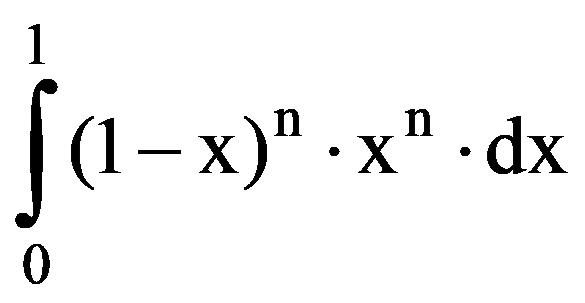
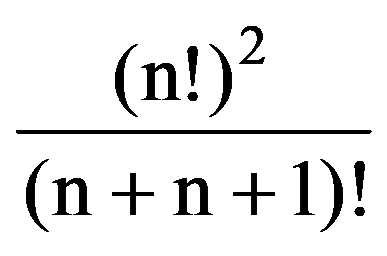
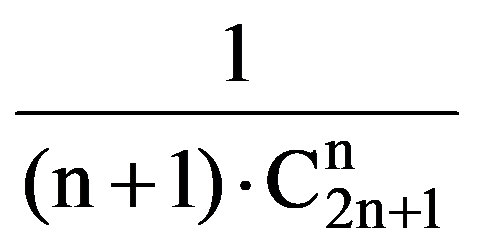
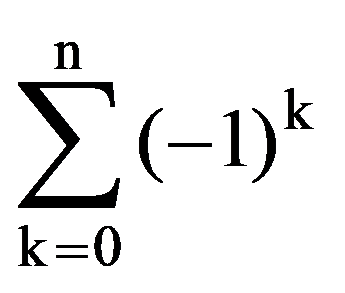
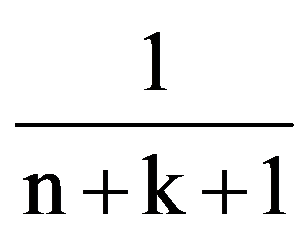
Generalizations

Now we generalize the results from the first two paragraphs. Thus, let be p, q N , a, b R , with ab and consider the definite integral:

J(p.q)=

. (13)

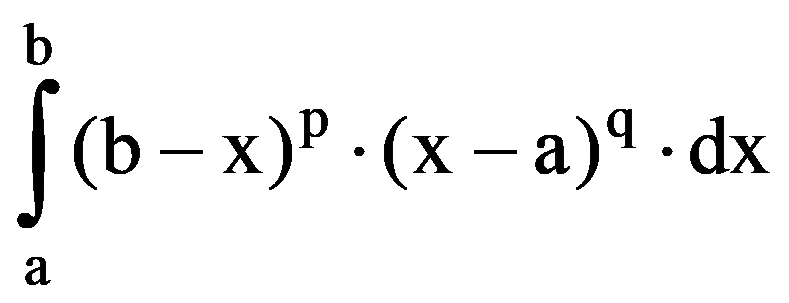
Using the binomial theorem (of Newton), we obtain that, for every p, q N and every a, b R , with ab:

J(p.q)=

=

=

=

. (14)

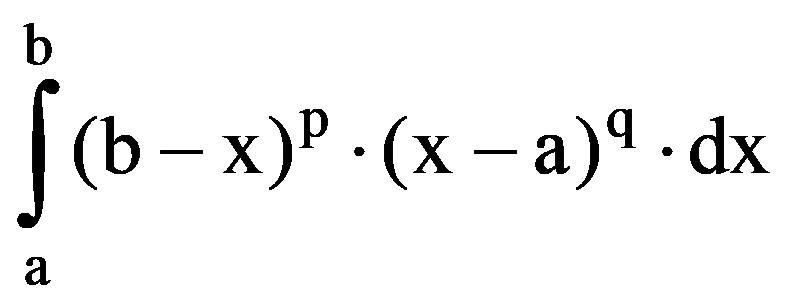
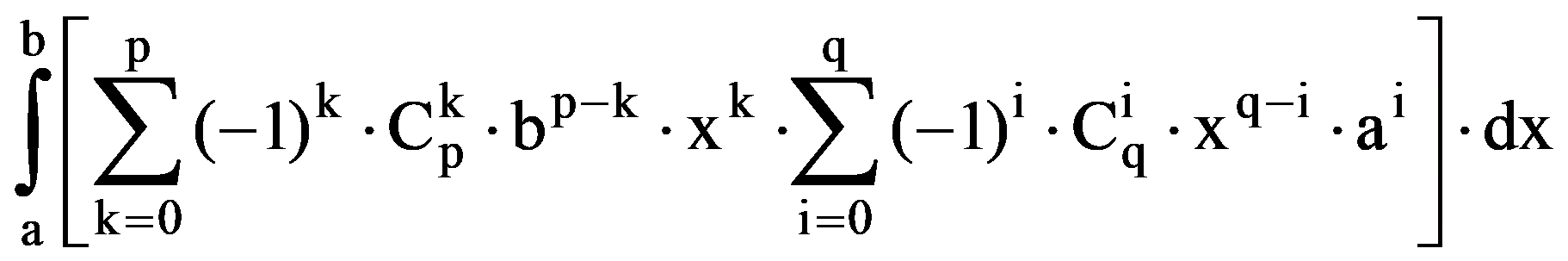
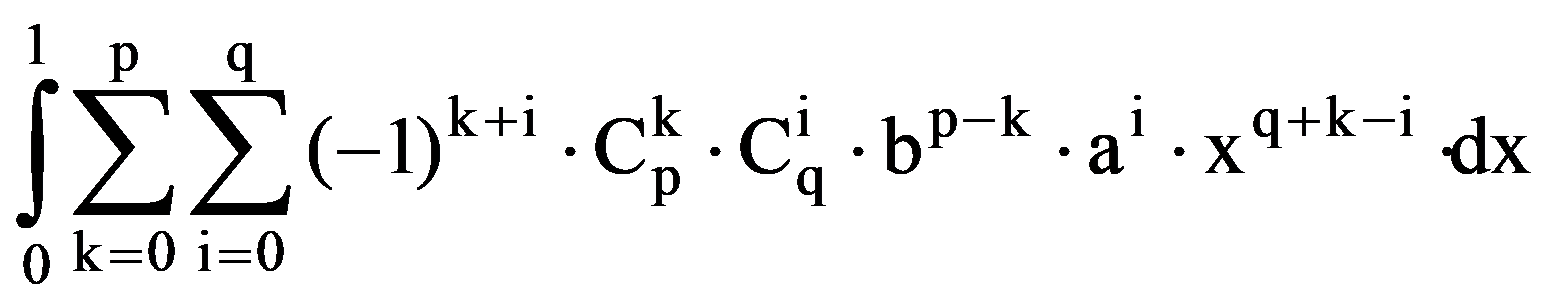
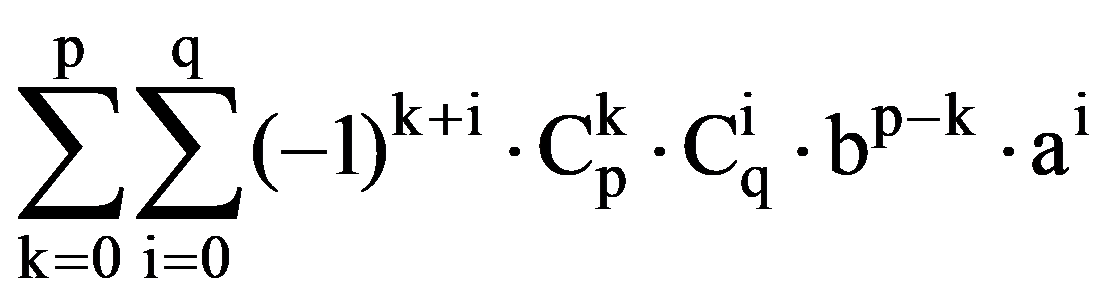
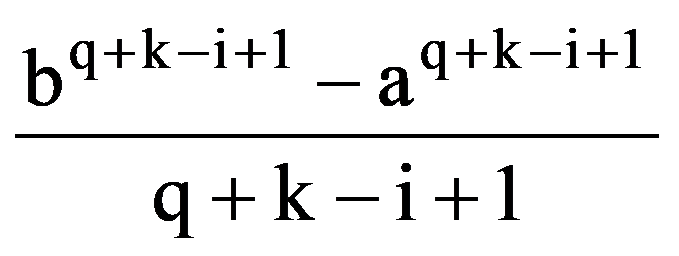
But, by making change of variable x=a+b-y, obtain that, for every p, q N and a, b R , with ab:

J(p.q)=-

=

=J(q,p). (15)

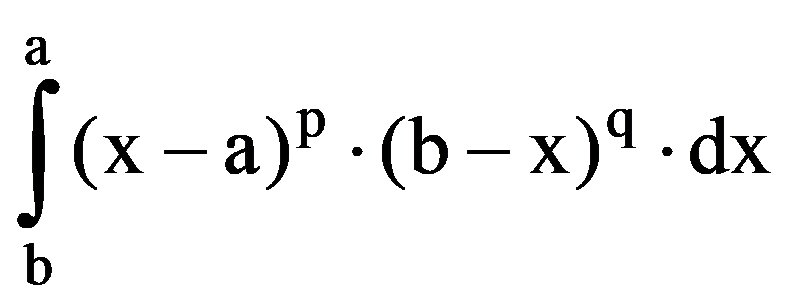
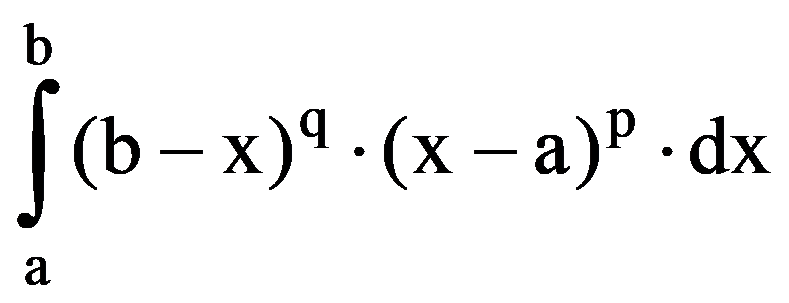
By proceeding as above, obtain that, for every p, q N and every a, b R , with ab:

J(q,p)=

. (16)

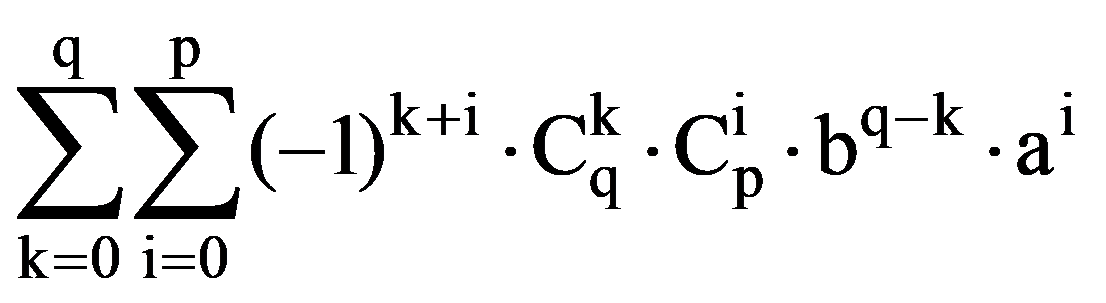
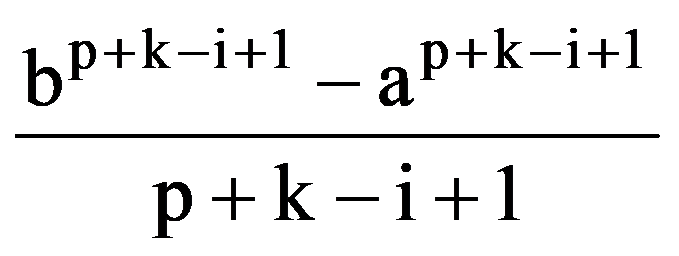
From the equalities (14), (15) and (16) it follows that, for every p, q N and every a, b R , with ab:

=

. (17)

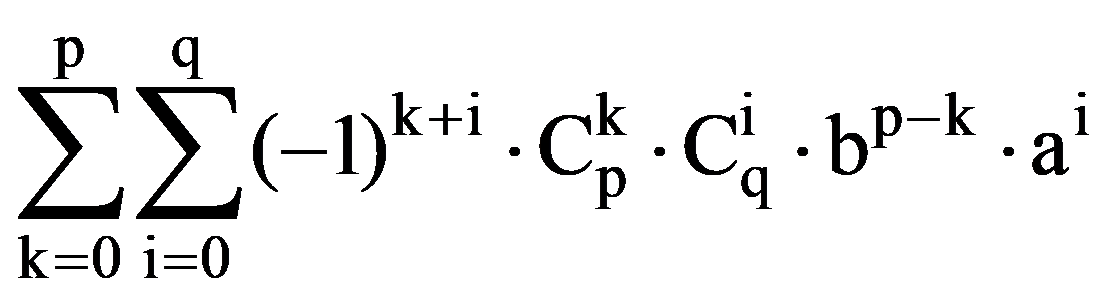
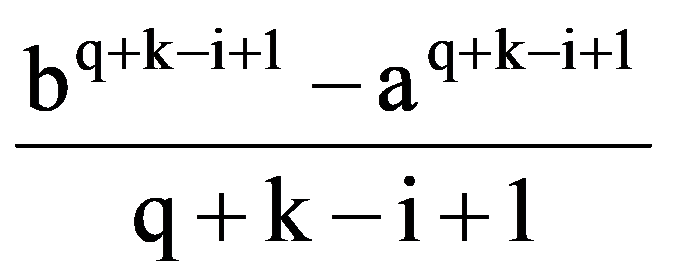
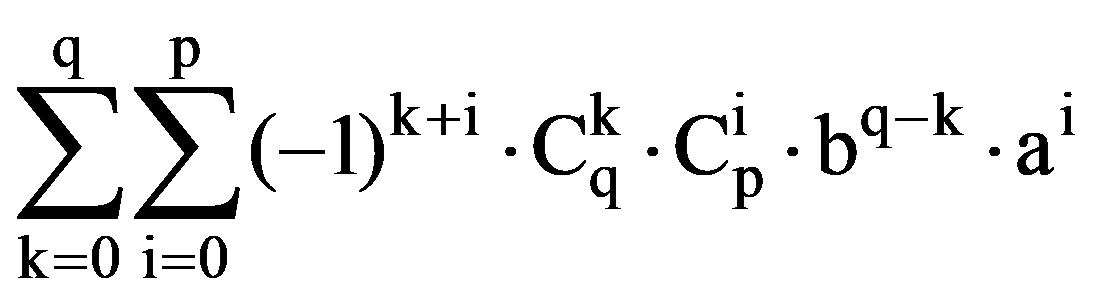
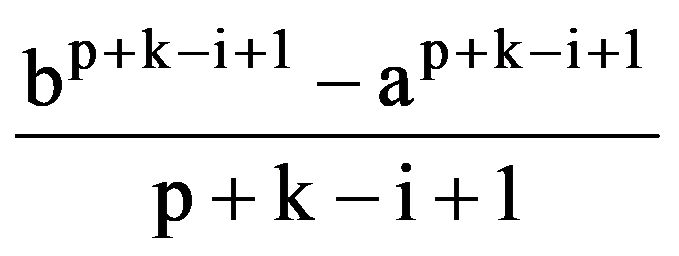
On the other hand, integrating by parts, obtain that, for every p, q N and every a, b R , with ab:

J(p.q)=

+

=

J(p-1,q+1). (18)

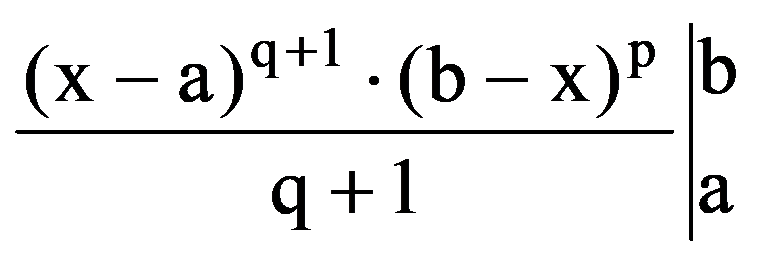
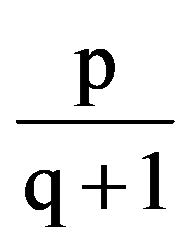
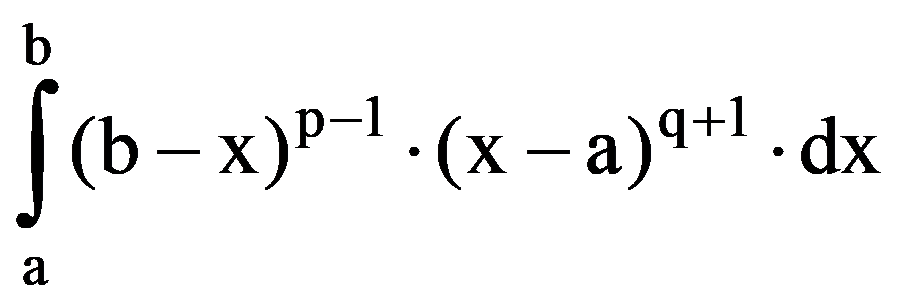
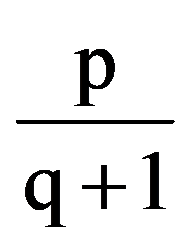
From the equalities (18) it follows that, for every p, q N and every a, b R , with ab:

J(p,q)=

J(p-1,q+1)=

=

J(0,q+p)

=

=

(b-a)^q+p+1=

(b-a)^q+p+1. (19)

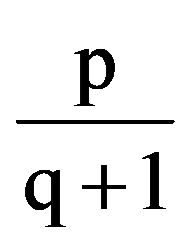
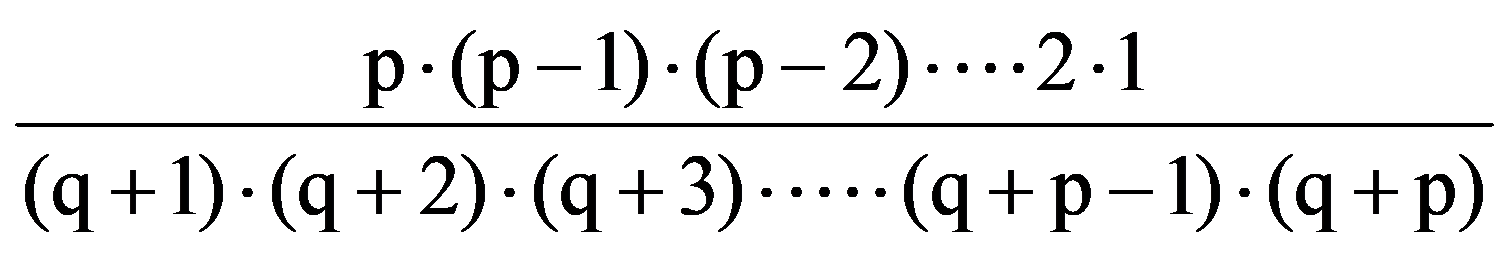
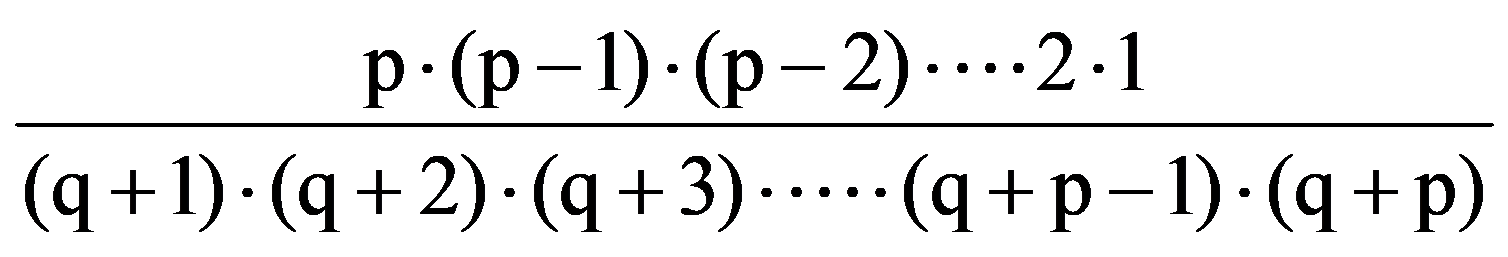
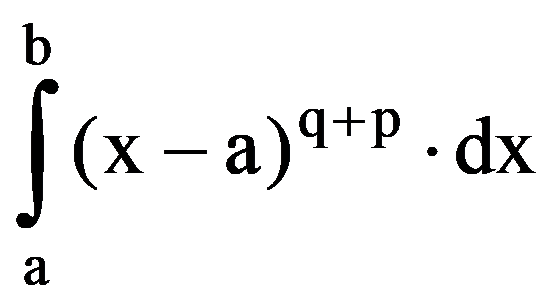
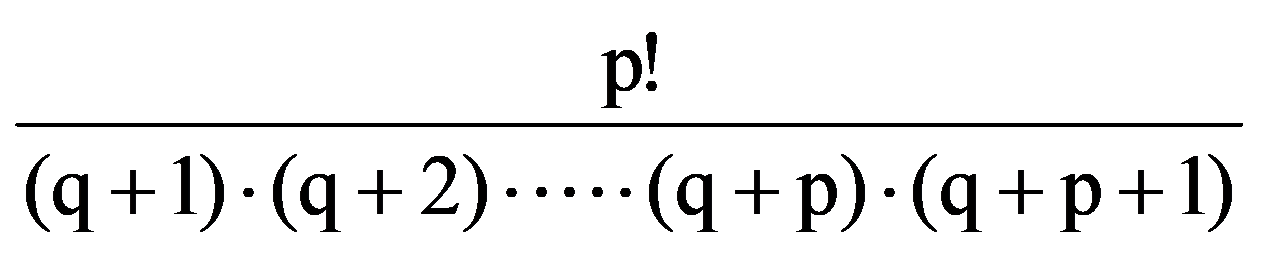
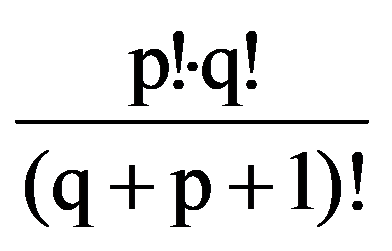
From the equalities (15) and (19) it follows that, for every p, q N and every a, b R , with ab:

J(p,q)=

(b-a)^q+p+1. (20)

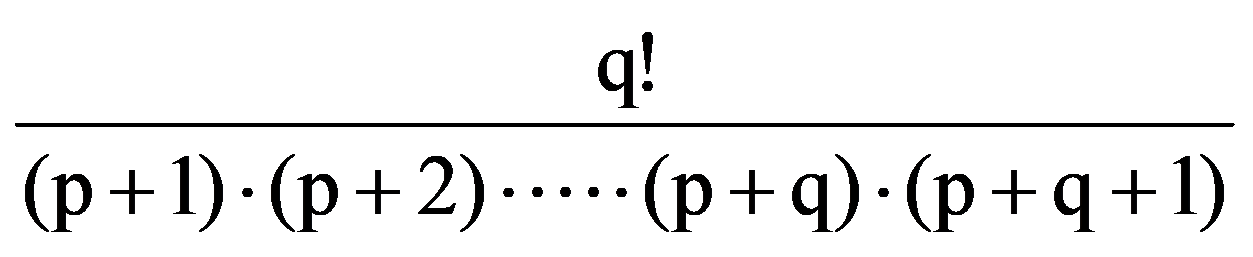
Therefore, from the equalities (19) and (20), obtain again the equalities (9).

From the equalities (14) şi (19) it follows that, for every p, q N and every a, b R , with ab:

=

J(p.q)

=

. (21)

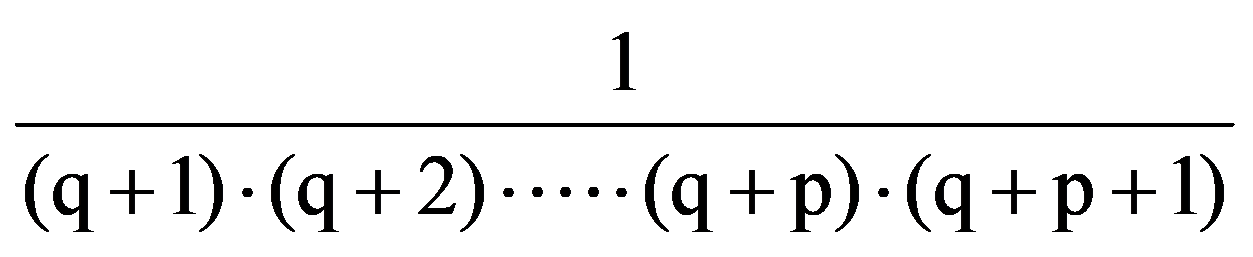
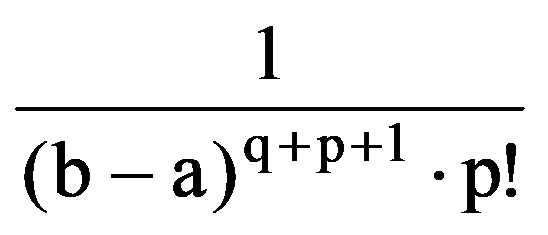
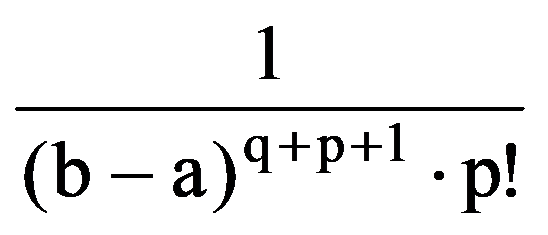
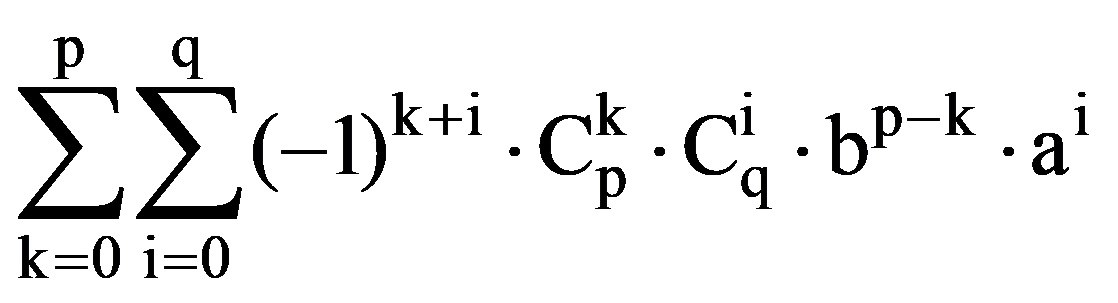
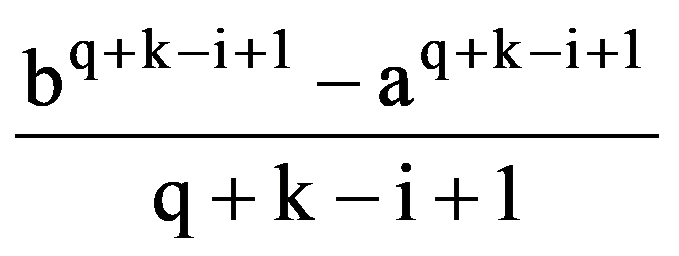
Analogous, obtain that, for every p, q N :

=

J(q,p)=

=

. (21)

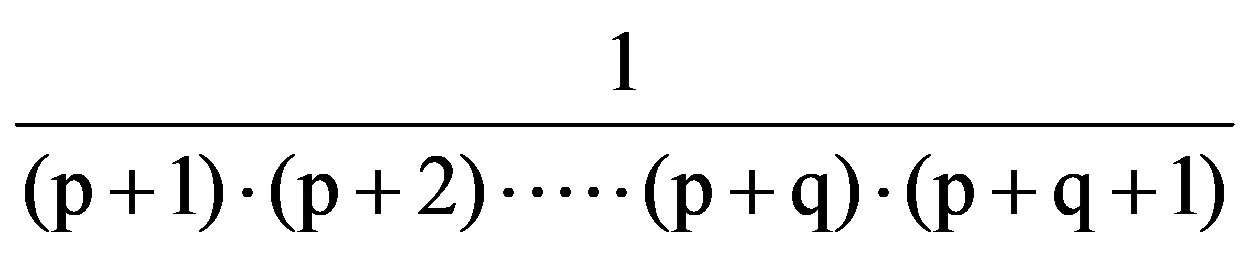
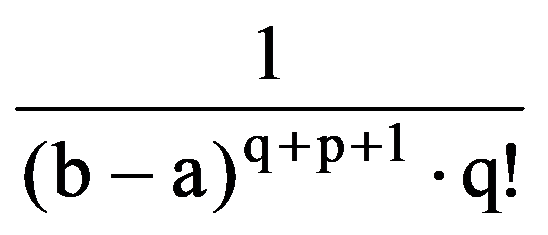
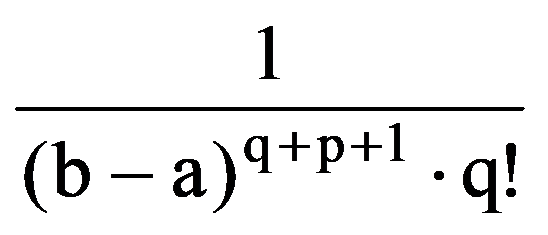
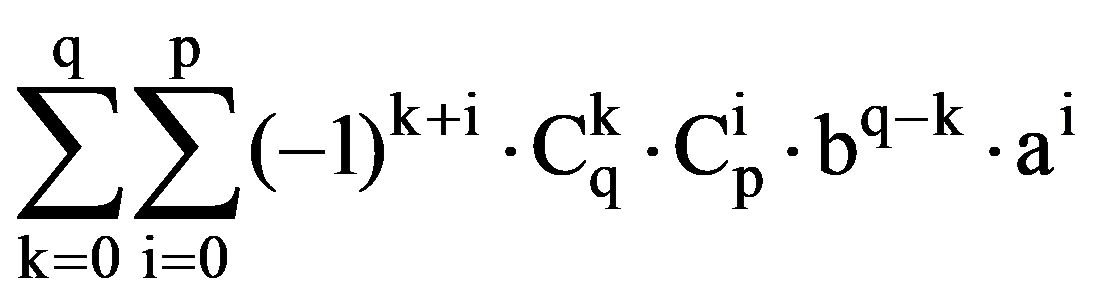
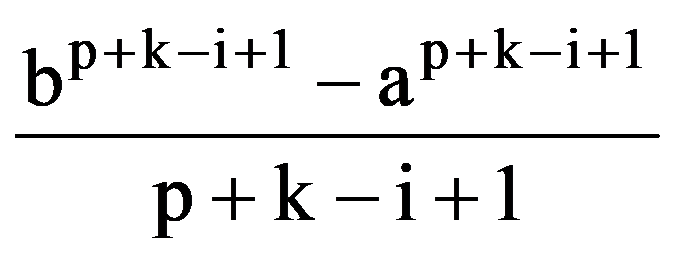
Consequences (2)

Now, we present two consequences of the results of the previous paragraph, obtained on particular cases.

1) For every p, n N and every a, b R , with ab:

J(p,n)=

=

(b-a)^n+p+1=

(b-a)^n+p+1

=

=

=

(b-a)^n+p+1=

=J(n,p). (22)

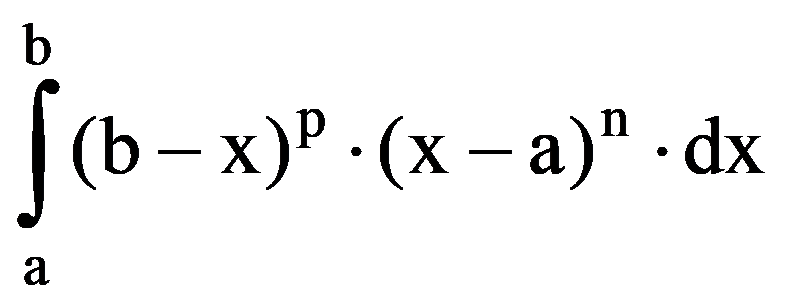
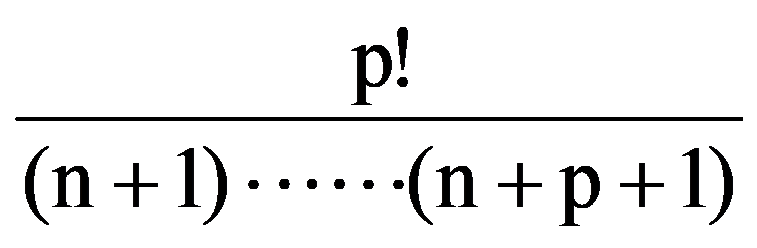
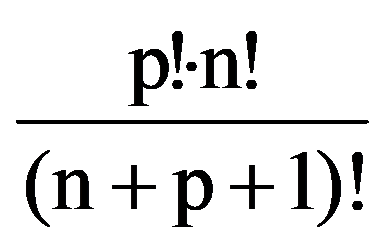
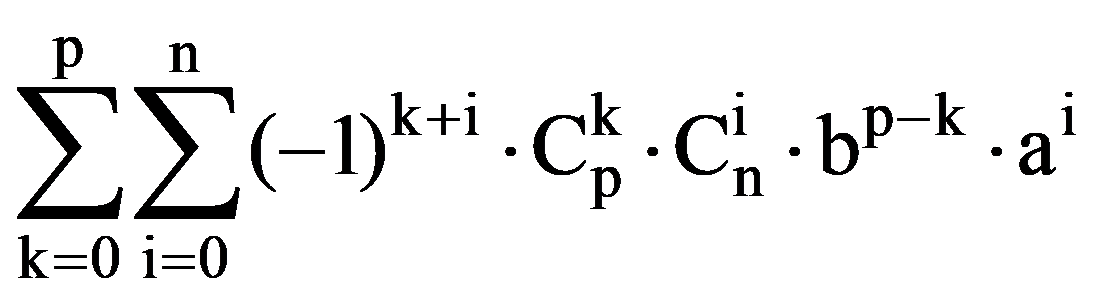
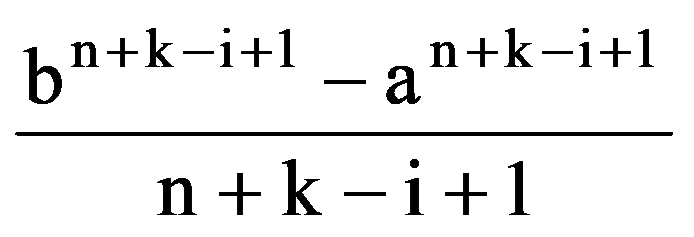
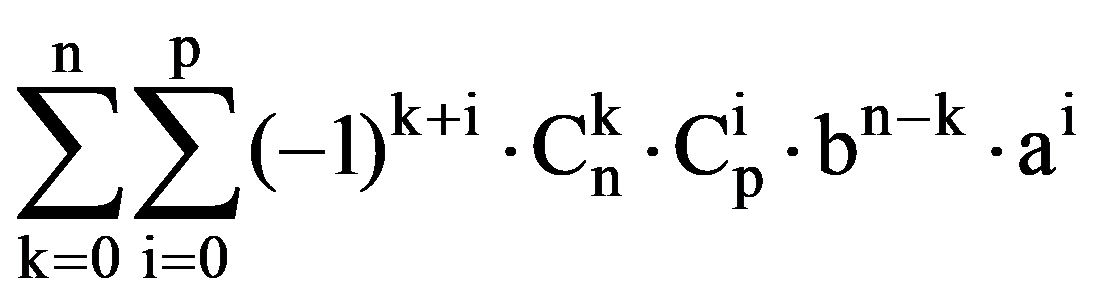
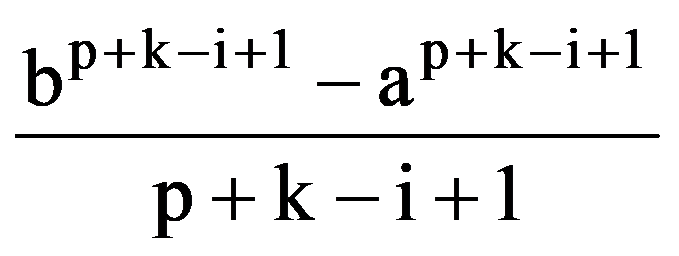
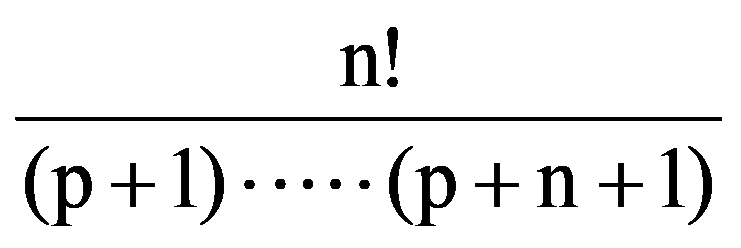
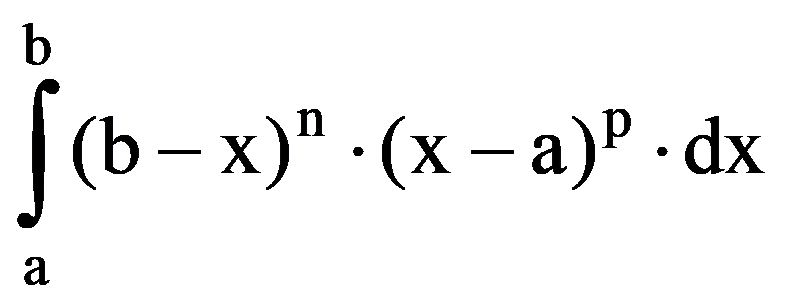
Therefore,

=

J(p,n)

=

=

=

J(n,p)=

. (22)

2) For every n N , and every a, b R , with ab:

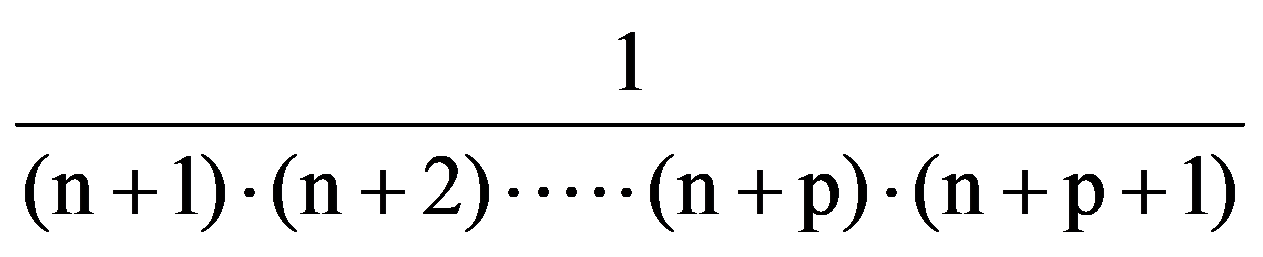
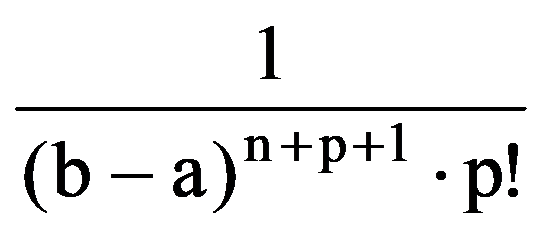
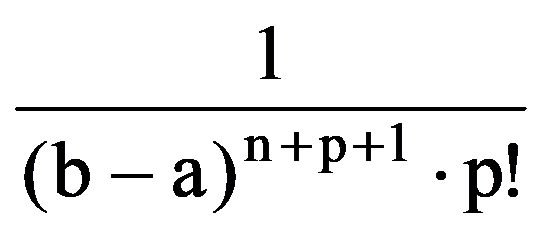
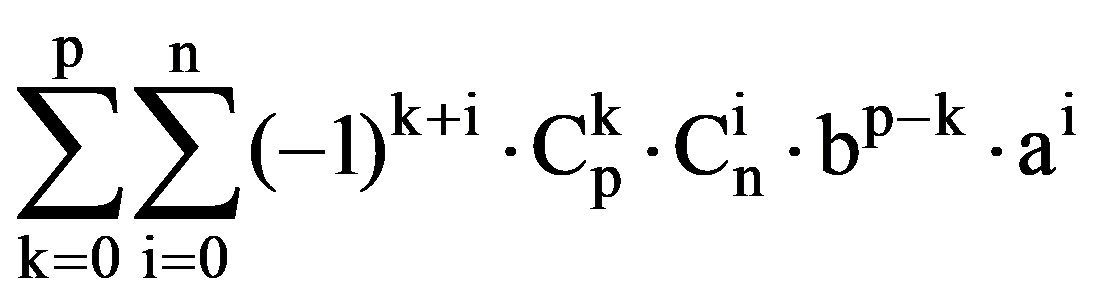
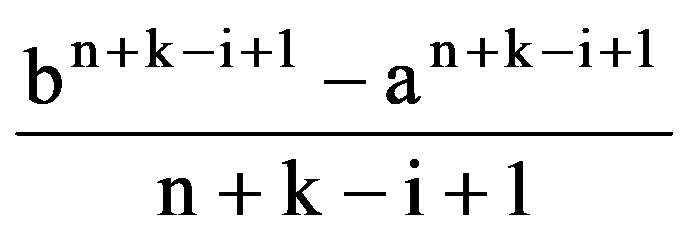
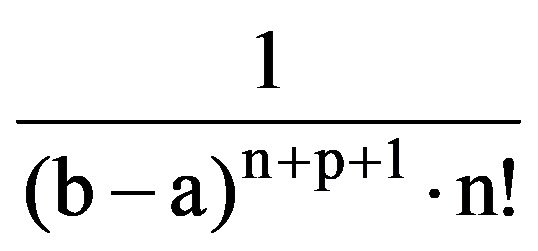
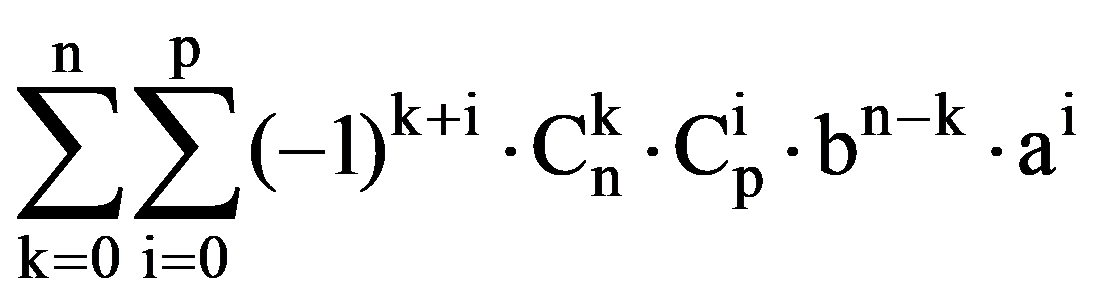
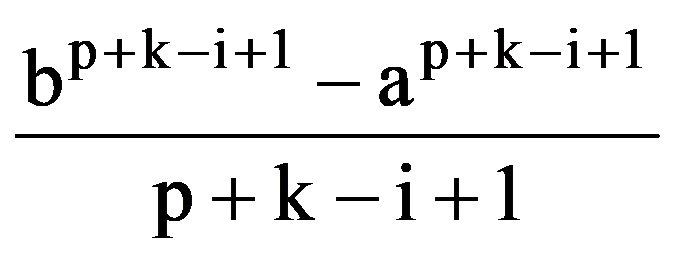
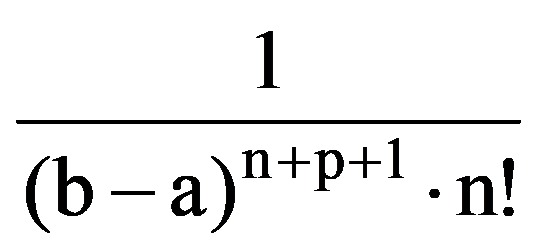
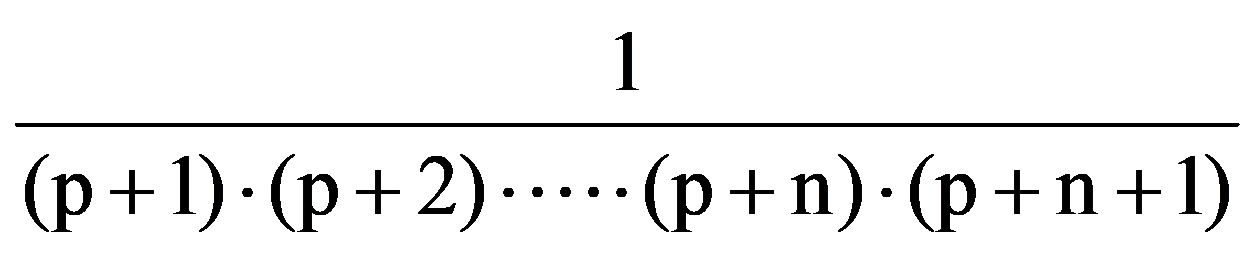
J(n,n)=

=

(b-a)²ⁿ⁺¹=

(b-a)²ⁿ⁺¹

=

(b-a)²ⁿ⁺¹=

. (23)

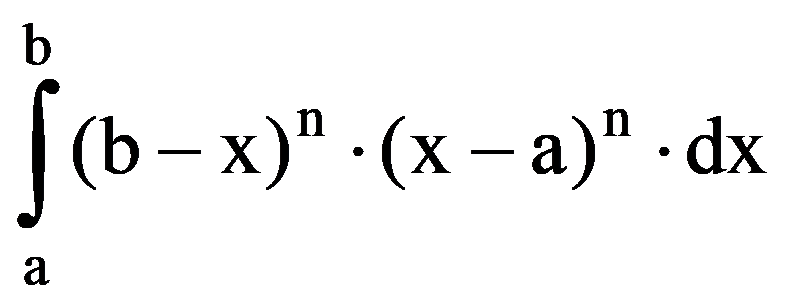
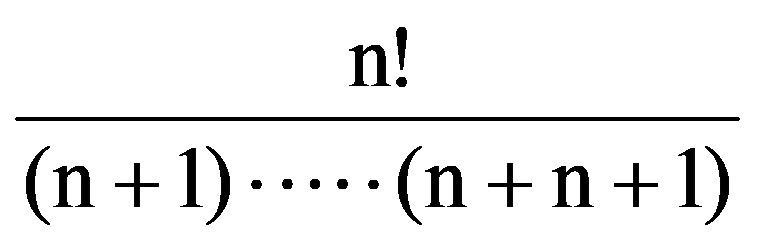
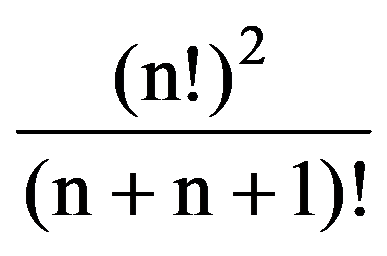
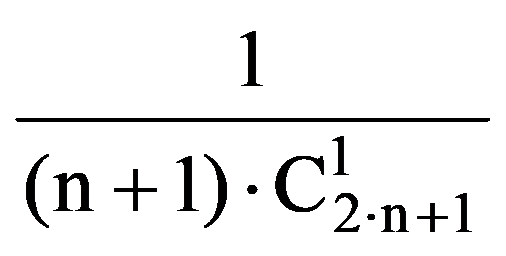
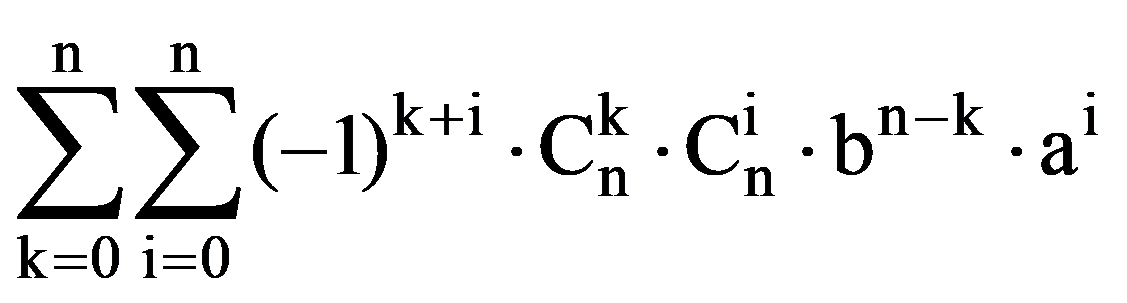
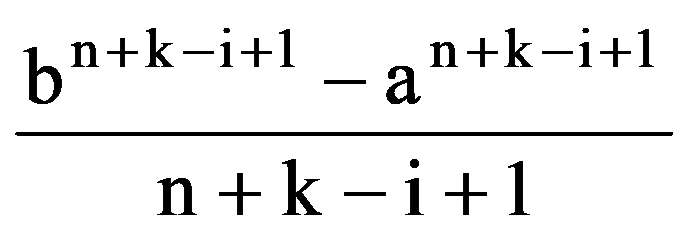
In particular,

3) For every n N ,

J(n,n)=

=

=

2²ⁿ⁺¹

=

2²ⁿ=

2²ⁿ. (24)

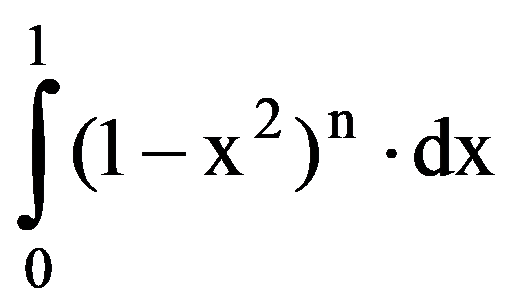
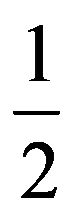
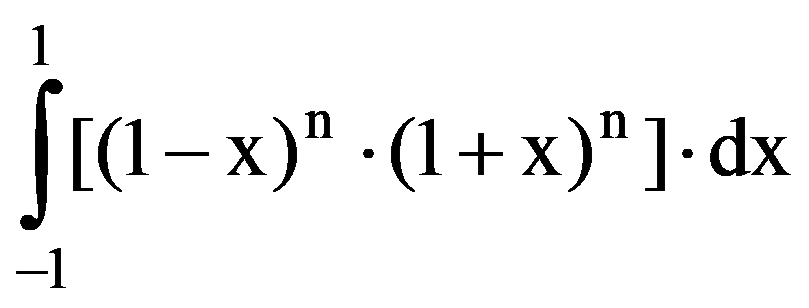
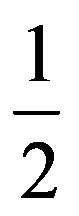
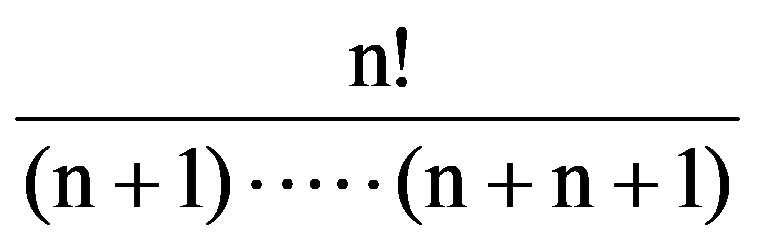
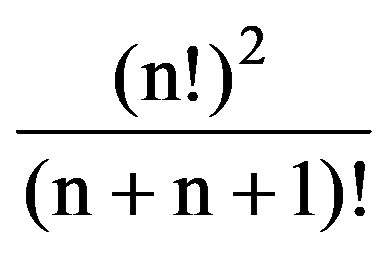
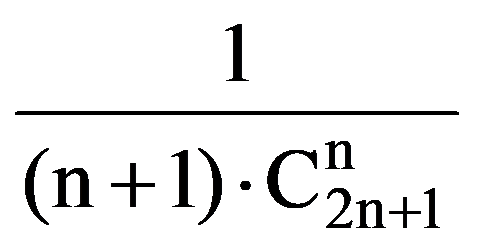
So, the sequences (J(n,n))_n_N above is decreasing and has limits 0.

Applications

6.1 The calculation of some limits of sequences

Using those presented in previous paragraphs we can calculate a series of sequences limits. Thus, we can show that the following equalities hold:

1)

=

, p, q N , pq.

2)

=

, p, q, r N , prq.

3)

=

.

4)

=

, p, q, r, s N , prsq.

5)

=

.

6)

=

.

7)

=

.

8)

=

.

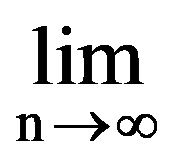
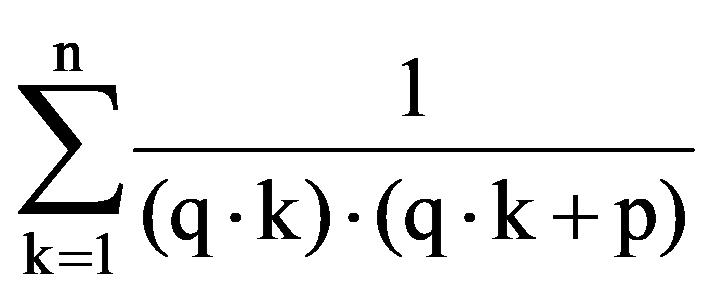
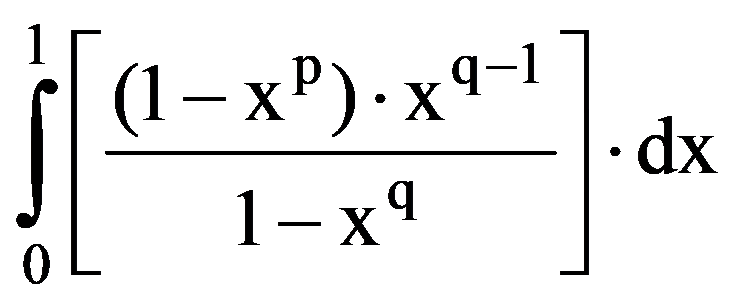
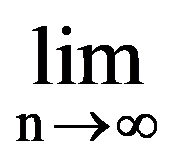
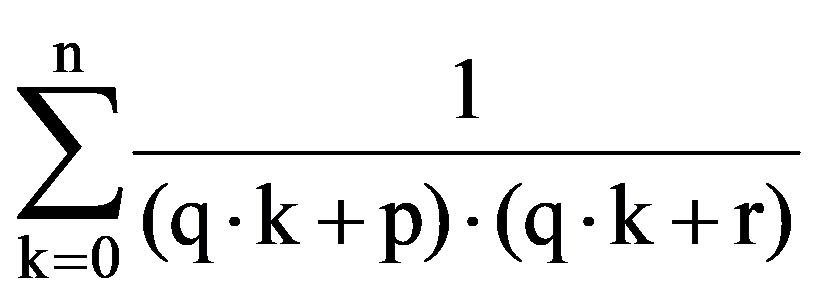
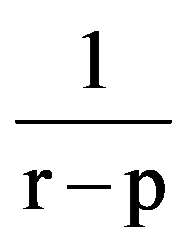
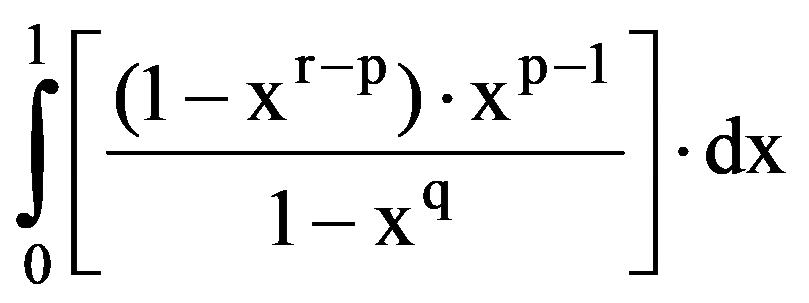
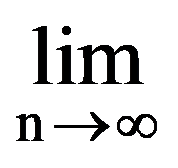
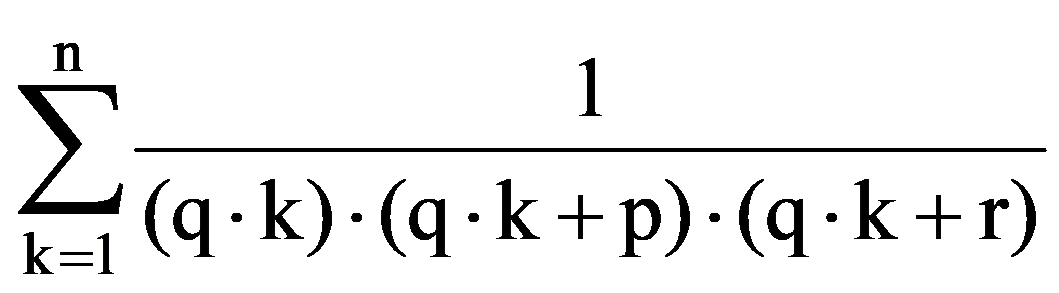
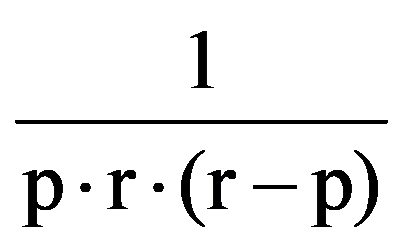
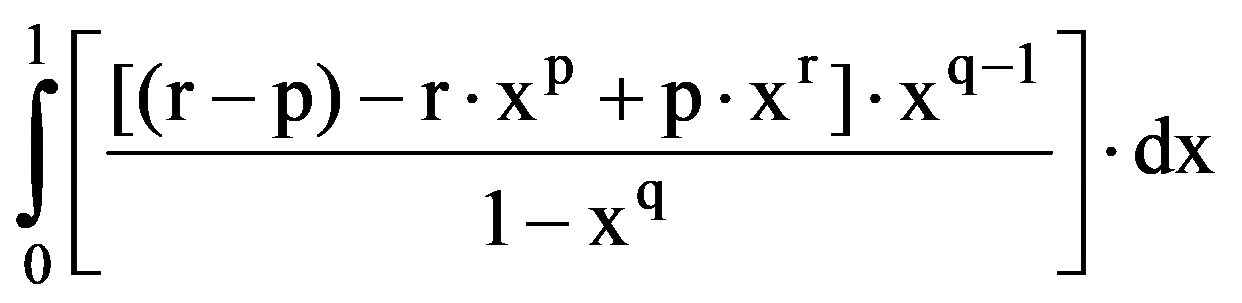
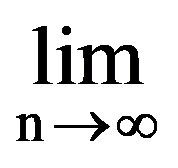
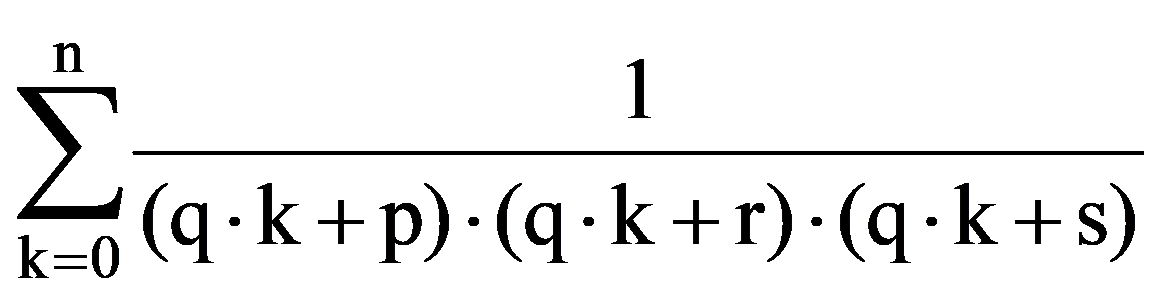
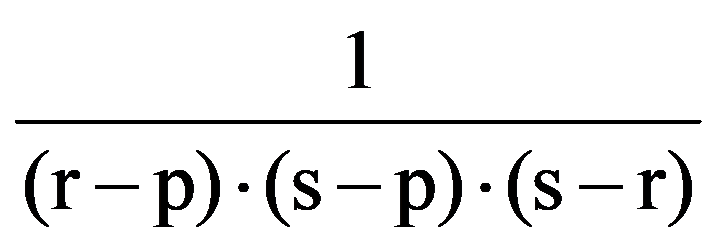
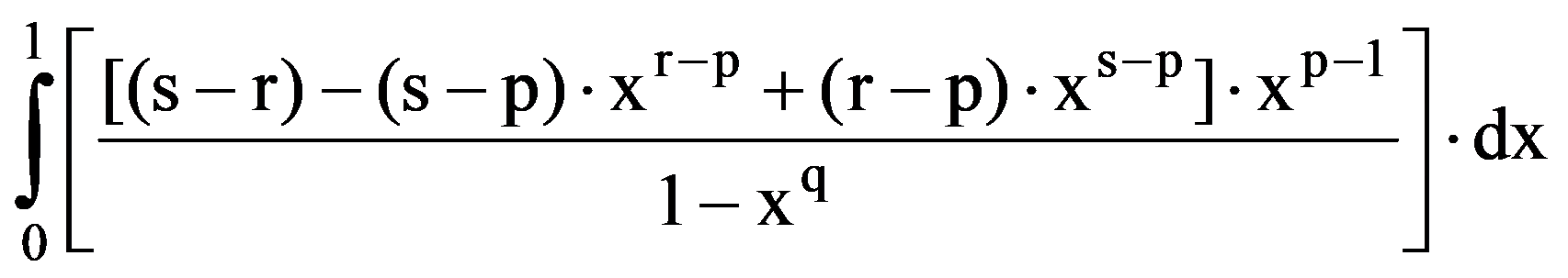
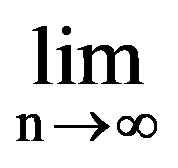
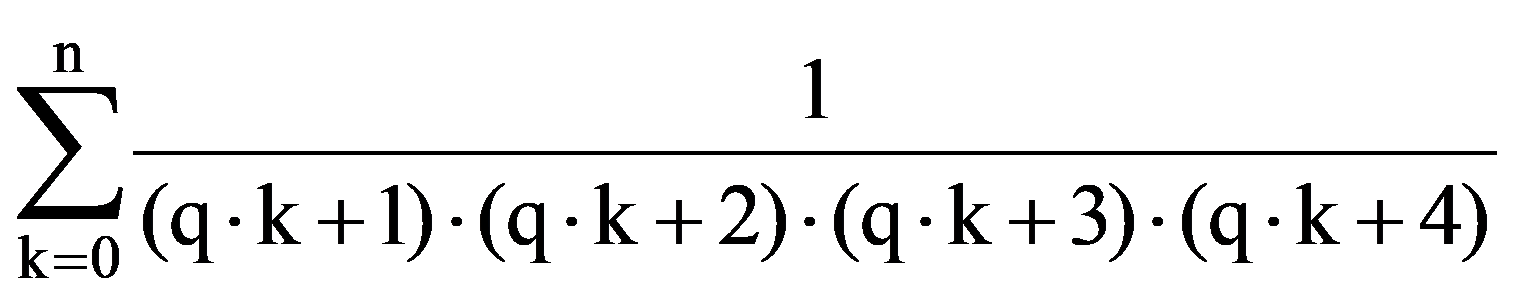
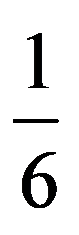
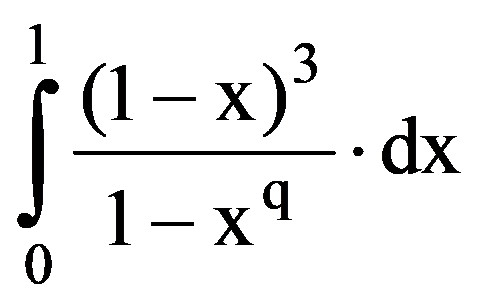
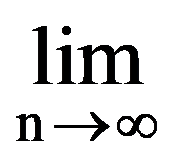
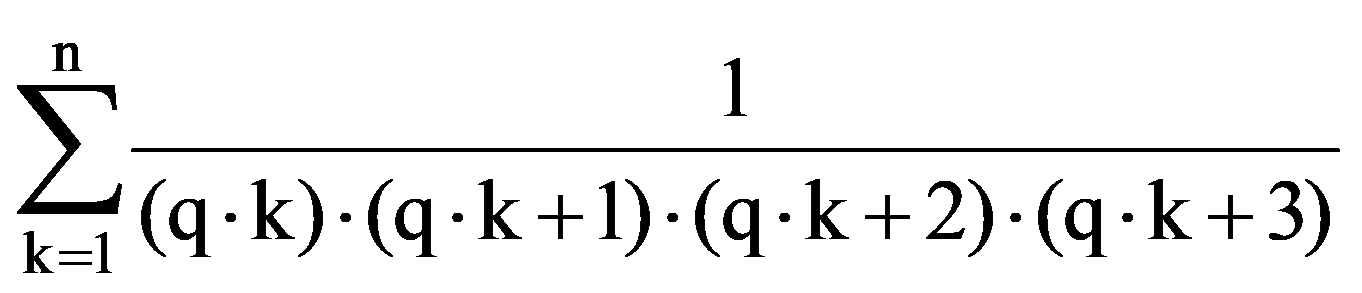
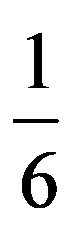
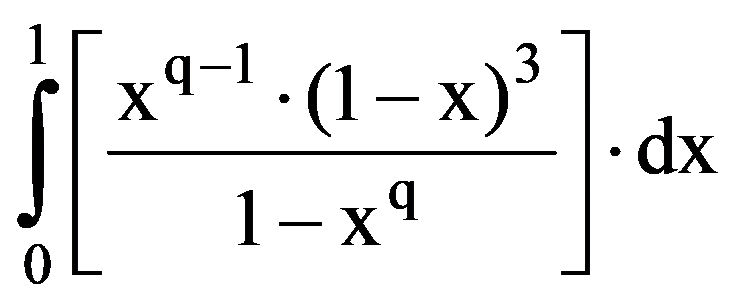
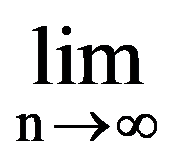
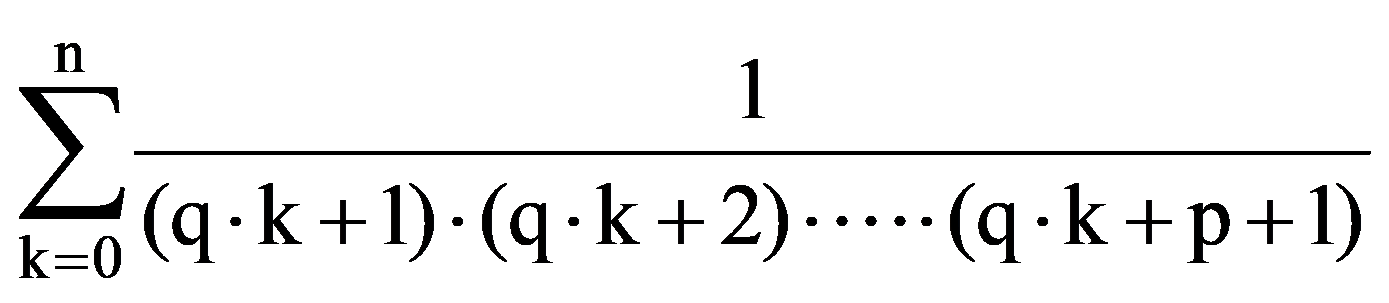
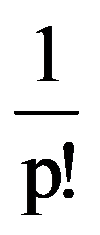
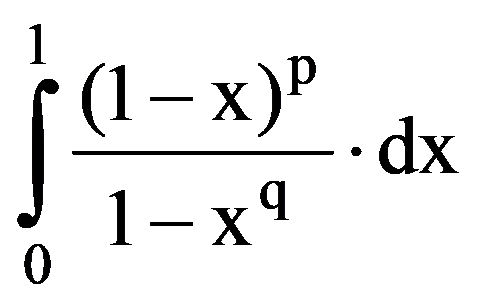
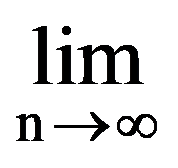
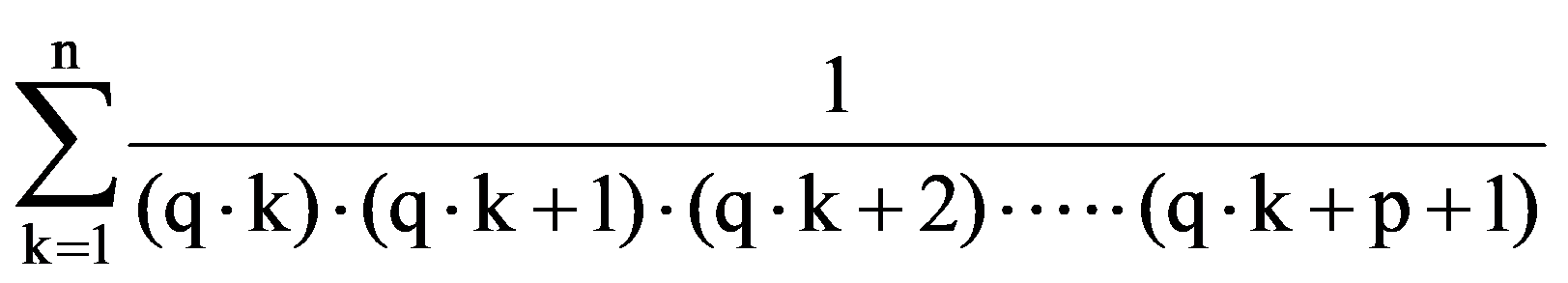
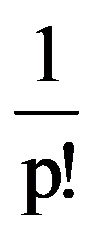
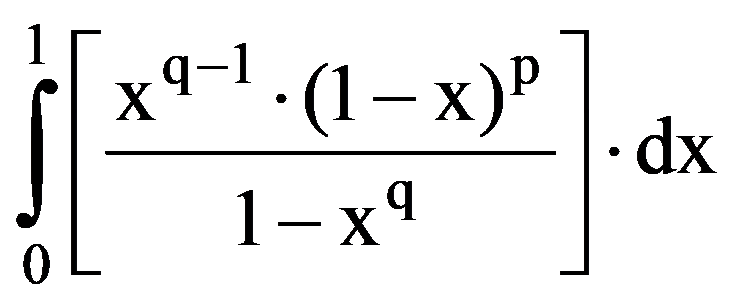
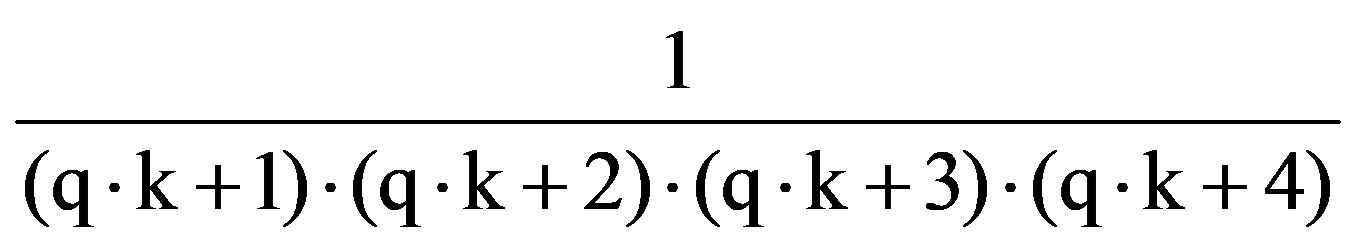
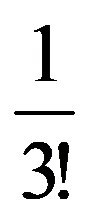
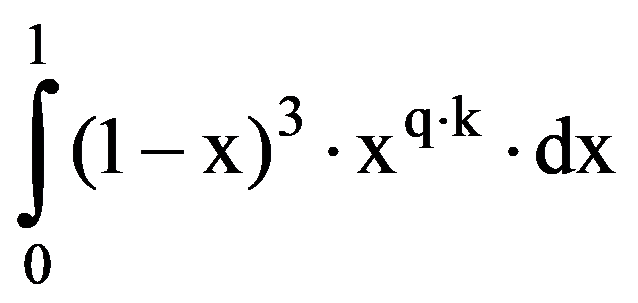
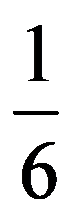
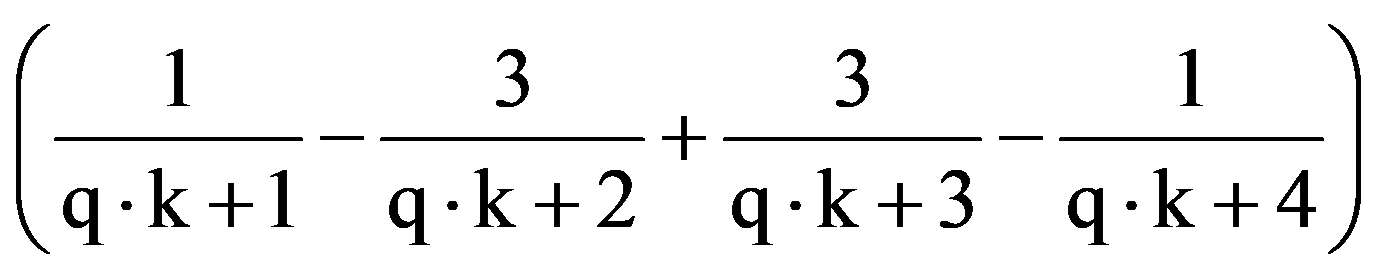
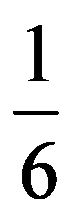
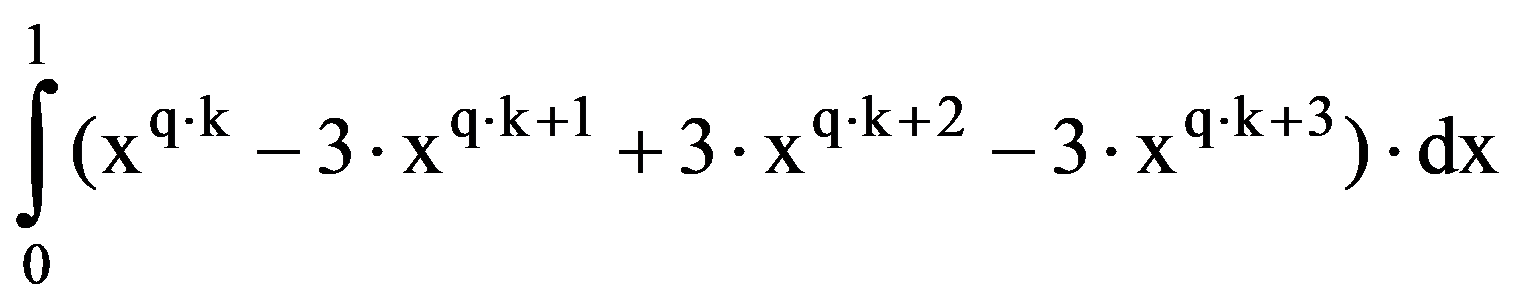
To prove Exercise 5): For every k N , p=3, from the equalities (10) it follows that:

=

=

=

.

So,

=

=

=

=

=

.

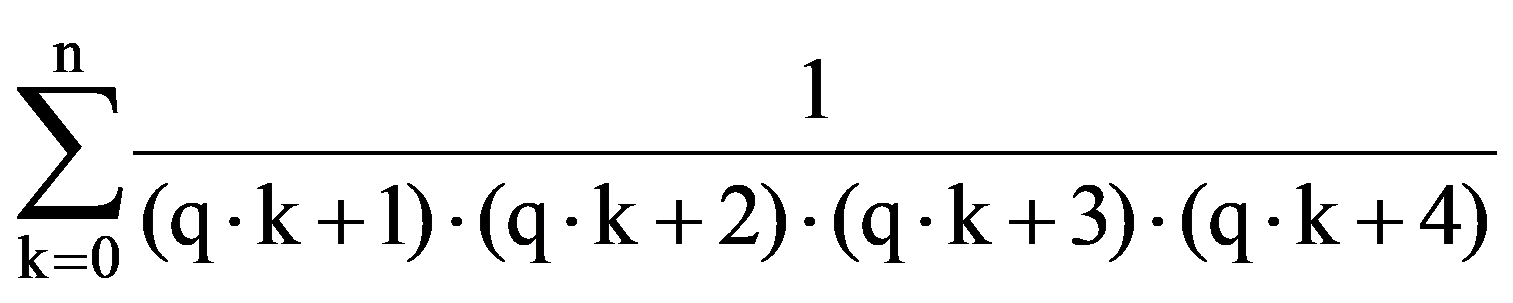
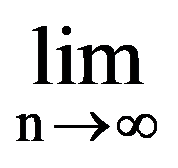
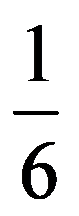
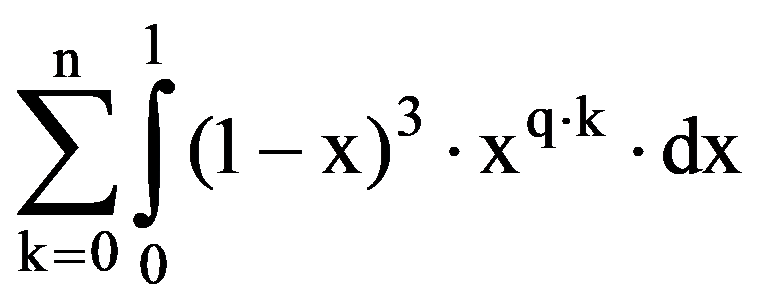
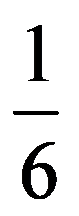
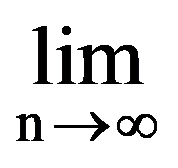
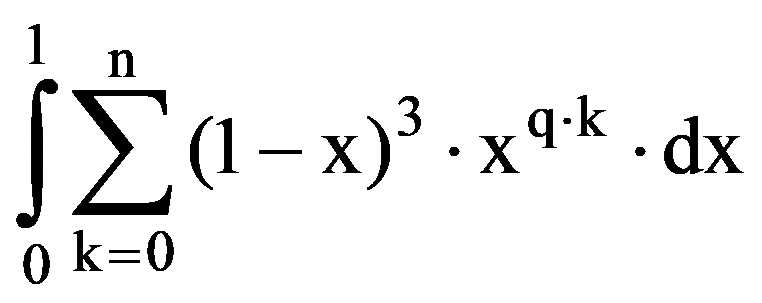
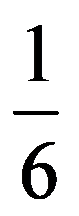
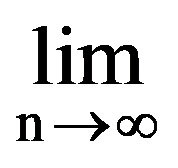
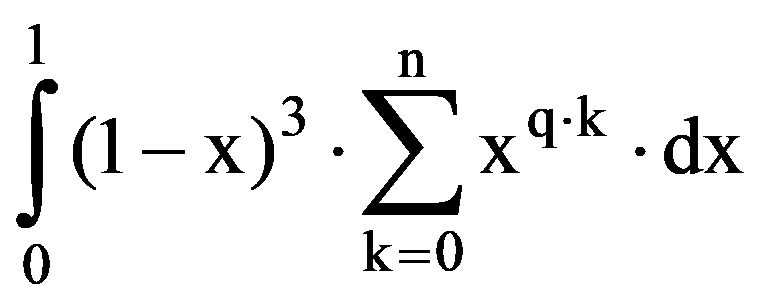
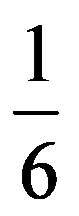
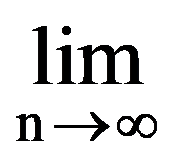
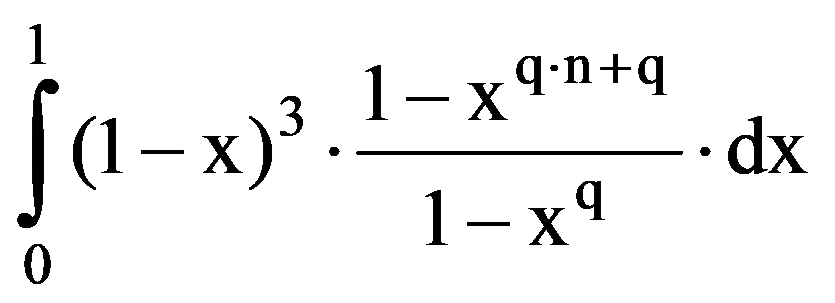
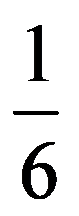
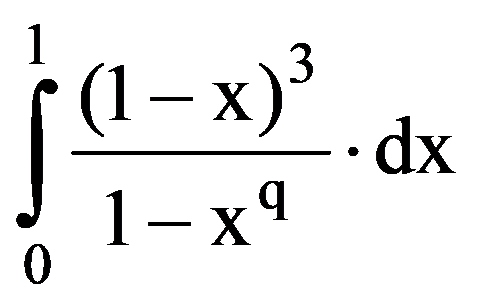
In particular, for q=3:

=

=

=

=

-

ln3+

.

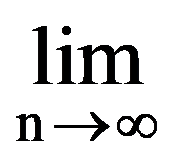
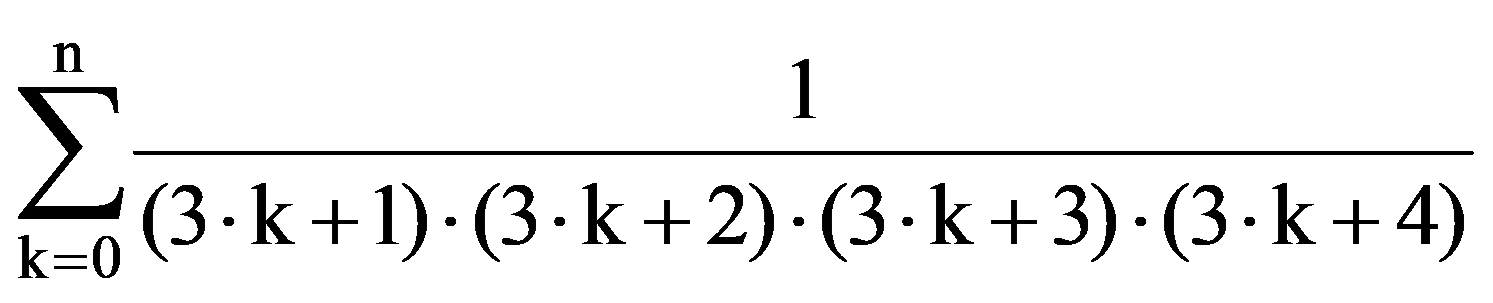
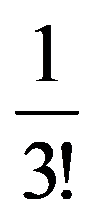
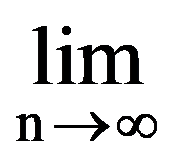
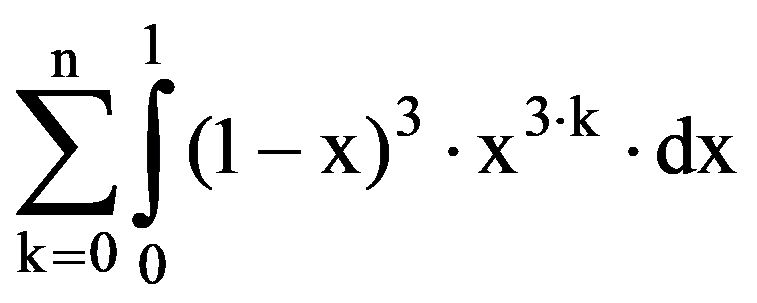
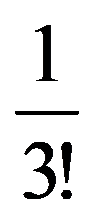
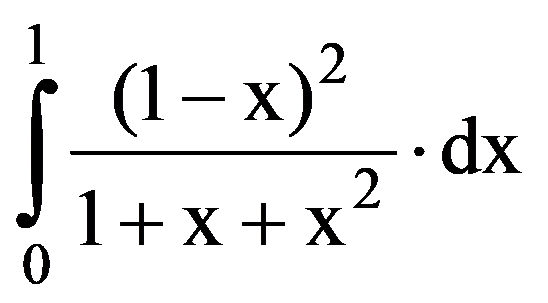
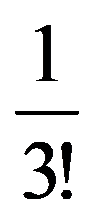
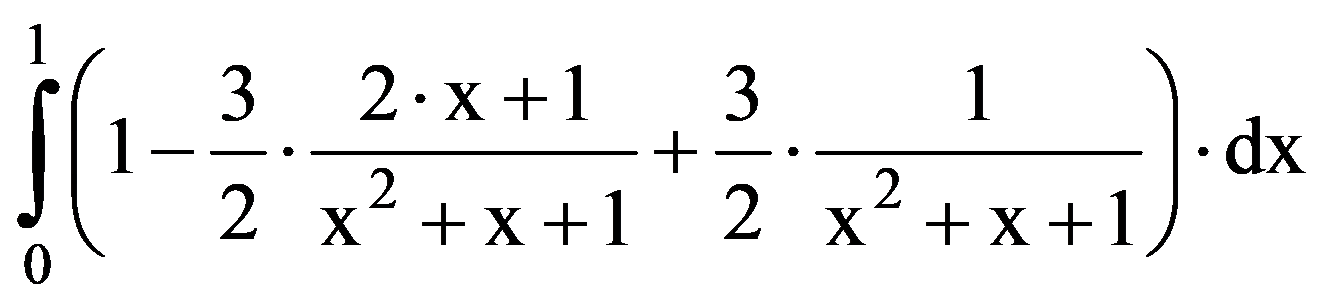
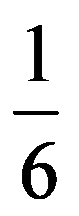
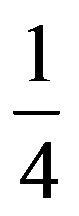
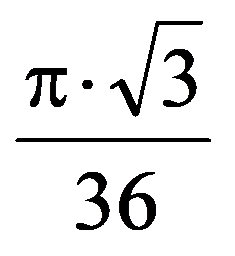
For the calculation of the following limits of sequences we need the following technical result:

Proposition: For every continuous function f : [0,1] (0,+),

=0. (25)

Proof : Indeed, if we denote with I_n=

, then, is checked immediately that the sequence (I_n)_n_N is decreasing and bordered – i.e., for every n N , I_n[0,I₀], where I₀=

. Therefore, the sequence (I_n)_n_N is convergent. We notice also that, for every n N , I_n

, where M=

f(x). Whence, for every n N ,

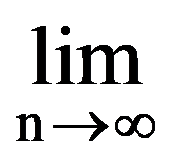
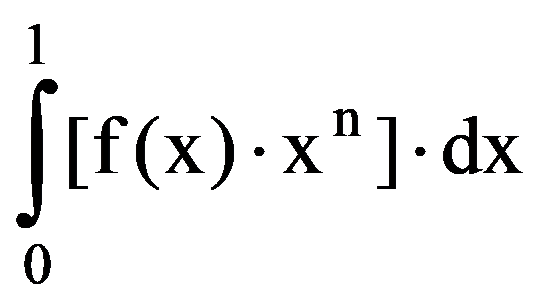
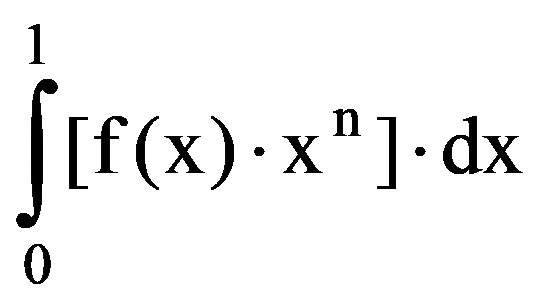
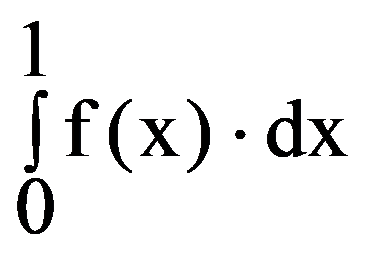
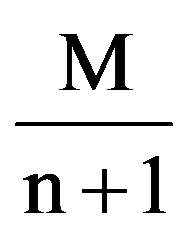
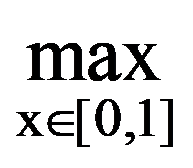
0I_n

. (26)

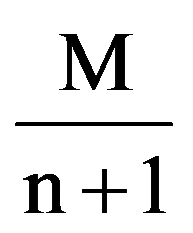
Passing to limit in the inequalities (26), obtain the equality (25).

6.2 The calculation of some primitives and definite integrals

Returning to those presented in the first two paragraphs, observe that, for every p N and every x R \-p-1,-p-2,

,-2,-1, we have the equalities:

I(p,x)=

=

=

=

-

+-

+(-1)^n-1

+(-1)ⁿ

. (27)

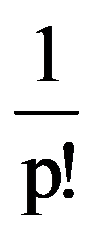
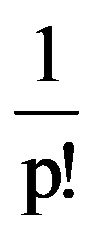
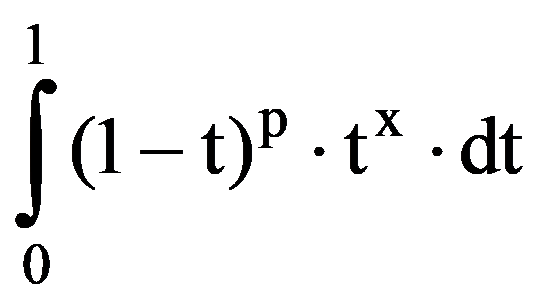
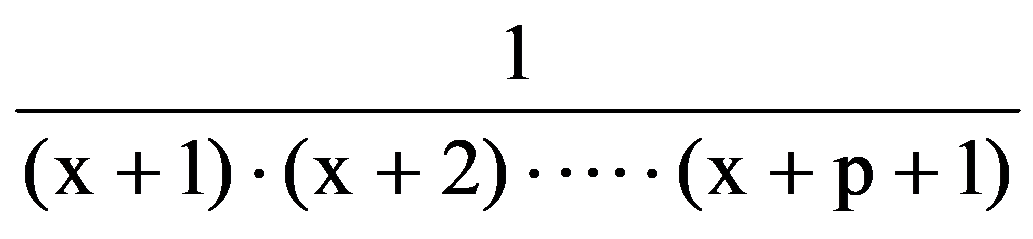
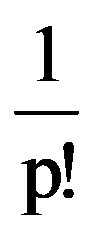
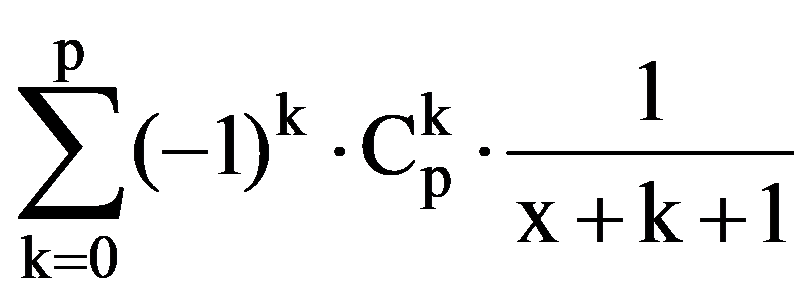
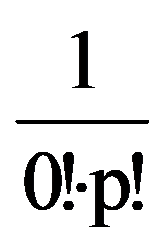
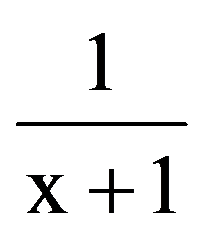
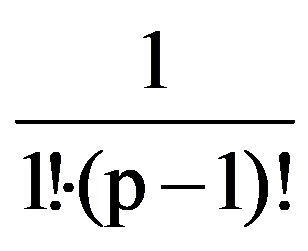
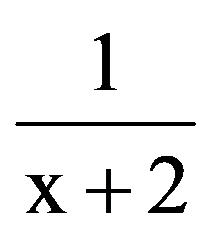
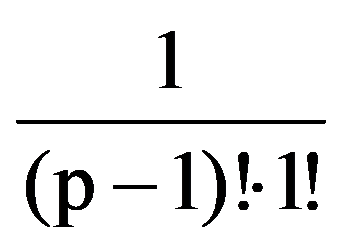
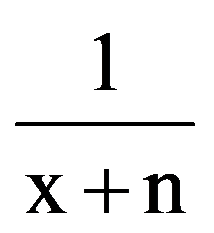
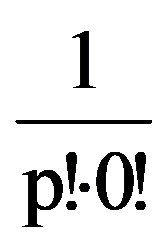
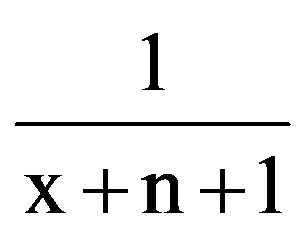
Hence,

=

=

ln(x+k+1)+C; (28)

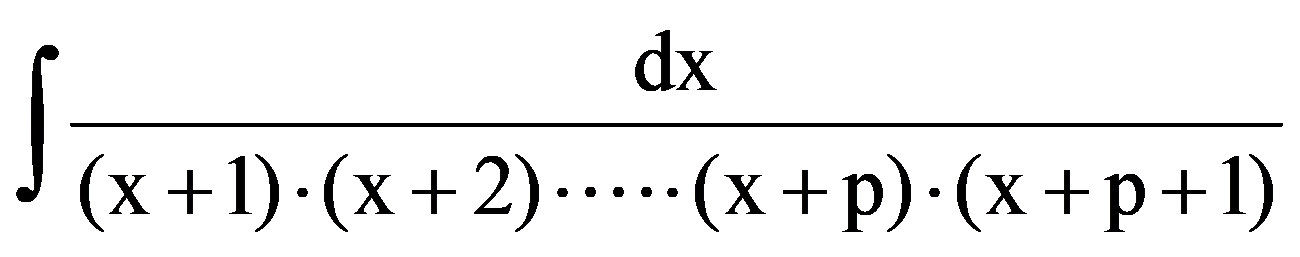
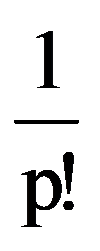
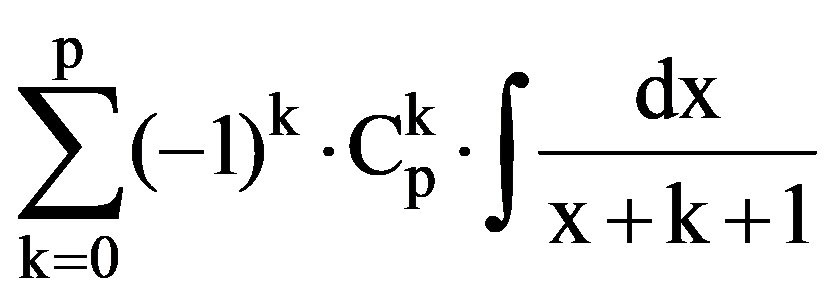
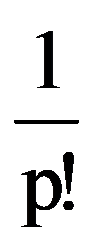
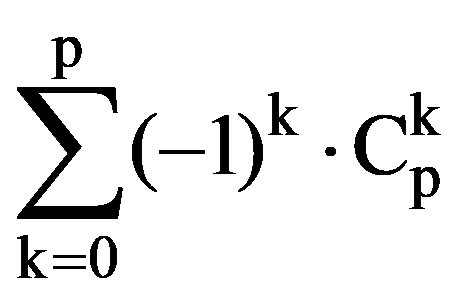
and:

=

=

=

=ln

. (29)

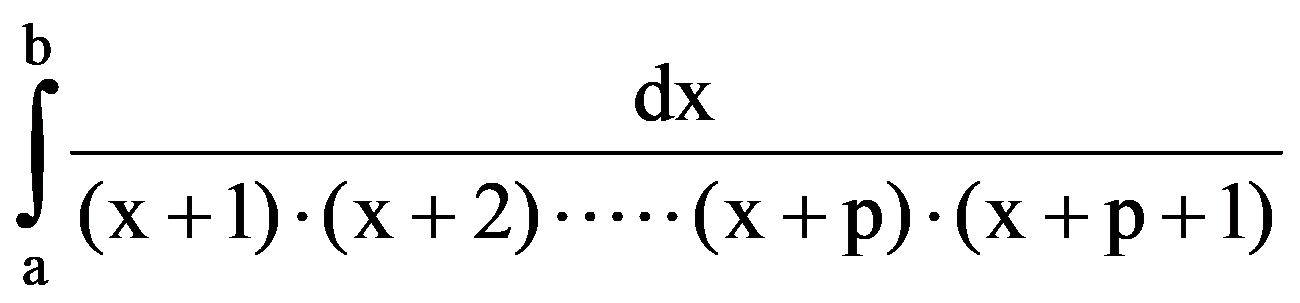
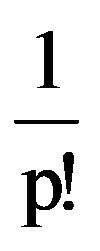
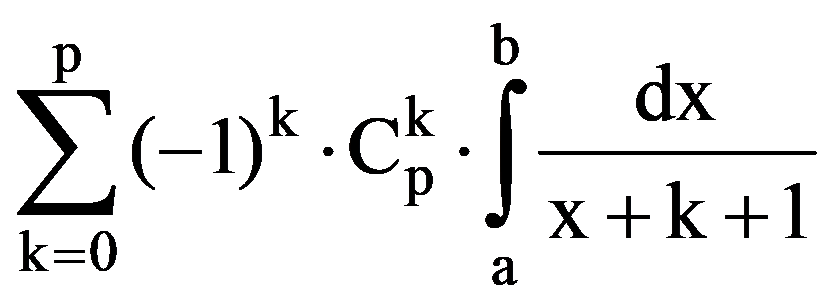
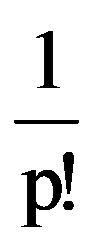
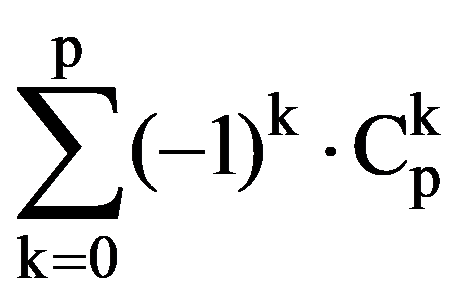
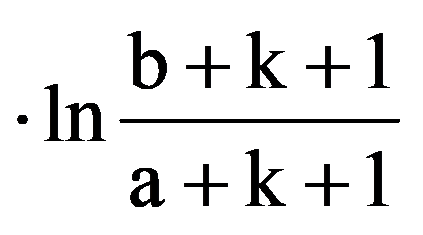
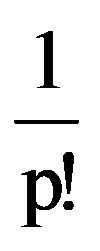
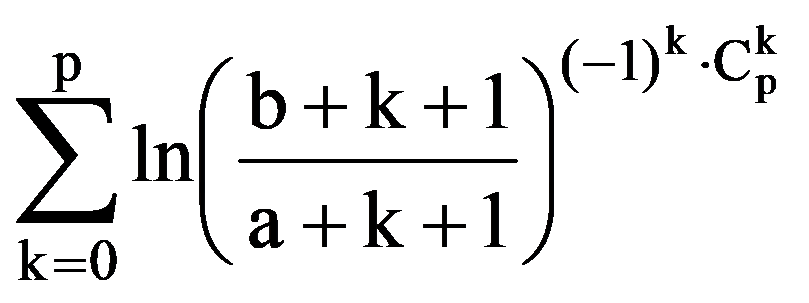
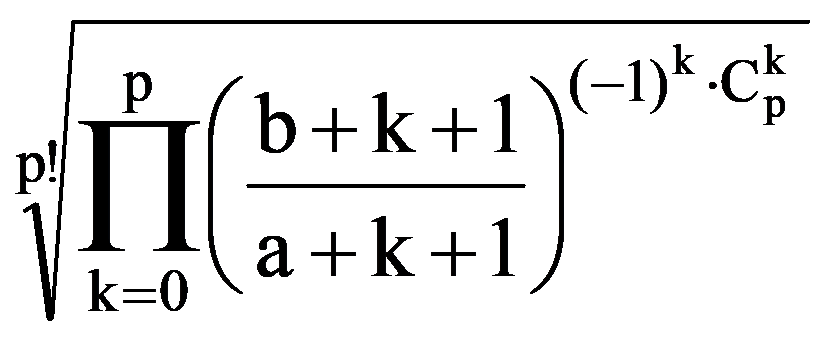
In particular, for p=3:

=

=

ln(x+k+1)+C

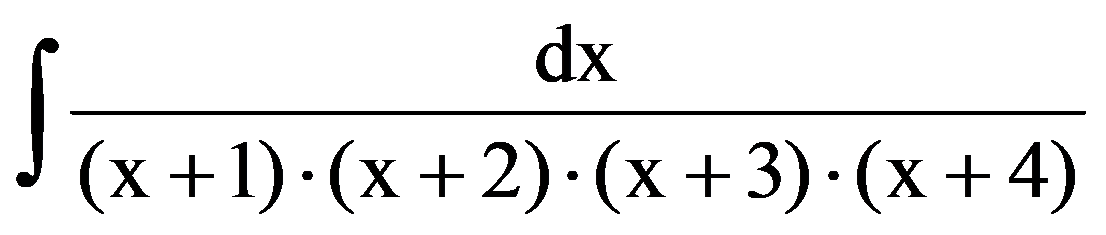
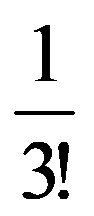
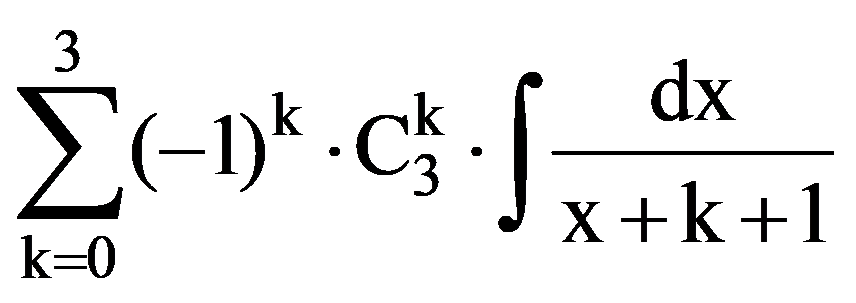
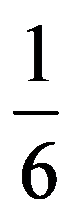
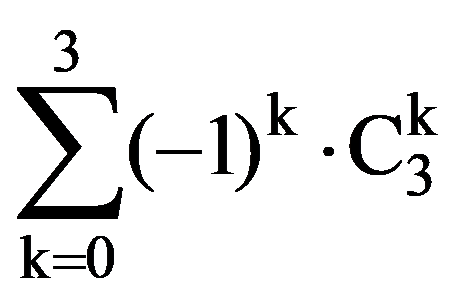
and:

=

=ln

.

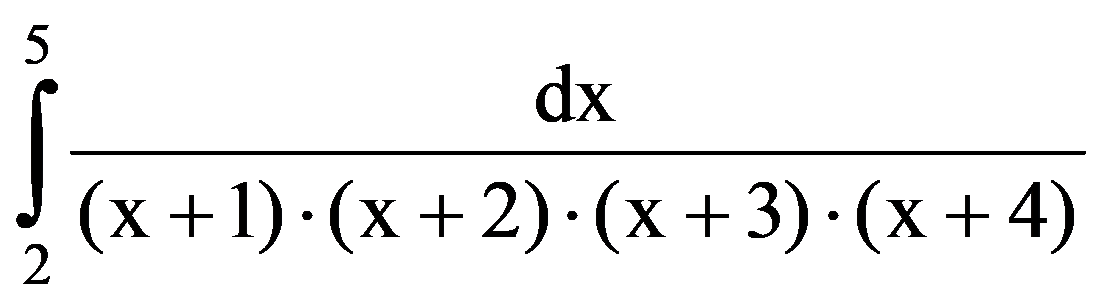
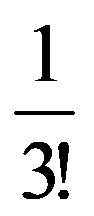
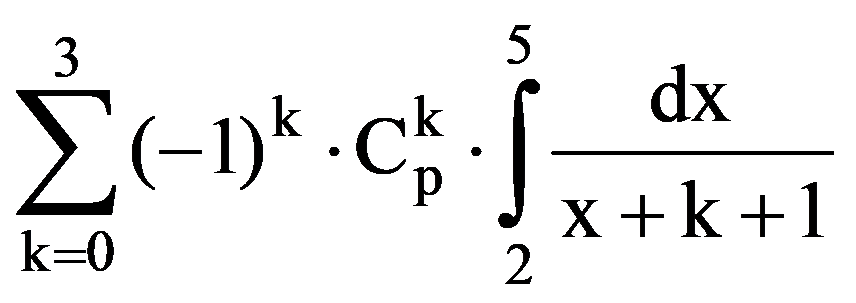
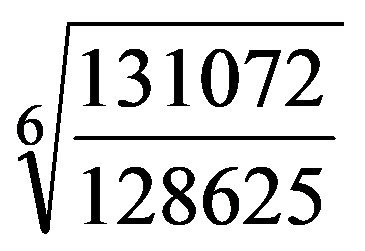
So, the sequences (J(n,n))_n_N above is decreasing and has limits 0.

Conclusions

So from integral I (p, q), which can be calculated in two ways, we can get all identities from (2) to (10). Particularizing these identities obtain the identities (11) and (11). By passing from interval [0,1] at a certain interval [a, b], all identities (2) - (10) can be generalized to yield the identities (13) to (21) identities that then can be customized, achieving equalities (22) - (24), obtaining the identities from (13) to (21), identities that can be particularized, obtaining the equalities (22)-(24). Finally, we presented how you can apply to those shown in the paper in calculating the limits of eight types of convergent sequences, of some primitive and definite integrals. For other examples see Sirețchi (1985).

References

Mocica, Gh. (1988). Probleme de funcţii speciale, (Problems of special functions) Editura Didactică şi Pedagogică, Bucureşti.
http://mathworld.wolfram.com/zetafunction

Copyright information

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

About this article

Publication Date

22 December 2016

Article Doi

https://doi.org/10.15405/epsbs.2016.12.78

eBook ISBN

978-1-80296-017-4

Publisher

Future Academy

Volume

18

Print ISBN (optional)

-

Edition Number

1st Edition

Pages

1-672

Subjects

Teacher, teacher training, teaching skills, teaching techniques, special education, children with special needs

Cite this article as:

Vălcan, T. (2016). An Example of the Training a Methodological Competences in Mathematical Analysis. In V. Chis, & I. Albulescu (Eds.), Education, Reflection, Development - ERD 2016, vol 18. European Proceedings of Social and Behavioural Sciences (pp. 631-639). Future Academy. https://doi.org/10.15405/epsbs.2016.12.78

Copy citation text

An Example of the Training a Methodological Competences in Mathematical Analysis

Abstract

Introduction

Main results

Consequences (1)

Generalizations

Consequences (2)

Applications

Conclusions

References

Copyright information

About this article

Publication Date

Article Doi

eBook ISBN

Publisher

Volume

Print ISBN (optional)

Edition Number

Pages

Subjects

Cite this article as:

We care about your privacy

Manage My Preferences

An Example of the Training a Methodological Competences in Mathematical Analysis

Abstract

Introduction

Main results

Consequences (1)

Generalizations

Consequences (2)

Applications

Conclusions

References

Copyright information

About this article

Publication Date

Article Doi

eBook ISBN

Publisher

Volume

Print ISBN (optional)

Edition Number

Pages

Subjects

Cite this article as:

{title}

We care about your privacy

Manage My Preferences