Learning Abilities and Geometry Achievements

Abstract

Formal geometry is the most problematic subject in middle school and high school math studies. The difficulty stems from the need to understand the language of mathematics in the field of geometry while integrating it with prior knowledge, parallel to the level of the student's mental development. To help students overcome the difficulties in learning geometry a program was developed based on a tool combining use of teaching strategies, through mediation, such as proper use of mathematical and geometric language in particular, including visual marking and identifying memory supports to prior knowledge and using it in the process of finding a solution. This presentation seeks to present findings emerging from research that examined the effect of use of a Learning Strategies Program that combines teaching strategies in solving geometry problems on 10th Grade pupils' achievements, their attitudes towards learning Mathematics in general and Geometry in particular. A Geometry level Van Hiele questionnaire ( as developed by Patkin, 1990 ) and Raven test (2000) mapped the learning abilities of the pupils. The pupils' knowledge regarding solving geometry problems was tested.

Keywords: GeometryStrategiesPupil's attitudesLearning Strategies Program (LSP)Mediation tool

Introduction

Geometry is one of the most important branches of mathematics education, because the aim of the geometry teaching is to provide pupils with the ability of critical thinking, problem solving, and a better understanding of the other subjects in mathematics by making the pupils have a high level of geometric thinking skills (Şahin, 2008).

Difficulties arise from the need to understand mathematical language in the field of geometry, while integrating it with prior knowledge, in parallel to the pupils' level of mental development.

Teaching geometry is a difficult task for teachers. The difficulties require excellent teachers with adequate training and abilities so that thay can carry out the task of mediation between material and learner.

To help pupils overcome learning difficulties in geometry, a program was devised that combines use of teaching strategies.

This program integrates focused teaching strategies acquired by pupils through classroom teaching that give pupils tools to cope with solving other problems. Using this strategy is appropriate for every pupil, does not require repetition or oral memorization by pupils, which have not proven to be tools for solving problems in geometry. Using these strategies enable pupils to develop skills to solve problems at any level. Teaching these strategies will be implemented through mediated teaching in class by teachers in parallel with teaching the contents of the curriculum.

Theoretical Framework

Geometric shapes in general and polygons in particular comprise one of the main topics that accompany pupils from elementary to junior high school. Geometry is perceived by many pupils as the study of formal proof, boring and not understood, and this is because teachers devote lots of time to learning proof, and do not devote any time to developing other important skills, on which geometry is based (Hoffer, 1981).

The important skills for studying geometry according to Hoffer (1981) are: visual skills, verbal skills, sketching skills, scoring, logic skills, practical skills . According to Hoffer a combination of all the aforementioned skills in teaching geometry, will contribute to increasing pupils' interest in the subject and their understanding of learned material. Acquiring these skills is the basis for learning geometry, however this is not enough. There is also a need for children to reach a required level of mental development in order to understand geometry.

Van Hiele's Theory (1959) is the main theory engaging in the development of geometrical thinking. The theory discusses the various stages of mental development of geometry learners. Acquisition of skills is fundamental to the learning of geometry, but it is necessary for pupils to reach a level of mental development required for understanding geometry. Geometry learners' mental development can be hierarchically arranged on five levels. Sarfaty and Patkin (2011) listed the levels of geometric thinking: Recognition , Analysis , Ordering , Deduction, Rigor .

Piaget (1960) and other researchers have emphasized the covert cognitive processes occurring within the learner, meaning the learner's individual development. In contrast, Vygotsky (1978) emphasized social-cultural processes as the source of intrinsic cognitive change. Vygotsky argued that developmental processes and learning processes are not the same. The developmental process follows learning. The latter takes place in the zone of proximal development and the learning process becomes a developmental process (Miller, 2011). According to Vygotsky, what exists within the child as Zone of Proximal Development will appear in the future as actual development.

A strategy of teaching in stages, according to Galperin (1992a, 1992b), serves as a guideline for teachers and not as a collection in a teaching guide that must accompany every individual. He particularly emphasized four unique stages (steps) of the teaching-learning process: (1) orientation, (2) communicated thinking, (3) dialogical thinking and (4) acting mentally. The nucleus of teaching and learning is found in conceptualizing mental process and abilities originating in significant shared activities, presenting children with such activities, giving them cognitive tools and directions to a process that leads to their development. These ideas can help develop a framework in which there is a more profound reference to mutual influences between teaching, learning and development.

Teaching geometry is a difficult task for teachers. Geometry teachers need to develop expertise in the formal part of the subject and its combination with verbal explanations, which have special wording geometry. These difficulties require teachers with high discourse capacity, who are qualified and capable so that they can fulfill the task of mediating the material to the learner in a heterogenous group of learners while using varied tools and skills and develping solution strategies that will constitute a significant and meaningful mediation tool.

Teaching strategies are defined as ways that the teacher takes to accomplish the objectives of the lesson (Schroeder, Scott, Tolson, Huang & Lee, 2007). Learning strategies are a way to improve teaching and learning. In addition, they are a series of cognitive processes that influence information processing in order to provide pupils with tools that will help them learn, solve problems, and complete tasks independently. Strategies of teaching formal geometry are based on the characteristics of the processes which allow for quality teaching-learning-assessment processes as defined in Director General Circulars (2012) in Israel.

Mathematical discourse requires a process of mediating the causality of mathematical phenomena between teacher and pupil (Regev & Shimoni, 2000). Therefore, the discourse is guided by presenting a problem and finding possible ways of solution.

The proposed program is based on Feuerstein's approach (1998). Feuerstein believed the pupil is able to acquire not only knowledge and skills but also new cognitive structures and this realizarion requires an investment of effort and resources. This ability is imparted to pupils through mediated learning in which he or she has direct interaction with the environment through direct exposure. This direct interaction and exposure provides the learner not only knowledge or skill, but also ways of observation, approaches and ways of finding the link between them.

Research Justification

In order to help pupils overcome difficulties in learning geometry, a program was developed, which integrates teaching strategies such as correct use of the geometry language, with visual scoring and finding memory supports for prior knowledge and using it to solving problems in geometry.

This research seeks to examine the influence of Learning Strategies Program (LSP) intervention program on pupils' achievements in geometry and their attitudes towards mathematics and geometry. The article relates to the issue of the contribution of a strategy based program to pupils' achievements in and their attitudes towards geometry and mathematics.

Previous Studies on Similar Programs

Different studies (Hershkovitz, 1992; Kramersky, 1996; Pelach-Borowitz, 2004; Shalev, 2002) have dealt with the link between using teaching strategies and pupils' achievements. Practice strategies based on computers, using drawings in geometry and Van Hiele's levels of thinking model (Idris, 2009; Kutluca, 2013; Patkin, 1994) to solve problems in geometry as well as different strategies used by mathematics teachers in teaching computational geometry, trigonometry (Aydoğdu, 2014). There are those that dealt with different factors and thinks between them and the ability to solve problems in geometry, such as: motivation, feelings, drawing skills (Bailey, Taasoobsshirazi & Carr 2014).

No studies were found that dealt with the construction of models of strategies in teaching geometry which constitutes a mediation discourse between teacher and pupil and their use in high school.

As such, the researcher chose to conduct research whose aim is to examine the influence of a mediated strategic tool in geometry and its use on pupils' achievements in solving problems in geometry and their views with regard to mathematics and geometry in particular.

LSP Program

The Learning Strategies Program (LSP) includes six sessions of approximately 4 hours per session. Each session includes a teaching outline of the tool and employing it while teaching the deductive language of geometry, and at the same time, teaching the "Thinking Persons" tool and instructions of how to use it.

Methodology

In order to check the research question and hypothesis a quantitative research approach and tools were chosen.

Findings

The findings chapter will be divided into four parts. The first part findings from an examination of the starting levels of the three research groups will be presented. The second part will present findings that examined the difference in geometric achievements. The third part will present finding that examined pupils' attitudes to geometry and the fourth part will present findings that examined pupils' beliefs regarding mathematics.

Knowledge and Understanding of Geometry before the LPS intervention

See Full Size >

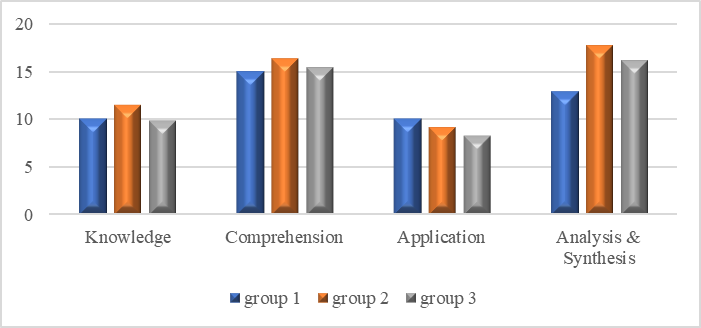
Data analysis was carried out according to van Hiele's levels of thinking. It was found that in three of the four criteria, control group 2 received the highest scores in relation to the other two groups. Differential analysis was carried out on each of the variables, the results showed that there is no significant difference in the achievements at each level (Knowledge, Comprehension, Application), with the exception of Analysis & Synthesis, where a significant difference was found in the level of thinking [F(2.73)=5.191; p=0.0080] between the groups. Bonferroni post hoc test found that group 1 differed from group 2 [M=17.667 (Sd.= 4.7150), M= 13.000 (Sd.= 6.1838) respectively].

See Full Size >

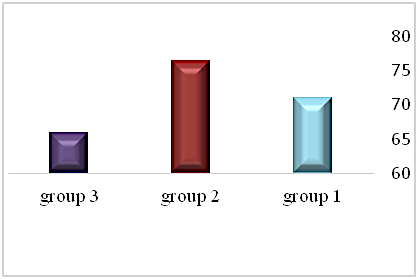
In order to examine differences between the three groups, a one-way ANOVA analysis was carried out between the groups. It was found that there were no significant differences between the groups, however it is possible to say that control group 2 got the highest score (M=76.370 (Sd.=20.040)) in the test and experimental group 3 got the lowest score (M=65.833 (Sd.=23.462)).

See Full Size >

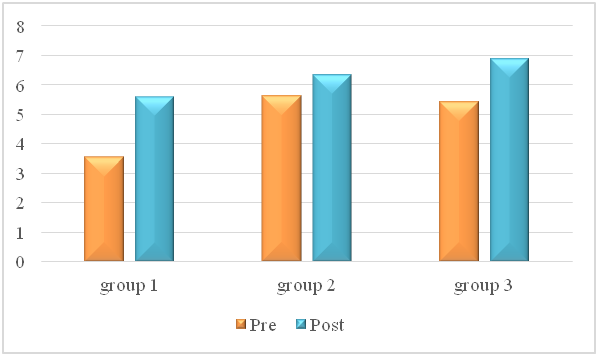
In order to examine differences between the three groups before and after and the interaction between time and group, a two-way ANOVA analysis was carried out between the groups. It was found that there were no significant differences between the groups [F(2.73)=2.033; p=0.138]. The time-group interaction did not yield significance either [F(2.73)=0.548; p=0.580].

It was found there were no differences between the groups before and after the interaction. However, improvements were seen in the mean scores in the experimental group 3.

Differences in achievements in geometry during and after the LSP

See Full Size >

See Full Size >

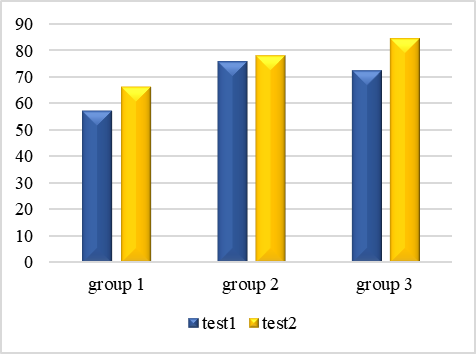
In order to examine differences between the three groups before and after and the interaction between time and group, a two-way ANOVA analysis was carried out between the groups. It was found that there were no significant differences between the times [F(1.73)=2.118; p=0.150]. In contrast, differences were found between groups beyond time points [F(2.73)=3.129; p=0.050], but no interaction was found between time and group [F(2.73)=0.322; p=0.726].

It was found that experimental group 3 received the highest score on average in the test after the program (84.167). Moreover, the average score of experimental group 3 increased the most (12.084) of all groups between the intermediate test and test on completion of the program.

Conclusion

This research examined the effect of the LSP intervention program on pupils' achievements in geometry and their attitudes towards mathematics and geometry. The research hypothesized that group 3 will have the highest achievements in a geometry test after the program. In addition, experimental group 3 would show the greatest improvement between the first and second geometry tests. Moreover, a difference would be found between the groups with regard to problem solving skills and the last assumption was that group 3 would reveal more positive attitudes towards mathematics and geometry.

Using analysis tools it was found that control group 2, whose initial data was highest of the three groups in the Raven test, van Hiele Questionnaire and test to examine their level in geometry. That is to say that is possible to conclude from this that control group 2 had the highest level of geometry prior to introducing the geometry learning.

At the end of teaching geometry and the LSP, according to data analysis, it was found that all three groups had improved their results in the second geometry test in contrast to the first. In addition, it was found that experimental group 3 received the highest average mark of the three groups in the final test (84.167). Moreover, the average mark of group 3 increased the most (12.084) of the three groups between the first test and second test. Adding it to this the finding that improvements were seen in the mean scores in the experimental group 3 at the second van Hiele test. It can be said that it is possible to conclude that the group that underwent the LSP (experimental group 3) on average improved its achievements the most, this despite the fact that in the starting data the control group 2 had the highest average level of knowledge, understanding, analysis and synthesis and as well as in the Raven test and van Hiele Questionnaire. As such, it is possible to say that the first and second research hypotheses were confirmed. Furthermore, it is possible to conclude the same with regard to problem solving skills in geometry. According to data analysis of the intermediate and final tests in geometry it was found that the greatest average improvement was in the experimental group 3 that went through the LSP. As such it is possible to say that hypotheses No. 3 was correct according to data analysis. These findings support the various theories presented in this review, such as Hoffer (1981) who spoke about the combination of skills (visual, verbal, logical etc.) when teaching geometry, will contribute to increasing pupils' interest in the subjects and understanding of learned material, or Galperin's theory (1992b), which argued for the importance of conceptualizing mental processes and abilities whose origins are in meaningful, joint activities, providing cognitive tools and directions as a factor of pupils' development and learning.

With regard to hypothesis No. 4, data analysis showed there was no significant between the groups with regard to capability, intrinsic motivation or self-direction. In addition, there was no difference between the groups in the tests prior to and after conducting the program with regard to beliefs about mathematics, learning mathematics and capability. It is possible that this data emerges for a number of reasons. It is possible that following the relatively short amount of time between conducting the program and carrying out the research constituted a crucial factor in the significance of the results, the process of internalization and learning is a long process, especially when speaking about beliefs and attitudes, for them to be significantly assimilated. This is supported by Vygotsky's (1978) theory that argues that developmental and learning processes are not the same. The developmental process follows the learning process. The learning process takes place in the zone of proximal development area and the learning process becomes a development process (Miller, 2011). Further support can be seen in Galperin's (1992b) theory that conceptualizes internalization action as a transformative process of individuals' external activities to another mental form of the same external activity, and as a consequence to assimilate new knowledge and skills. That is to say that the time factor should also be emphasized in order to examine beliefs and attitudes expresses by children's developmental processes.

In conclusion, the article chose to bring quantitative examination to the research hypotheses, but one must remember that mixed method research was chosen, out of an understanding that variables such as beliefs and attitudes towards mathematics and geometry can be examined more accurately and profoundly in qualitative research, using interviews. In addition, qualitative research methods can glean a greater and more relevant amount of information about pupils' cognitive thinking processes in solving mathematical problems using the 'thinking person' strategy.

References

1. Arievitch, I. M., & Haenen, J. P. (2005). Connecting sociocultural theory and educational practice: Galperin's approach. Educational Psychologist, 40(3), 155-165.
2. Aydoğdu Z. M. (2014). A Research on Geometry Problem Solving Strategies Used by Elementary Mathematics Teacher Candidates. Journal of Educational and Instructional Studies in the World, Volume: 4 Issue: 1 Article: 07
3. Bailey, M. Taasoobshirazi, G. Carr, M. (2014). A Multivariate Model of Achievement in Geometry. Educational Psychology. Vol. 26, No. 3, June 2006, pp. 339–36
4. Feuerstein, R. (1998). Man as a Changing Being: On Mediated Learning Theory. Tel Aviv: Ministry of Defense Publications (In Hebrew).
5. Galperin, P. I. (1992a). The problem of activity in soviet psychology. Journal of Russian and East European Psychology, 30(4), 37–59.
6. Galperin, P.I. (1992b). Stage-by-stage formation as a method of psychological investigation. Journal of Russian and East European Psychology, 30, 4. P. 60-80.
7. Hershkovitz, S. (1992). The Contribution of Schemes for Solving Two-Echelon Word Problems in Math. Thesis for Ph.D., Haifa University, Israel
8. Hoffer, A [1981]. Geometry is More than a Proof. The Mathematics Teacher, 74(1): 11-18.
9. Idris, N. (2009). The impact of using geometer sketchpad on Malaysian Achievement and Van Heile geometric thinking. Journal of Mathematics Education, Vol. 2 No. 2 pp. 94-107.
10. Kramersky, B. (1996). The Development of Mathematical Language in Different Learning Environments. Thesis for Ph.D., Bar Ilan University, Ramat Gan, Israel.
11. Kutluca, T. (2013). The effect of geometry instruction with dynamic geometry software; GeoGebra on Van Hiele geometry understanding levels of pupils. Global Educational Journal of Science and Technology, Vol. 1 (1) pp. 1 – 10.
12. Miller, P. H. (2011). Theories of Developmental Psychology (Fifth Edition), NY: Worth Publishers Chapter 2, 4.
13. Ministry of Education (2012). Director General Circular 9(A), retrieved from: http://cms.education.gov.il/EducationCMS/Applications/Mankal/Templates/HoraotKevaFreeContent.aspx?NRMODE=Published&NRNODEGUID=%7bA3BE1402-899B-461C-8631- EE1E722B0A35%7d&NRORIGINALURL=%2fEducationCMS%2fApplications%2fMankal%2fEtsMedorim%2f3%2f3-1%2fHoraotKeva%2fK-2012-9-1-3-1-43%2ehtm&NRCACHEHINT=NoModifyGuest#3
14. Patkin, D. (1990). The utilization of computers: Its influence on individualized learning, pair versus individualistic learning. On the perception and comprehension of concepts in Euclidean geometry at various cognitive levels within high school pupils. Doctoal dissertation, Tel-Aviv, Israel: Tel-Aviv University. [Hebrew]
15. Patkin, D. (1994). Influence of using computers on levels of geometric thinking. ALEH- Mathematics Teaching Journal, 15, pp. 29 – 36 (In Hebrew).
16. Pelach-Borowitz, D. (2004). Identifying Strategies and Good Teaching Skills in the Mathematics Learning Unit in the Sixth Grade. MA Thesis, Tel-Aviv University, Israel.
17. Piaget, J., Inhelder, B. & Szeminska, A. (1960). The Child's Conception of Geometry. New York: Harper Torchbooks
18. Pinchevsky, R. (2001). Influence of Mathematics Teachers' In-Service Courses on Teachers and pupils' beliefs. Ramat Gan: Bar Ilan University, School of Education (In Hebrew)
19. Raven, J. (2000) "The Raven's progressive matrices: change and stability over culture and time." Cognitive psychology 41.1: 1-48.
20. Regev, H. Shimoni, S. (2000). Speaking Mathematics – What for? Why? How? ALEH- Mathematics Teaching Journal, 25, pp. 77 – 89 (In Hebrew).
21. Şahin, O. (2008). In-& pre-service elementary school teachers? Van Hiele reasoning stages. Master Thesis. Kocatepe University, Institute of Social Sciences, Afyo
22. Sarfaty, Y. Patkin, D. (2011). The Effect of Solid Geometry Activities of Pre-service Elementary School Mathematics Teachers on Concepts Understanding and Mastery of Geometric Thinking Levels. Hachinuch Usvivato, 33 pp. 177 – 193 (In Hebrew)
23. Schroeder, C. M., Scott, T. P., Tolson, H., Huang, T-Y. & Lee, Y-H. (2007). A meta-analysis of national research: Effects of teaching strategies on pupil achievement in science in the United States. Journal of Research in Science Teaching, 44(10), 1436-1460.
24. Shalev, P. (2002). Teachers' Perceptions of the Use by Pupils with Learning Disabilities of Learning Strategies. MA Thesis, Tel-Aviv University, Israel.
25. Van Hiele, P.M.,La Pensee de I'Enfant et La Geometrie, Bulletin de I'Association des Professeurs de Mathematiques de I'Enseignement Public 198, 199-205 (1959)
26. Vygotsky, L. S. (1978). Mind in Society: The Development of Higher Psychological Processes. Cambridge, MA: Harvard University Press.