Abstract
A key mathematics competence included in curriculum of European countries is “Applying mathematics in real-life contexts”. The present paper points out the particularities of the transition from the pre-university education to the academic environment, by offering reflections about high-school graduates’ competence on using mathematical knowledge in real-life contexts. The subjects involved in this study were candidates for the Primary and Preschool Education Pedagogy specialization of the Faculty of Psychology and Science of Education, Babeș-Bolyai University, Cluj-Napoca. The data reported is derived from a comparative analysis of the real-life problems’ contents and solutions registered in the last three years’ written examinations that verified participants’ knowledge in Arithmetic. The scores obtained for the proposed problems shows that around 10% of high-school graduates are not capable by a mathematical approach of a real-life problem. Around 57% of them can solve at most a half of problem, that show a partially understanding of the problem’s context, achievement of intermediary results but the impossibility of their correlation in order to solve the problem. A percent of 17% of candidates solved the problem but we have to consider that a part of them are already preschool or primary school teachers who want to complete their studies.
Keywords: High-school graduatesPrimary and Preschool Education Pedagogy specializationadmissionBabeș-Bolyai Universitykey mathematic competencereal-life problems
Introduction
”In all European countries, the mathematics curriculum has been revised during the last decade and, in the vast majority of countries, important updates have been introduced since 2007” according to document
According to the previous document in these new mathematics curriculum and/or other mathematics steering documents are included next key mathematical competences:
Mastering basic skills and procedures;
Understanding mathematical concepts and principles;
Applying mathematics in real-life contexts;
Communicating about mathematics;
Reasoning mathematically.
Magdaş and Rǎduţ (2014) have analyzed the level of mathematical knowledge of high-school graduates in Romania. Some worrying conclusions of that research are that “over 10% of the high-school graduates cannot do an addition or subtraction right and around 17% have the same problem with multiplication, while 20% have troubles with the division”. As a continuation of that study in this article we study the level reached by the high-school graduates on competence “Applying mathematics in real-life contexts”.
Key mathematics competence “Applying mathematics in real-life contexts”
One of the key mathematics competences included in curriculum is therefore “Applying mathematics in real-life contexts”. Analyzing mathematics curriculum of 32 countries across Europe, in all of them curricula gives general reference about it. Beside the general reference in 4 countries curriculum includes also specific assessment recommendations, in 3 countries curriculum includes also specific teaching methods, and curriculum of 8 countries includes both specific teaching methods and assessment recommended, Romania being among them (based on figure 1.7 - EACEA P9 Eurydice, 2011).
In 2009 through Romanian preschool curricula were introduced the integrated activities. Through Ministry of Education, Research, Youth and Sports of Romania
At international comparative assessments of students achievement in mathematics and science TIMSS (
Magdaş and Dulamă (2014) consider that “mathematics learning should start from the real life/ environment contexts, within there are identified mathematical concepts (interdisciplinary approach), their acquisition being ensured by an intradisciplinary approach”. The fixation of Mathematical concepts it is made by applying them in Mathematics (intradisciplinary extensions) and in real life contexts (interdisciplinary contexts). Thus “Mathematics feed itself from entirely knowing and affect it entirely” (Marcus S., 1987).
Research description
For our research we considered candidates for the Primary and Preschool Education Pedagogy specialization (PPEP) of the Faculty of Psychology and Science of Education, Babeș-Bolyai University, Cluj-Napoca. All candidates were high-school graduates, having the Baccalaureate Exam promoted. Even if a part of the candidates did not have to take a math exam to the Baccalaureate Exam, they all have passed the national testing for the 8th grade and studied math in at least 10 school years.
Data are collected from the 2013, 2014 and 2015’s Admission Exam, with a total of 889 subjects of which 248 in 2013, 338 in 2014 and 303 in 2015. Subjects and the content being the writing exam to verify their arithmetic knowledge. The given subject for the admission at the PPEP has a mathematics subcomponent. One of the subject proposed is a real-life problem that can be solve by using basic arithmetic operations. For solving this problem, there are only required the knowledge of a mediocre primary school student. Performing some simple mathematical operations (addition, subtraction, multiplication and division) are only partially stages of solving problem. The essence is the understanding of the problem’s context, the identification of intermediary stages and the ability to correlate the partial results with the problem’s requirement.
Proposed problems and their analysis
Next we present the problems for the admission to the Primary and Preschool Education Pedagogy specialization in 2013, 2014 and 2015. Also we make few didactical considerations regarding the thinking way of solving for each problem along with their solution. Each problem has been denoted with 1 point out of a total of 3 points. For making an easier interpretation of results we extend the score at 10 points. The correction scale was elaborated considering that calculation will be noted, without regard to the formulation of questions, if the results are explained correctly.
P1. (2013) In an orchard are 5000 of fruit trees seated in rows of 20 trees. First 148 rows were planted apple trees, the following 59 rows are planted with pear trees, and the rest were planted with quince trees. Find out how many quince trees have been planted and on how many rows.
Problem soving analysis.
1st Method. The solving it is made inductively as follows:
Because it is known the number of fruit trees and the number of rows then can be find:
How many rows of fruit trees are in the orchard? 5000:20 = 250 (rows) (2 pt.)
Because it is known the number of rows planted with apple trees and pear trees then can be find:
How many rows of apple trees and pear trees are together? 148 + 59 = 207 (rows) (2 pt.)
Now can be given the answers at the problem’ questions:
How many rows of quince trees are in the orchard? 250 – 207 = 43 (rows) (3 pt.)
How many quince trees are in the orchard? 43×20 = 860 (quince trees) (3 pt.)
2nd Method. The solving it is made deductively as follows:
The number of quince trees can be find as difference between the total number of trees and the number of apple trees and pear trees. Thus it is find first:
How many apple trees are in the orchard? 148×20 = 2960 (apple trees) (2 pt.)
How many pear trees are in the orchard? 59×20 = 1180 (pear trees) (2 pt.)
then
How many quince trees are in the orchard? 5000 – 2960 – 1180 = 860 (quince trees) (3 pt.)
By knowing the number of quince trees can be find:
How many rows of quince trees are in the orchard? 860:20 = 43 (rows) (3 pt.)
We notice that first 4 points correspond to preliminary calculations, while the last 6 points to understanding the problem context.
P2. (2014) At a social centre were brought 880 kg of sugar, 690 l of oil and 470 kg of pasta. They were wrapped in order to be given to the needy in packages containing each: 4 kg of sugar, 3 l of oil and 2 kg of pasta. What is the maximum number of packages that can be made and what quantity of each product has remained afterwards?
Problem soving analysis. The solving it is made inductively starting from what it is given. Because it is know the sugar, oil and pasta quantities then can be find:
For how many packages is there enough sugar? 880:4 = 220 (packages) (2 pt.)
For how many packages is there enough oil? 690 :3 = 230 (packages) (2 pt.)
For how many packages are there enough pasta? 470:2 = 235 (packages) (2 pt.)
In this stage the preliminary calculations denoted by 6 points are done. Now the answer at first question can be given. The answer depends of the understanding of the context of the problem. It is necessary to identify that the highest number of packages corespond to the lowest value found previously.
Which is the maximum number of packages that can be made? 220 (packages) (1 pt.)
Finding out the total number of packages, even if was marked with 1 point, was the key without which the last 3 points could not be received.
Reasoning is quite simple to find out quantities remained, these are the difference between the amount of used and unsed packages. Such the remained amounts are:
0 kg of sugar (1 pt.)
10 packages × 3 l of oil = 30 l of oil or 690 – 220 × 3 = 30 l of oil (1 pt.)
packages × 2 kg pasta = 30 kg pasta or 470 – 220 × 2 = 30 kg pasta (1 pt.)
P3. (2015) For a raffle sell tickets at a price of 5 lei each ticket. By lottery are given following prizes: a first prize consisting of a schoolbag in amount of 129 lei, three second prizes consisting of a pencil box in amount of 49 lei each and five third prizes consisting of a pen in amount of 25 lei each. What gain is obtained from the sale of 100 tickets? How many tickets should be sold for a gain of 199 lei?
Problem soving analysis. Unlike the first two questions that could partially solve without a fully understand of the problems, here solving involves from the beginning at least a partial understanding of the requirement. Problem solving is deductively starting from the requirement. The gain from the sale of 100 tickets is the difference between the amount received from the sale of tickets and the cost of prizes. Thus it find:
How many lei earns from the sell of 100 tickets? 100 × 5 = 500 (lei) (2 pt.)
- How many lei cost all prizes ? 129 + 3 × 49 + 5 × 25 = 401 (lei) (3 pt.)
A problem can occur in finding prizes’ cost. Due to appearance in the text of numerical values (first prize, second prize, third prize) that are only information necessary for understanding the context, these may confuse solver who doesn’t knows how and where to use them. We can say therefore that context misunderstanding leads to getting a maximum 2 points of total. To find out the earnings, solver must know the significance of gain as the difference between the amount received and spent.
What gain is obtained from the sale of 100 tickets? 500 – 401 = 99 (lei) (2 pt.)
For answering at second question:
How many tickets should be sold for a gain of 199 lei?
solver must correlate previous data and new requirements of the problem. Now he has to observe the gain it is given and must find out the number of tickets, which is vice versa than first situation. Solving requires greater analysis and structured mathematical knowledge, but can be done in three ways.
1st Method. The earn must increase with 100 lei (toward the earnings of the 100 tickets), so it must be sell in adition 100 : 5 = 20 tickets. Thus are necessary 100 + 20 = 120 (tickets)
2nd Method. (401 + 199): 5 = 600 : 5 = 120 (tickets)
3rd Method. Using the equation 5x – 401= 199, we have 5 x = 600, thus x = 120 (tickets) (3 pt.)
A typical mistake we noticed it in the last stage of solving the problem is to apply ”Rule of theree” as follows:
100 tickets … 99 lei
x tickets … 199 lei
from where in a wrong way is obtained x = 100 · 199: 99 = 201.01 tickets
Results and discussions
The histogram of the candidates’ scores for each problem is presented in figure
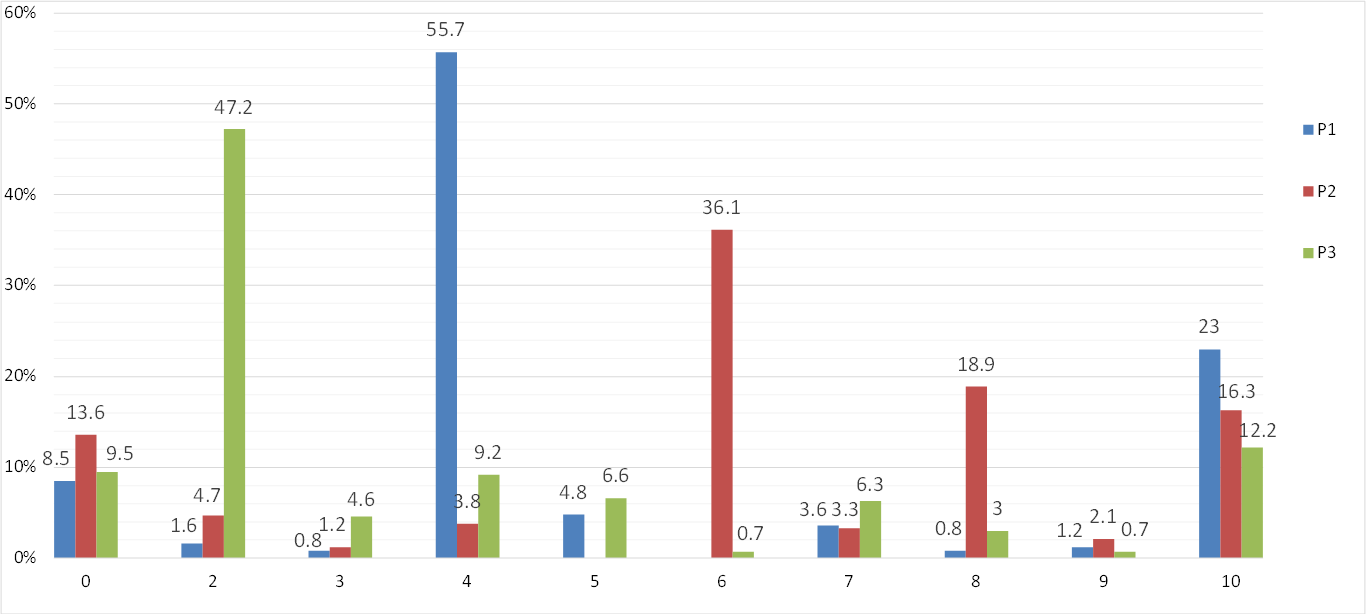
For all problems are noticed a group of scores around values: 0 points, an intermediate value corresponding to the largest number of subjects and at the maximum score. An exception are noticed at P2 where are two thresholds of intermediate scores at 6 points and 8 points.
Modal values are 4 points for P1, 6 points for P2, and 2 points for P3. P1 modal value corresponds for solving correctly intermediate calculations without which the solving can not be continued, which is achieved by over 55% of subjects. At P2 the two thresholds scores correspond to intermediate calculations. We also noticed that the first threshold was passed by over 36% of subjects, and the second still nearly 19%. A different situation is at P3 where the modal score of 2 points corresponds to only a portion of the intermediate computations.
We found that P1 has been solved entirely by most candidates almost a quarter, also having the fewest candidates who received 0 points.
P2 had the highest percentage of subjects who received 0 points (almost 14%), a surprising result because obtaining 6 points consist of three very simple divisions.
At P3 even if the number of subjects who achieved 0 points is less than P2, nearly 10%, however this percentage should be add with the number of subjects who get 2 points because all of these misunderstand the problem’s context. Thus we can say that nearly 57% of subjects cannot identify the subproblems. 37 candidates (12.2%) have fully solved the problem of which 10 of them (27.02%) have solved the problem by using 1st method, 19 (51.35%) by using 2nd method, and 8 of them (21.62%) by using 3rd method.
Analyzing cumulative frequencies scores for all three problems (figure
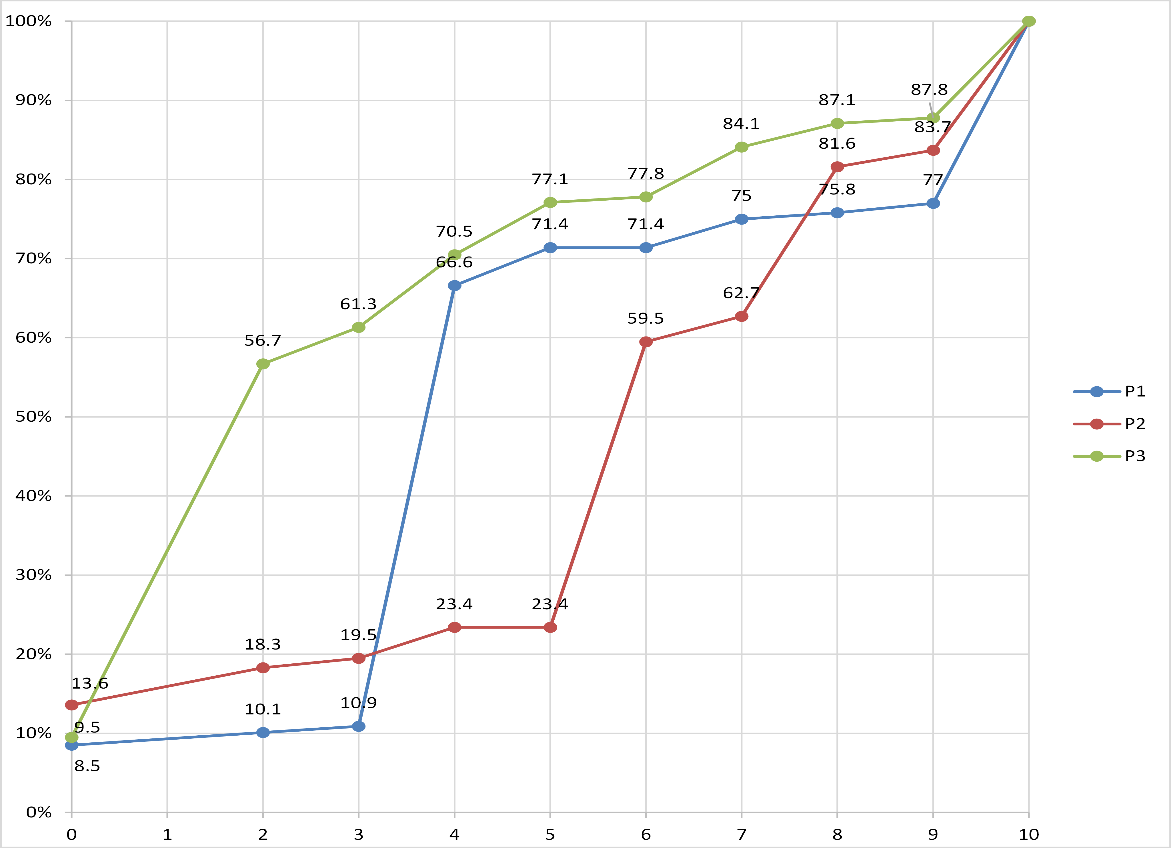
In average 28.36% got up to 2 points solves only a small part of the problem. Maximum 5 points were achieved by 71%, respectively 77% of the candidates at P1 and P3, respectively. At P2 situation is better less than 24% of candidates having scores up to 5 points. In average 57.3% of candidates received at most 5 points.
The average scores for each problem presented in Table
We notice as the highest score was obtained at P2 where intermediate computations up to 6 points were easy to make. It appears that P3 was the most difficult problem for the candidates.
Conclusions
Along with the reintroduction of the admission exams in the Colleges from Romania, we have the possibility to check the level of mathematical knowledge of the high-school graduates in other way than by the Baccalaureate exam. The admission to the PEPP specialization give us the possibility to check the basic arithmetical knowledge of the students, which in most cases have studied math in school on a second plan. Even if the sample is not a representative one, we believe that it can show the the candidates’ capacity to solve real-life problems. The scores obtained for the proposed problems shows that around 10% of high-school graduates are not capable by an mathematical approach of a real-life problem. Over 28% of them barely manage to start solving the problem. This data show that almost 39% of high-school graduates can at most start problem’s solving that means a misunderstanding of the problem’s context. Around 57% of high-school graduates can solve at most a half of problem, that show a partially understanding of the problem’s context, achievement of intermediary results but the impossibility of their correlation in order to solve the problem. A percent of 17% of graduates solved the problem but we have to consider that a part of candidates are already preschool or primary school teachers who want to complete their studies.
Considering the results obtained by this study, we believe that Romania do not fit yet in the EU’s request (Strategic Framework for European Cooperation in Education and Training ('ET 2020'), Council Conclusions of 12 May 2009 that, by the end of 2020, less than 15% of the kids under 15 years old to have insufficient skills at math. And this is especially because there still are children which abandon school, or who do not wish to pursue a college and which have not been included at all in this study.
Since 2020 refers at students who are now in Primary School for which the new curriculum provide interdisciplinary approaches of Mathematics this fact favors the exercise of applying mathematics in real-life situations. On the other hand paradoxically precisely contextualization can be detrimental for managing mathematics algorithms, and so this integration must be done carefully so as to be respected the logic of Mathematics Science and also of Didactics of Mathematics.
References
- Council of the European Union (2009). Strategic Framework for European Cooperation in Education and Training ('ET 2020'), Council Conclusions of 12 May 2009, OJL 119, http://eur-lex.europa.eu/legal-content/EN/ALL/?uri=CELEX:52009XG0528(01) [May, 2016]
- Dulamǎ, E.M. & Magdaş, I. (2014). Analysis the Competences and Contents of “Mathematics and Environmental Exploration” Subject Syllabus for Preparatory Grade, Acta Didactica Napocensia, vol 7. Nr. 2, 11-24.
- Education, Audiovisual and Culture Executive Agency (EACEA P9 Eurydice) (2011). Mathematics in Education in Europe: Common Challenges and National Policies, Brussels, http://eacea.ec.europa.eu/education/eurydice/documents/thematic_reports/132EN.pdf [May 2016].
- Marcus, S., (1987). Șocul matematicii, Ed. Albatros, București.
- Magdaş, I. & Rǎduţ-Taciu, R. (2014). The Analysis of the Results Obtained by the Candidates for the 2014’s Admision, Specialization: “Primary and Preschool Education Pedagogy”, the Mathematical Component, Acta Didactica Napocensia, vol. 7 nr. 3, 11-20.
- Ministry of Education, Research, Youth and Sports of Romania (2012). Framework Plan for the Primary Education. Preparatory Grade, First and Second Grades, Order no. 3654/29.03.2012, http://oldsite.edu.ro/index.php/articles/16945 [May 2016].
- Mullis. I. & Martin, M. (2013). TIMSS 2015, Assessment Frameworks, International Association for the TIMSS&PIRLS International Study Center, Lynch School of Education, Boston College, International Association for the Evaluation of Educational Achievement (IEA), http://timssandpirls.bc.edu/timss2015/downloads/T15_Frameworks_Full_Book.pdf [May 2016]
- TIMSS&PIRLS International Study Center, Lynch School of Education, Boston College, http://timssandpirls.bc.edu [May 2016]
Copyright information

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
About this article
Publication Date
22 December 2016
Article Doi
eBook ISBN
978-1-80296-017-4
Publisher
Future Academy
Volume
18
Print ISBN (optional)
-
Edition Number
1st Edition
Pages
1-672
Subjects
Teacher, teacher training, teaching skills, teaching techniques, special education, children with special needs
Cite this article as:
Magdaș, I., & Glava, A. (2016). Analyzing the High-School Graduates’ Competence on Applying Mathematics in Real-Life Contexts. In V. Chis, & I. Albulescu (Eds.), Education, Reflection, Development - ERD 2016, vol 18. European Proceedings of Social and Behavioural Sciences (pp. 202-209). Future Academy. https://doi.org/10.15405/epsbs.2016.12.27

