Integral Formation and Metacognition from the Mathematical Dimension

Abstract

This article presents the results of an investigation to establish the relationship between metacognition and the construction of mathematical knowledge when this is carried out in a mathematics classroom of an engineering area. In order to identify the elements that enable implementation of cognitive and metacognitive strategies that will to lead the continuous improvement of student academic performance from the mathematics dimension. The methodology used was the construction of a conceptual cartography with metacognition as the central theme, and through its eight axes of analysis, the documentary sources were the epistemological cognitive and didactic areas. The framework was the socioformative approach, the integral formation guided by the educational model of the educational institution: the Instituto Politecnico Nacional, within the area of engineering. The mathematics subjects are taught in the first four semesters of the academic programme, so students are aged in the range of 19–22 years. Results: a direct relationship was evident between the elements of a metacognitive process and mathematics through problem solving. The work allows us to conclude the importance of articulating that the cognitive dimension (in this case in the field of mathematics), metacognitive dimension and emotional dimension developed by solving problems could promote specific and essential competences of graduate profile of an engineer.

Keywords: Conceptual cartography of metacognitionintegral formationmetacognition and mathematicsproblem solving

Introduction

This document approaches a way of confronting the fundamental changes in the Educational Model

of the Instituto Politecnico Nacional. The central change is that the process of teaching-learning now

focuses on the learning of the student, to promote an integral formation from the complexity and

articulating the four pillars of education: to be able to be, be able to live together, to learn to know and

know-how (IPN, 2004). Integral formation has been the focus of most educational institutions, placing

the student’s learning at the centre of the formative process. The Social formation of Sergio Tobon

(2001) is a formative approach that is defined as a perspective that is orientated towards the integral

formation, from the boarding problems of the social, cultural or academic context of the student, in a

frame of collaborative work, considering the ethical project of life of each one of the actors of the

process of teaching and learning. It promotes the management and co-creation of knowledge and

metacognition as a way for permanent and constant improvement, taking as a base the technologies of

information and communication (Tobon et. al., 2015). This has led to changes in the depth and forms of

the teaching activity in order to achieve the objective.

On the other hand, it is thought that a problem is something that confuses the human mind,

challenges it and obscures beliefs (Sengul & Katranci, 2012). With this as a base, it can be said that in

the process of resolution of problems the aptitude to create, to invent, to reason and to analyse different

situations is stimulated when the students solve them (Perez & Ramirez, 2011). Likewise, Schoenfeld

(1987) made studies that related the mental performances that are important for the resolution of

mathematical problems, dividing them into three categories: the management of the information related

with the control of the cognitive process, the actions that control it, and the processes of auto-regulation

related with the beliefs and attitudes; all of these were identified with a metacognitive process (Perez &

Ramirez, 2011).

This paper’s research used the cognitive dimension as a referential axis, in this case this dimension

was mathematics. Within this discipline the subjects considered were differential and integral calculus

studied in the first semester and vectorial calculus in the second semester. These subjects had a high

failure index in our institution. The students had an age range between 19 and 22 years and some did

not have the necessary cognitive background to develop new knowledge.

The research focused on answering the question: how is it possible to contribute to the integral

formation through the mathematics given in the classroom of the future engineer, promoting improved

academic performance in the subjects of the curricula (beginning with mathematics), with social

commitment in a process of constant improvement to confront the resolution of problems of any

context?

Method

2.1.Type of research

The research was placed in the higher level in the area of basic sciences formation. The research was

qualitative and was carried out by means of documentary analysis concerning the concept of metacognition. The bibliographical and hemerographical sources were situated inside the cognitive

dimension (mathematical), the didactic dimension for the discipline (educative mathematics) and the

socioformative dimension. The research presents a method for the integral formation of an engineer,

due to the fact that it offers a methodology for the classroom from which the competences of the

graduate profile are promoted. These include: autonomous learning, learn to learn, collaborative work,

simultaneously promoting the values of responsibility, solidarity, honesty and social compromise

(Rodriguez, Aniceto & Rojo, 2013).

2.2.Strategy of research

The methodology of conceptual cartography was used for the analysis, presentation and organisation

of the information (Tobon, 2004; Tobon, 2012; Tobon et. al., 2015). This consists of following at least

eight axes of analysis orientated by questions concerning a central topic. With this methodology, any

topic, concept, methodology and even a theory can be studied in depth, systematising the existing

information, constructing the aspects lacking detail on the basis of the information that already exists,

to understand it and to communicate it to the academic community. Figure 1 shows the eight key axes

of the conceptual cartography.

See Full Size >

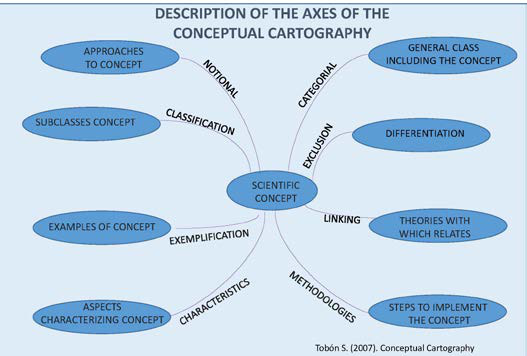
For example, on the axis of notional analysis, the guiding question can be: what is the etymology of

the concept of metacognition? What is its historical development? What is the current definition? Or on

the entailment axes: how is socioformation related to metacognition? How is educational mathematics

related to metacognition and problem-solving?

2.3.Phases of the research

Phase 1. Search of primary and secondary sources. The documentary research was approached

following the key words: integral formation and mathematics, socioformation and metacognition,

metacognition, metacognition and mathematics, resolution of mathematical problems and

metacognition. Searches based on these terms were undertaken in databases such as EBSCO,

Journalseek, and SCOPUS and across Google, Google Scholar and the databases that manage the

Instituto Politécnico Nacional (IPN).

Phase 2. The analysis of documents was undertaken, establishing relationships between integral

formation and socioformation, and metacognition and the metacognitive process with the resolution of

mathematical problems and, the resolution of problems and socioformation.

Phase 3. The conceptual cartography was constructed following eight axes of analysis concerning

metacognition, under the frame of integral formation from the mathematical dimension and

contribution to the formation of an engineer.

Results

Some relevant aspects selected from the results of the conceptual cartography are presented below.

3.1. Metacognition

Metacognition is the knowledge of a reflective and conscious way, about what is known of the

learning process for his regulation and control. Knowledge refers to those elements or variables, and

the cognitive processes that intervene in the acquisition of knowledge are memorisation, attention,

perception, comprehension, and communication; planning to act in an intelligent way, the choice of a

strategy that is pertinent or effective for the resolution of problems; the supervision and control of

mental activity, and the regulation of the cognitive powers that make human learning possible. This

mental activity, control and regulation demands: a) to plan the activity before reaching the solution of a

problem, b) to observe the efficiency of the initiated activity, c) to integrate the knowledge and skills

that intervene in the planned solution and d) to verify the results (Sengul & Katranci, 2015; Cruz, 2002;

Tesouro, 2005; Sáiz-Manzanares & Montero-García, 2015).

3.2. Metacognition and socioformation

Socioformation is an educational approach for the integral formation of an individual. The learning

is approached as formation, which is made within a collaborative process of problem-solving that

makes self-realisation, co-existence, socioeconomic development and environmental sustainability

possible. The formation needs of the identification, interpretation, argument and resolution of a

problem’s context. It is evaluated by means of the record of the performance of the students facing

problems, in the framework of collaborative processes and metacognitive performance (Tobon, 2015).

From the perspective of socioformation, metacognition is an essential aspect. It enables us to learn

of our cognitive processes and metacognitive skills, to constantly improve performance in our actions

on the basis of critical and constructive reflection, being necessary the monitoring for the control and

the auto-regulation of the integral actions. Metacognitive strategies consist of a set of action plans that

make the knowledge of mental processes, such as planning, monitoring and evaluation possible, in

agreement with certain aims (Tobon, 2013). With an emphasis on collaborative work and evaluation by

means of evidences in the process of teaching and learning, metacognition must be promoted as a

method parallel to the learning of the discipline.

Socioformation arises from the needs of students that must learn to face challenges involving

analysis, argument and interpretation, and allows them to try to solve problems in different contexts. In

this direction, a problem consists of the challenge of achieving an anticipated or ideal situation from existing information in an environment with sense (the student’s own person, family, community,

social, environmental, scientific, technological, recreational, cultural, etc.), by analysing the options of

solution and looking for the achievement of a result.

In order to confront the problems of context it is necessary for the student to exercise

comprehension, interpretation, the exposition of a solution, arguments and resolution, based on the

goals of formation outlined in the curriculum and in the discipline of the classroom, regarding the

needs and expectations of the students and the educational challenges. To face problems, it is necessary

that the students learn to identify, to interpret, to argue and to solve them, managing the actions and

resources necessary for achievement (Hernandez-Mosqueda, Guerrero-Rosas & Tobon-Tobon, 2015).

Mathematics is a fundamental part of the curriculum of an engineer. The discipline is normally

taught in the first semesters of the academic programme and contributes to providing tools for the

acquisition of knowledge of other areas and at the same time forming skills that the student needs for

his performance in personal and working life.

3.3. Problems solving

In the mathematics classroom, the approach to resolution of problems motivates and feeds the

students’ mathematical learning in a significant way. This mathematical practice gives form to the

concepts, gives sense and meaning to the processes and the values, promoting in this way a

transformation of the technologies or forms of knowledge (Intaros, Inprasitha & Srisawadi, 2014).

In relation to the problems of context, this can be a social, working or real-life context, the method

of confronting them supposes three basic processes: the creation of a mathematical model which

represents the situation of the problem, the application of technologies and mathematical knowledge to

the model within a mathematical dimension, and the decoding of the real situation to analyse the

relevance and validity of the solution (Cruz, 2002).

See Full Size >

In this way, the work with the solution of problems develops and promotes a set of features and

personality qualities, which are reflected in the attitude, feelings, emotions, beliefs and collaborative

work of the students (Cruz, 2002). In addition, the process of solution of mathematical problems can be

a learning strategy that applies to all subjects, since every problem that appears can refer to any content

or discipline. In the same way as solving a mathematics problem, if the student manages to give it

sense and meaning, the transfer to other disciplines is realised in a direct way.

The idea of ‘problem’ is very diverse (Sengul & Katranci, 2012; Perez & Ramirez, 2011;

Hernandez-Mosqueda, Guerrero-Rosas & Tobon-Tobon, 2015; Dostal, 2015). For this research, it is

assumed to be: a theoretical or practical difficulty that is required to be solved and that causes an

inquisitive attitude in an individual, promoting mental activity that stimulates the aptitude to create,

invent, reason and analyse situations to reach a goal or purpose.

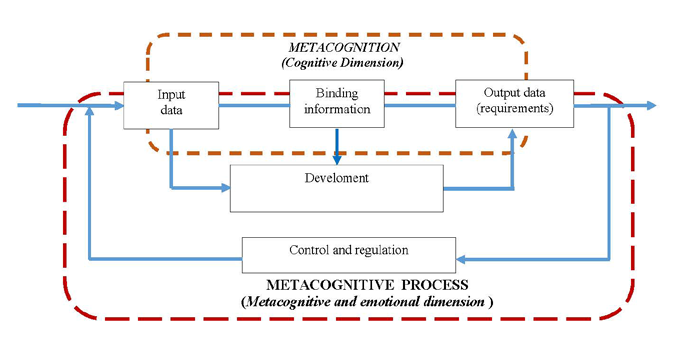
In order to characterise problem-solving, according to Beyer (1998), Kilpatrick and Mayer in (Perez

& Ramirez, 2011) fig. 2, it is possible to consider the problem to be a statement containing the

following three elements: information of entry, that is the initial information; information of exit, or the

problem requirements, and binding information, which would be the concepts and theories belonging to

the cognitive dimension. This approach presents a map to continue to the solution of the problem. The

student identifies the problem, the requirements and the theoretical information, algorithms and

concepts involved. It is recommended that the student makes a drawing or scheme of the situation

articulating these elements. The development must follow the set map. In this case, it is proposed that

the cognitive dimension be managed by means of the representation of different registers of semiotic

representation, since in this way a superior order of thought is stimulated (Rodriguez, Nambo &

Aniceto, 2015).

3.4. Exemplification

An example of the work that might be carried out in the classroom with students is shown in fig. 3 .

The figure suggests that with this methodology it is possible to do from an exercise a problem. The

problem must be a situation that provokes and activates the mental work of the student and not a

question that is solved in a mechanical way (Perez & Ramirez, 2011). In this case, the student works

collaboratively. He starts by identifying the data and the requirements of the problem, then he must

integrate theory, concepts and information in order to propose a way to achieve the required result.

The student must resolve the problem, compromising himself in a strong cognitive activity.

Normally, students are not taught how to solve problems in the classroom on a daily basis. By means of

the valuation in the socioformative approach, a way to promote the solution of problems is offered and,

in a parallel way, this induces the students in a metacognitive process through an evaluation instrument,

for example, a checklist (Rodriguez-Peralta, Nambo, Aniceto-Vargas & Viveros, 2015).

3.5. Evaluation and metacognition

In the socioformative approach, the evaluation is directed towards a formative process through

continuous assessment. This formative process must go beyond having the results of learning, evidence

and instruments. In addition, the student’s rhythm of formation, learning and investigation strategies,

how he integrates his knowledge, how he becomes conscious of his way of learning, determining his

previous knowledge, exploring his expectations and goals must be considered. The aim is to form and

improve the student’s performance, promoting methodologies or skills to be developed in a constant

way, looking for improvement day after day for the solution of problems of any context.

See Full Size >

In the process of socioformative valuation, auto-evaluation, co-evaluation and hetero-evaluation are

considered. Activities that allow the promotion of a metacognitive process in the classroom take place

when the teacher accompanies the student interacting between three dimensions: the cognitive, the

metacognitive and the affective dimension (Rodriguez-Peralta, Nambo & Aniceto-Vargas, 2016).

Auto-evaluation: the student turns into the actor of his own learning, promoting self-knowledge in

his way of learning, abstracting, identifying and considering problems, integrating information with

theory, concepts and disciplinary methodologies, activating the processes of feedback and regulation

(tutored by the teacher) and interpreting the valuation as a way for his personal growth (metacognitive

process).

Co-evaluation is made between couples by means of the promotion of collaborative work. Self-

esteem is promoted, together with respect and assertiveness, the reflexive and constructive critique

focuses on the performance and not on the person. There solidarity commitment with his classmates,

the knowledge socialisation with the goal of contributing to the integral growth with and between the

classmates.

Hetero-evaluation is made at first by the teachers (this can be directives or some another actor of the

formative process) that, from their valuation of the students, acquire criteria to implement actions for

the improvement of the formative activities, in the evaluative processes, in the instruments and the

goals that must be achieved (Tobon, Pimienta & Garcia, 2016).

Conclusion

From the documentary analysis made by means of the conceptual cartography the following points

can be considered: The integral formation of a professional must be conformed through all the subjects of thecurriculum, feeding the graduate profile across the discipline’s knowledge and the transverse competence as: to learn to learn, autonomy in learning, the resolution of context problems by means of the integration of information, skills, methodologies, applied in practice with ethical and social commitment, and in a process of constant and permanent improvement. This implies that the student must incorporate a metacognitive process throughout his academic life, turning this process into an essential part of any competence.

This way the mathematical dimension must feed the integral formation. The work of themathematics teacher in the higher education classroom must not be concentrated on the conceptual development of the specific discipline, but he must promote problem-solving skills in any context, as a complex competence that brings into play the cognitive, affective and metacognitive dimensions.

The management of the process of teaching and learning in the classroom must promote in aparallel way the metacognitive process, such that the student is aware of this in his everyday life. One way of promoting it is through the resolution of problems under the perspective of socioformative evaluation.

The socioformative evaluation allows the promotion of integral formation, identifying the student’s weaknesses and promoting their achievements for a constant improvement through collaborative work and commitment to society, promoting the apprehension of a metacognitive process, all mediated through the teacher’s activities.

Acknowledgements

This study is part of the Project: “ The Metacognitive Process for the Constant Improvement of the Academic Performance of the Student from Basic Sciences”, assigned the record number SIP:20161175, IPN, and the PhD Program: Socioformation and Knowledge Society, offered by the University Center CIFE, México.

References

1. Beyer, W. (1998). Algunas precisiones acerca de la resolución de problemas y de su implementación en el aula.
2. Paradigma, Vol. XIX, N 1, Junio de 1998/1-10 Cruz, M. (2002). Estrategia Metacognitiva en la Formulación de Problemas para la Enseñanza de la Matemática. Tesis doctoral no publicada. Instituto Superior Pedagógico de Holguín.
3. Dóstal, J. (2015). Theory of problem solving. Sakarya University Procedia-Social and Behavioral Sciences, 174(2015), 2798-2805 Hernández-Mosqueda, J., Guerrero-Rosas, G., & Tobón-Tobón, S. (2015). Los problemas del contexto: base filosófica y pedagógica de la socioformación. México Ra Ximhai, 4(11), Julio-Diciembre, 125-140.
4. I.P.N. (2004). Un Nuevo Modelo Educativo para el IPN. Serie: Materiales para la Reforma. Vol. 1 First Edition. México: Ed. Publicaciones.
5. Intaros, P., Inprasitha, M., & Srisawadi, N. (2014). Students ‘problem solving strategies in problem solvingmathematics classrooms. Thailand Procedia-Social and Behavioral Sciences, 116 (2014), 4119-4123.
6. Pérez, Y., & Ramírez, R. (2011). Maths solving problem strategies. Theoretical and methodological foundations. Revista de Investigación, 73(35), Mayo-Agosto.
7. Rodríguez, L., Aniceto, P., & Rojo, M. (2013). Competencias, metacognición y matemáticas. Caso de estudio en el nivel superior. Memorias del III Congreso Internacional de Experiencias en la Formación y Evaluación de Competencias. CIFCOM. Mexico.
8. Rodríguez, L., Nambo, S., & Aniceto, P. (2015). Mathematics in the Classroom: Conceptual Cartography of Differential Calculus. Revista Romaneasca pentru Educatie Multidimensionala, 7(2), 47-54. Doi: DOI: 10.18662/rrem/2015.0702.04 Rodríguez-Peralta, L., Nambo, S., & Aniceto-Vargas, P. (2016). La evaluación en un proceso metacognitivo en el aula de matemáticas. Caso de estudio. In Congreso Iberoamericano Kaanbal, México.
9. Rodríguez-Peralta, L., Nambo, S., Aniceto-Vargas, P., & Viveros, P. (2015). Lista de cotejo: una estrategia para el desarrollo del pensamiento matemático avanzado. V Congreso Internacional de Formación y Gestión del Talento Humano CIFCOM2015. México.
10. Sáiz-Manzanares, M., & Montero-García, E. (2015). Metacognition, Self-regulation and Assessment in Problem-Solving Processes at University. In A. Peña-Ayala, Metacognition: Fundaments, Applications, and Trends, Springer International Publishing Switzerland, pp. 107-133. DOI 10.1007/978-3-319-11062-2_5.
11. Sengul, S., & Katranci, Y. (2015). Meta-cognitive Aspects of Solving Indefinite Integral Problem. Turkey. Procedia-Social and Behavioral Sciences, 197(2015), 622-629.
12. Sengul, S., & Katranci, Y. (2012). Metacognitive aspects of solving function problems. Procedia-Social and Behavioral Sciences, 46, 2178-2182.
13. Schoenfeld, A. (1987). What’s all the fuss about metacognition?. Cognitive science and mathematics education.Vol. 189. A. H. Schoenfeld (Ed.) Tesouro, M. (2005). La metacognición en la escuela: la importancia de enseñar a pensar. España. Educar, 35, 135-144.
14. Tobón, S. (20001).Aprender a emprender: un enfoque curricular. Medellín: Funorie.
15. Tobón, S., et al. (2015). The Socioformation: a Conceptual Research. México. Paradigma, XXXVI(1), 7–29. Tobón, S. (2013). Formación integral y competencias. Pensamiento complejo, currículo, didáctica y evaluación. 4ª. Colombia: Ed. Ecoe-ediciones.
16. Tobón, S. (2012). Cartografía Conceptual: estrategia para la formación y evaluación de conceptos y teorías.
17. Retrieved from: https://issuu.com/cife/docs/e-book__cartograf__a_conceptual Tobón, S. (2004). Cartografía Conceptual. Spain: Cyber Educa.
18. Tobón, S., Pimienta J., & Garcia, J. (2016). Secuencias didácticas y socioformación. Pearson Educación de México, S.A. de C.V. México.