Development research and methods for aluminum industry optimization

Abstract

This paper shows an original method for aluminum’ making optimization. This method is based on the analysis of the functional and technological performances of specific furnaces, using mathematic modeling of respective processes. The papers have as a starting point main principles of mathematical modeling of aluminum technological processes on the basis of these modeling principles the optimization possibilities of aluminum elaboration in the specific furnaces are analyzed. The main results presented in the papers are based on the modeling flow chart of the aluminum technological processes, which is thoroughly described in the paper.

Keywords: development methods, research methods, management, aluminum, modeling

1.Introduction

Mathematical modeling of the aluminum’s technological processes for the optimization of the functional and technological performances of this complex unit is based on the next principles (Ioana, 2007; Ioana, & Nicolae, 2002; Ioana, & Semenescu, 2013): A. – consists in observing and analysing competently the modelated reality, using both analogy with other fields of research and logical homology.

According to this principle, for mathematical models making were used the following steps:

• The modelated subject definition – represents the first phase of the modelation analysis. This step must satisfy both the purpose and the simultaneous system’s aims, assuring their compatibility;
• The effiency criterias definition – is a step imposed on the correct definition of the system’s aims and allows the optimization of the modelling solutions;
• Making the options – basing on accessing some realistically, original and efficient solutions;
• Choices evaluating – related to the established efficiency criteria’s;
• Choosing the final solution – based on the analysis between the different solutions of the modeling.

B. – is based on the sistems’theory, including feed-back concept. C. The principle of hierarchisation – consists of making hierarchical models systems, for structuring the decision and coordinating the interactive subsystems.

The Concept of the Block Diagram for the Modeling System

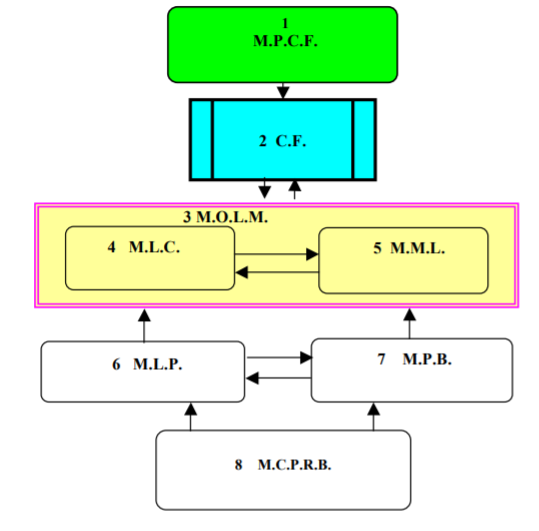
It was conceived, based on these modelling principles, the block diagram for the modelling

system of the electric arc furnace’s respective processes, presented in figure 1.

The modeling system’s central element of the aluminum’ technological processes conceived consists of the system’s criteria function (Adams, 1975; Semenescu et al., 2006). Knowing that the technological processes study for EAF is subordinated to high quality steel obtaining, the modelling system’s criteria function (CF) is the ratio between Quality and Price (equation 1):

CF= ${\left(\frac{QUALITY}{PRICE}\right)}_{max}$(1)

The maximum of the criteria function is assured by its prescribing mathematical model

(M.P.C.F.).

The modelling system conceived for the EAF processes is composed of six subsystems (Adam, 1983; Lenk, 1984), represented by the following mathematical models:

• The mathematical model of prescribing the criteria function (M.P.C.F.)
• The mathematical model of loading’s calculation (M.L.C.)
• The mathematical model of the melting’s effective leading (M.M.L.)
• The mathematical model of loading’s preheating (M.L.P.)
• The mathematical model reactive powders’ blowing (M.P.B.)
• The mathematical model designing calculation for the preheating’s recuperative burners (M.C.P.R.B.)

See Full Size >

The importance of the cause and effect relationship of the transfer function is evidenced by the

interest in representing the relationship of the system variables by diagrammatic means.

In figure 2 is presented the scheme of general block for 2 inputs and 2 output system.

See Full Size >

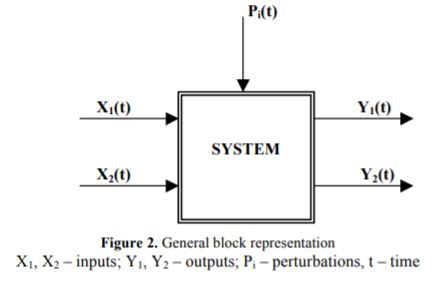
The block diagram representation of the system relationship is prevalent in control system engineering. Block diagram consists of unidirectional operational blocks, that represent the transfer function of the variables of interest.

Results and Conclusions

The mathematical model of prescribing the criteria function concept consists of transforming the criteria function (CF) in quality-economical matrices $M_{QE}$, as in the scheme presented in figure 3

See Full Size >

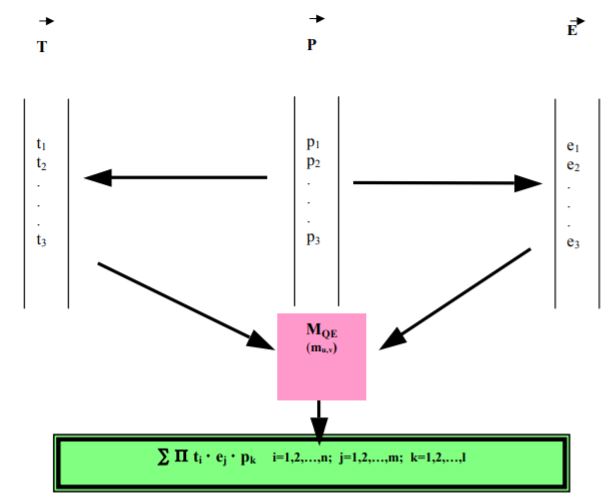
The levels of prescribing the criteria function can be obtained by using a composition algorithm for three vectors:

• T- vector – technical parameters’ vector (ti);
• E- vector – economical parameters’ vector (ej);
• P- vector – weight vector (p1).

The components of two vectors T and E witch are considered to have important weight in the criteria function’s evaluation are:

• t1 – the aluminum chemical composition;
• t2 – the aluminum purity (in gases);
• t3 – the aluminum purity (inclusions);
• e1 – the specific consumption of basic material and materials;
• e2 – the specific consumption of energy;
• e3 – the elaboration process’s productivity in specific furnace.

Acknowledgements

This work has been funded by the Sectorial Operational Programme HumanResources Development 2007–2013 of the Ministry of European Funds through the Financial Agreement POSDRU/159/1.5/S132395 and Financial Agreement POSDRU/159/1.5/S/134398.

References

• Ioana, A., Semenescu, A. (2013). Technological, Economic, and Environmental Optimization of Aluminum Recycling, JOURNAL OF THE MINERALS, METALS & MATERIALS SOCIETY, JOM: Volume 65, Issue 8/2013, ISSN 1047-4838 (ISI-Web of Science/Science Citation Index Expanded), 951-957.

• Ioana, A. (2007). Managementul producţiei în industria materialelor metalice. Teorie şi aplicaţii, Ed. PRINTECH, Bucuresti, (ISBN 978-973-718-758-1).

• Ioana, A., Nicolae, A. (2002). Optimal Managing of Electric Arc Furnaces, Ed. Fair Partners Publishing, Bucharest, (ISBN Code 973-8470-04-8).

• Semenescu, A., Oprescu, I., Mirea, V., Semenescu, C.V., Florea, B., Bălescu, C. (2006) Control of Technological Process for Materials Processing, Ed. Printech, Bucharest.

• Adams, L.F. (1975). Engineering measurements and instrumentation, EU. Press, London.

• Adam, H. (1983). Instrument Science and Technology, Vol. 2, Ed. B.E. Jones, London.

• Lenk, J.D. (1984). Handbook of Microcomputer Based Instrumentation and Control, Prentice-Hall International, Hemel Hempsead.