Installation For Making Fried Crill Ice Cream

Element Peltier and the principle of its operation

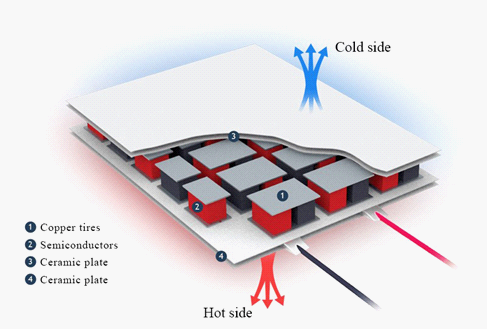
The Peltier element is a thermoelectric converter, the principle of operation of which is based on the Peltier effect - the appearance of a temperature difference when an electric current flows (Bulat & Buzin, 2001). In the English-language literature, Peltier elements are designated TEC (from the English Thermoelectric Cooler - thermoelectric cooler). The device has two sides, and when a constant electric current flows through the device, it transfers heat from one side to the other, so one side cools and the other heats up (Figure 1).

The structure of the Peltier Element is based on one or more pairs of small semiconductor parallelepipeds - one n-type and one p-type, connected in pairs using metal jumpers. Metal bridges simultaneously serve as thermal contacts and are insulated with a non-conductive film or ceramic plate. Pairs of parallelepipeds are connected in such a way that a series connection of many pairs of semiconductors with different types of conductivity is formed, so that at the top there are one sequence of connections (n-> p), and opposite ones below (p-> n). Electric current flows sequentially through all parallelepipeds. Depending on the direction of the current, the upper contacts are cooled, and the lower ones are heated - or vice versa. Thus, the electric current transfers heat from one side of the Peltier element to the opposite and creates a temperature difference. If you cool the heating side of the Peltier element, for example, with a radiator and a fan, then the temperature of the cold side becomes even lower. In single-stage cells, depending on the cell type and current, the temperature difference can be up to approximately 70 ° C (Korzun et al., 2014).

See Full Size >

Calculation of the required cooling capacity for the installation

Initial data for the calculation:

Pasta from krill is laid out on the work surface of the freezer at a temperature of ${\mathrm{t}}_1=6\mathbf{°}\mathrm{C}$ ; and is extracted from it at a temperature ${\mathrm{t}}_2=-18\mathbf{°}\mathrm{C}$ ; the specific heat of krill is equal to $C_{cm}=\mathrm{0,889}\mathrm{}\mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}\mathbf{/}\mathrm{k}\mathrm{g}\mathbf{·}\mathbf{°}\mathrm{C}$; the specific heat of semi-frozen paste to $C_m=\mathrm{0,721}\mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}\mathbf{/}\mathrm{k}\mathrm{g}\mathbf{·}\mathbf{°}\mathrm{C}$; the mixture contains 30.7% of water; W = 0,307; freezing pasta is (cryoscopic temperature) ${\mathrm{t}}_3=-\mathrm{3,6}\mathbf{°}\mathrm{C}$ (Nikolaev & Nikolaev, 2013).

Calculate the percentage of frozen water using the formula:

$W_l=(\mathrm{1}-\frac{t_{\mathrm{3}}}{t_{\mathrm{2}}})\mathrm{}\times \mathrm{}\mathrm{100}$

After substituting the original data into the formula, we get:

$W_l=\left(\mathrm{1}\mathrm{}-\frac{-\mathrm{3.6}}{-\mathrm{18}}\right)\times \mathrm{100}=\mathrm{80}\mathrm{\%}$

The consumption of cold in the freezer is determined by the formula:

$\mathrm{q}=q^{\mathrm{\text{'}}}+q^{\mathrm{\text{'}}\mathrm{\text{'}}}$

The value of the specific cold consumption for cooling the mixture is calculated by the formula:

$q^{\mathrm{\text{'}}}={\mathrm{C}}_{\mathrm{c}\mathrm{m}}\left({\mathrm{t}}_{\mathrm{1}}-{\mathrm{t}}_{\mathrm{3}}\right)$

$q^{\mathrm{\text{'}}}=\mathrm{0,889}\left(\mathrm{6}-(-\mathrm{3,6})\right)=\mathrm{8,53}\mathrm{}kcal\mathrm{}/\mathrm{}kg$

The specific consumption of cold for freezing the mixture is determined by the formula:

$q^{\mathrm{\text{'}}\mathrm{\text{'}}}=C_m\left(t_{\mathrm{3}}-t_{\mathrm{2}}\right)+\mathrm{80}\frac{W}{\mathrm{100}}\frac{W_l}{\mathrm{100}}$

$q^{\mathrm{\text{'}}\mathrm{\text{'}}}=\mathrm{0,721}\left((-\mathrm{3,6})-(-\mathrm{18})\right)+\mathrm{80}\frac{\mathrm{0,307}}{\mathrm{100}}\frac{\mathrm{0,8}}{\mathrm{100}}=\mathrm{10,384}\mathrm{}kcal\mathrm{}/\mathrm{}kg$

Cold consumption in the freezer:

$q=\mathrm{8.53}+\mathrm{10.384}=\mathrm{18.914}\mathrm{}kcal\mathrm{}/\mathrm{}kg=\mathrm{79.2}\mathrm{}kJ\mathrm{}/\mathrm{}kg$

After conducting the experiment, it turned out that within 5 minutes you can cook about 0.2 kilograms of the product, we determine how much product you can cook in an hour:

$\mathrm{G}=\mathrm{0.2}\times \mathrm{12}=\mathrm{2.4}\mathrm{}kg\mathrm{}/\mathrm{}h$

Required cooling capacity:

$Q_{\mathrm{0}}=q\bullet G$

Where, $q$ - cold consumption in the freezer, $kJ/kg$, $G$ - freezer productivity, $kg/h$.

$Q_{\mathrm{0}}=\mathrm{79.2}\times \mathrm{2.4}=\mathrm{190}\mathrm{}kJ\mathrm{}/\mathrm{}h=\mathrm{52.77}\mathrm{}W$

As a result of the calculations, the required power of the freezer for the manufacture of fried krill ice cream was determined, which amounted to 52.77 W.

Calculation of Peltier elements

The elements were calculated based on the selection of the following initial data: thermo-element length $l=40mm$; section $S=5,5{mm}^2$; quality factor of the material $Z=3\bullet {10}^{-3}{K}^{-1}$; thermo-EMF coefficient $\alpha =\mathrm{3,7}\bullet {10}^{-4}V/K$; electrical conductivity coefficient $\sigma =8\bullet {10}^4{Ohm}^{-1}\bullet m^{-1}$; required cooling capacity $Q_0=\mathrm{52,77}W$; operating conditions $T_c=251K$, $T_h=313K$ (Patrusheva et al., 2013).

We determine the optimal current by the formula (Pnevsky et al., 2018):

$I_{opt}=\alpha \times \mathrm{}{T}_{\mathrm{с}}\times \sigma \times \left(\frac{S}{\mathrm{2}\times l}\right)$

Where, $\alpha$ - is the coefficient of thermo-EMF, V/K, $T_{с}$ - is the temperature of the cold side of the element, $K$, $\sigma$ - is the coefficient of electrical conductivity, ${Ohm}^{-1}\bullet m^{-1}$, $S$ - section, ${mm}^2$, $l$ - element length, mm.

${\mathrm{I}}_{opt}=\mathrm{3,7}\bullet {\mathrm{10}}^{-\mathrm{4}}\bullet \mathrm{251}\bullet \mathrm{8}\bullet {\mathrm{10}}^{\mathrm{4}}\bullet \frac{\mathrm{0.0000055}}{\mathrm{2}\bullet \mathrm{0,004}}=\mathrm{0,51}\mathrm{}\mathrm{A}$

We determine the voltage drop by the formula:

$U_{\mathrm{0}}=\alpha \times T_c$

Where, $\alpha$ - is the coefficient of thermo-EMF, V/K, $T_c$ - is the temperature of the cold side of the element, $K$.

$U_{\mathrm{0}}=\mathrm{3,7}\bullet {\mathrm{10}}^{-\mathrm{4}}\bullet \mathrm{251}=\mathrm{0,092}\mathrm{}V$

We determine the refrigeration coefficient by the formula:

${\epsilon }_d=\frac{\mathrm{1}}{{\mathrm{2}T}_h}\times (T_c-\frac{\mathrm{2}\times \left(T_h-T_c\right)}{Z\times T_c})$

Where, $T_c$ - is the temperature of the cold side of the element, $K$, $T_h$ - is the temperature of the hot side of the element, $K$, $Z$ - is the figure of merit of the material, $K^{-1}$.

${\epsilon }_d=\frac{\mathrm{1}}{\mathrm{2}\bullet \mathrm{313}}\bullet \left(\mathrm{251}-\mathrm{}\frac{\mathrm{2}\bullet \left(\mathrm{313}-\mathrm{251}\right)}{\mathrm{3}\bullet {\mathrm{10}}^{-\mathrm{3}}\bullet \mathrm{251}}\right)=\mathrm{0,137}$

We determine the resistance of the thermocouple by the formula:

$R_{\mathrm{0}}=\mathrm{2}\bullet l/\sigma \bullet S$

Where, $\sigma$ - electrical conductivity coefficient, ${Ohm}^{-1}\bullet m^{-1}$, $S$ - section, ${mm}^2$, $l$ - element length, mm.

$R_0=\frac{2\bullet \mathrm{0,04}}{\mathrm{8}\bullet {\mathrm{10}}^{\mathrm{4}}\bullet \mathrm{0.0000055}}=\mathrm{0,182}\mathrm{O}\mathrm{h}\mathrm{m}$

We determine the cooling capacity of the thermocouple by the formula:

$Q^{\mathrm{\text{'}}}=\frac{{\alpha }^{\mathrm{2}}}{R_{\mathrm{0}}}\times (\frac{T_c^{\mathrm{2}}}{\mathrm{2}}-\frac{T_h-T_c}{Z})$

Where, $\alpha$ - is the thermo-EMF coefficient, V/K, $T_c$ - is the temperature of the cold side of the element, K, $T_h$- is the temperature of the hot side of the element, K, $Z$ - is the figure of merit of the material, $K^{-1}$, $R_0$- is the resistance of the thermocouple, Ohm.

$Q^{\mathrm{\text{'}}}=\frac{{(\mathrm{3,7}\bullet {\mathrm{10}}^{-\mathrm{4}})}^{\mathrm{2}}}{\mathrm{0,182}}\bullet \left(\frac{{\mathrm{251}}^{\mathrm{2}}}{\mathrm{2}}-\frac{\mathrm{313}-\mathrm{251}}{\mathrm{3}\bullet {\mathrm{10}}^{-\mathrm{3}}}\right)=\mathrm{}\mathrm{0,008}\mathrm{}W$

We determine the number of thermocouples by the formula:

$N=Q_{\mathrm{0}}/Q^{\mathrm{\text{'}}}$

Where, $Q_0$ - is the required cooling capacity, W, $Q^{\text{'}}$ - is the cooling capacity of the thermocouple, W.

$N=\frac{\mathrm{52,77}}{\mathrm{0,008}}=\mathrm{6596}$

Determine the power consumed by one thermocouple using the formula:

$P_{\mathrm{0}}=Q^{\mathrm{\text{'}}}/{\epsilon }_d$

Where, $Q^{\text{'}}$- thermocouple refrigerating capacity, W, ${\epsilon }_d$ - coefficient of performance.

$P_{\mathrm{0}}=\frac{\mathrm{0.008}}{\mathrm{0.137}}=\mathrm{0.0583}\mathrm{}W$

We determine the power of the power supply by the formula:

$P=P_{\mathrm{0}}\bullet N$

Where, $P_0$ - is the power consumed by one thermocouple, W, $N$ - is the number of thermocouples.

$P=\mathrm{0.0583}\times \mathrm{6596}=\mathrm{385}\mathrm{}W$

We determine the heat of hot junctions by the formula:

$Q_h=P+Q_{\mathrm{0}}$

Where, $P$ - is the power of the power supply, W, $Q_0$ - is the required cooling capacity, W.

$Q_h=\mathrm{385}+\mathrm{52.77}=\mathrm{438}\mathrm{}W$

We determine the voltage of the power source by the formula:

$U_p=U_{\mathrm{0}}\times N$

Where, $U_0$ - is the voltage drop, V, $N$ - is the number of thermocouples.

$U_p=\mathrm{0.092}\times \mathrm{6596}=\mathrm{607}\mathrm{}V$

It is proposed to connect all the elements in parallel, this will provide additional reliability of the installation, and if one of the elements fails, the installation will not stop working.

$U_p=\frac{\mathrm{607}}{\mathrm{48}}=\mathrm{12}\mathrm{}V$

The total power should be calculated, taking into account that an additional 15-20% of the power consumed by the elements will be spent on the pump for water cooling, as well as on the fan for air cooling. According to the formula:

${\mathrm{P}}_{gen}=\mathrm{P}+\mathrm{0,15}\bullet \mathrm{P}$

Where, $\mathrm{P}$ - is the power consumed by the elements, W.

${\mathrm{P}}_{gen}\mathrm{}=\mathrm{}\mathrm{385}+\mathrm{0.15}\times \mathrm{385}=\mathrm{443}\mathrm{}\mathrm{W}$

Figure 2, shows the design of the installation on Peltier elements.

See Full Size >

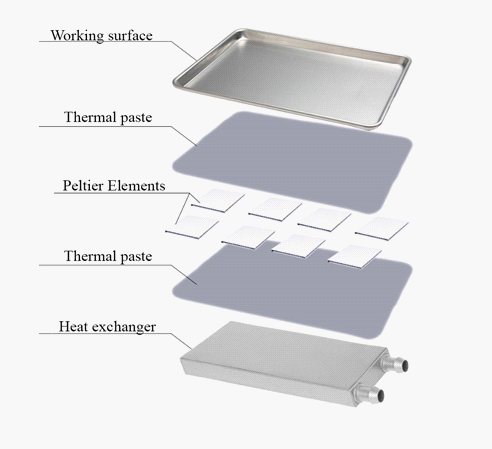
As a thermal paste, it is supposed to use one of the most common. Thermal paste KPT-8 Connector KPT-8, which removes heat from heating elements and improves heat transfer between contacting surfaces. Complies with GOST 19783-74.

Specifications:

• The color of the paste is white;

Figure 3 shows a radiator in which heat energy from the hot side of the unit will be removed.

See Full Size >

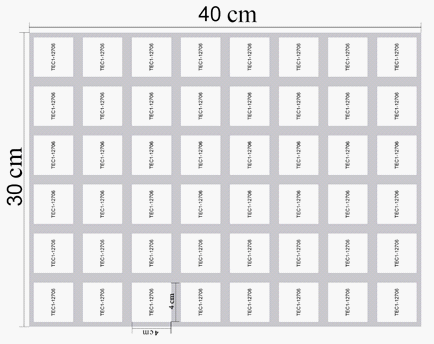
Figure 4 shows arrangement of Peltier elements under the working surface arrangement.

See Full Size >