Abstract
Nowadays, data mining methods are applied in various fields of science and technologies. The widespread application of these methods necessitates the development of procedures to improve the efficiency of basic methods. Often, the efficiency of approaches based on data mining methods significantly depends on the selection of numerical coefficients. Moreover, these numerical coefficients can be both parameters of the algorithm and parameters of the obtained solutions. Therefore, it is possible to apply optimization methods to determine the best values. Nowadays, one of the most efficient methods of real optimization is differential evolution. The paper presents the study the differential evolution application to optimize coefficients of a dynamic system model obtained by an approach based on a self-configuring genetic programming algorithm. Also, it considers optimization of threshold values for solving classification problems with decision trees. The paper considers the most popular methods for training decision trees. The selected tasks demonstrate the universality of the proposed modification, since they solve diverse tasks. Moreover, the applied data analysis methods belong to different classes. The results of numerical experiments are presented for these tasks. They prove efficiency of the proposed hybridization.
Keywords: Differential equation, genetic programming, decision tree
Introduction
Currently, data mining methods are applied in various fields. Only in 2021, the volume of software that apply artificial intelligence algorithms increased by 21.3% compared to 2020 (Artificial intelligence, 2022). This proves the trend of such methods use for solving applied problems. However, these methods are becoming more widespread. So, requirements for the quality of the obtained solutions are increasing as well. Hence, algorithms and procedures are being developed to improve the efficiency of the existing methods. Hybridization of algorithms is one of these fields. Methods to designing neural networks, fuzzy logic systems, decision trees applying evolutionary algorithms are examples of such approaches (Khritonenko et al., 2017; Polyakova et al., 2020).
Nowadays, such an optimization method as differential evolution has gained wide popularity. Differential evolution (DE) is a method of multivariate stochastic optimization of real variables functions. It applies some ideas of evolutionary algorithms (Storn, 1996).
Differential evolution is used not only as an independent tool in solving optimization problems but also in synthesis with the methods of machine learning and artificial intelligence (Mitrofanov & Semenkin, 2019). The paper considers the efficiency of such type of application.
Problem Statement
Data mining methods are defined by parameters, which are often specified by numeric values. The efficiency of the algorithm and the quality of the resulting model depend on the correctness of the selected parameters. Therefore, it is necessary to optimize such values, and consequently, develop procedures that help search for optimal values.
Research Questions
The key questions for the present study is:
- Is it possible to improve the quality of the solution obtained by different methods applying a differential evolution method?
Purpose of the Study
The study investigates the application efficiency of the differential evolution method to optimize numerical parameters in approaches based on data mining.
Research Methods
Currently, the most efficient method of real optimization is a differential evolution method (Storn, 1996).
A population in the DE algorithm is a set of vectors from Rn. Here, each variable of this space corresponds to its attribute. Parameters of the algorithm are a population size N, mutation strength F∈[0; 2] and crossover probability P (Storn, 1996).
At the initialization stage, a population of N random vectors is generated. At each next iteration, the algorithm generates a new generation of vectors by combining vectors of the previous generation according to the scheme presented in Figure 1.
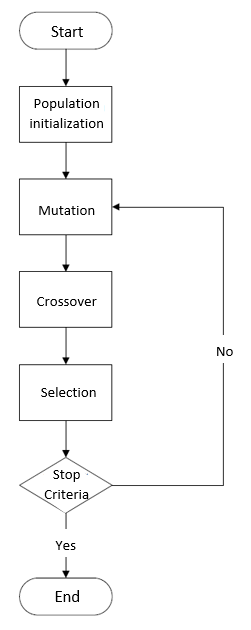
Mutation
At the mutation stage, individuals,, that are not equal to are randomly selected from the population. A so-called mutant vector is generated based on these vectors.
Crossover
The "crossover" operation is performed on the mutant vector. During this operation each coordinate with probability p is replaced by the corresponding coordinate of thevector. The resulting vector is called a trial vector.
Selection
If a trial vector is better than the original, then it takes its place in a new generation.
If a stop criterion is not met, then a new iteration starts.
Application of the differential evolution method in the approach to the dynamical systems identification
The paper (Karaseva & Semenkina, 2021) presents an approach based on a genetic programming (GP) algorithm for identifying a dynamic system in the form of a differential equation. The algorithmic basis of this approach is the genetic programming algorithm characterized by the representation of the solution in the form of a tree (Koza, 1992). The author modifieds the main evolutionary steps. Also, derivatives were included in the terminal set to encode differential equations in the form of a tree. One should take into account that it is required to search for the optimal values of the coefficients included in the equation when representing the solution in the form of a differential equation. The paper compares a basic approach with a hybrid approach that combines genetic programming and differential evolution. The basic method supposes that optimization of numerical coefficients is carried out with the help of steepest descent methods.
Application of the differential evolution method in solving problems of classification by a decision tree
Decision trees are an effective tool in the field of information technology for data analysis (Chistopolskaya & Podolskii, 2022). The main feature of decision trees is the interpretability of the obtained result. It determines their application in banking systems, for example.
However, a decision tree algorithm applies brute force method to optimize thresholds. It makes a decision tree algorithm greedy. The author of the paper studies the efficiency of threshold optimization by the differential evolution method (Mitrofanov, & Semenkin, 2019).
Findings
Efficiency of differential evolution application in the approach to the dynamical systems identification
Objects represented by ordinary differential equations of various orders were selected to test the approach to the dynamic systems identification.
Table 1 presents a comparison of the following approaches. They are identification approach based on a self-configuring GP algorithm and the steepest descent method (let's call it as a "basic" approach), as well as a hybrid approach.
An error of matching the output of the obtained model to the known true values was chosen as an efficiency criterion. Fifty runs were carried out for each task. Table 1 presents average values.
Efficiency of differential evolution application in solving various problems of classification by decision trees
Further, consider the efficiency of differential evolution application in solving various problems of classification by decision trees. Two of the most popular decision tree training methods were chosen for the study, i.e., ID3 and CART (Mitrofanov & Semenkin, 2021). The author calls an algorithm where the selection of the threshold value is carried out by enumeration as a basic algorithm. The author calls an algorithm where the threshold value is optimized by a method of differential evolution as a hybrid algorithm.
Eight classification tasks were selected for the study (Machine Learning Repository, 2022). Classification accuracy was considered as an efficiency criterion; its values are presented in Table 2.
Conclusion
The paper presents the efficiency investigation of applying differential evolution to optimize numerical constants in differential equations describing the behavior of dynamical systems. In this case, the optimization of values included in the result of the approach is considered. The author discusses the possibility of applying differential evolution to optimize the threshold value in decision trees. The approach carries out the selection of the algorithm parameter the final result. According to the conducted studies, it can be concluded that the application of the DE method has significantly increased the efficiency of approaches based on artificial intelligence methods.
Acknowledgments
This work was supported by the Ministry of Science and Higher Education of the Russian Federation (Grant № 075-15-2022-1121).
References
Artificial intelligence (world market). (2022). https://tadviser.com/
Chistopolskaya, A., & Podolskii, V. V. (2022). On the Decision Tree Complexity of Threshold Functions. Theory of Computing Systems, 66(6), 1074-1098. DOI:
Karaseva, T. S., & Semenkina, O. E. (2021). Hybrid approach to the dynamic systems identification based on the self-configuring genetic programming algorithm and the differential evolution method. IOP Conference Series: Materials Science and Engineering, 1047(1), 012076. DOI:
Khritonenko, D., Stanovov, V., & Semenkin, E. (2017). Applying an instance selection method to an evolutionary neural classifier design. IOP Conference Series: Materials Science and Engineering, 173, 012007. DOI:
Koza, J. R. (1992). The Genetic Programming Paradigm: Genetically Breeding Populations of Computer Programs to Solve Problems. MIT Press.
Machine Learning Repository. (2022). https://archive.ics.uci.edu/ml/index.php
Mitrofanov, S. A., & Semenkin, E. S. (2019). Differential Evolution in the Decision Tree Learning Algorithm. Siberian Journal of Science and Technology, 20(3), 312-319. DOI:
Mitrofanov, S. A., & Semenkin, E. S. (2021). Tree retraining in the decision tree learning algorithm. IOP Conference Series: Materials Science and Engineering, 1047(1), 012082. DOI:
Polyakova, A., Leonid, L., & Semenkin, E. (2020). Researching the Efficiency of Configurations of a Collective Decision-making System on the Basis of Fuzzy Logic. In Proceedings of the 12th International Joint Conference on Computational Intelligence, 277-285. DOI:
Storn, R. (1996). On the usage of differential evolution for function optimization. In Proceedings of the Biennial Conference of the North American Fuzzy Information Processing Society (NAFIPS), 519-523). DOI:
Copyright information

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License
About this article
Publication Date
27 February 2023
Article Doi
eBook ISBN
978-1-80296-960-3
Publisher
European Publisher
Volume
1
Print ISBN (optional)
-
Edition Number
1st Edition
Pages
1-403
Subjects
Hybrid methods, modeling and optimization, complex systems, mathematical models, data mining, computational intelligence
Cite this article as:
Karaseva, T. S. (2023). Hybridization of Machine Learning Models and Differential Evolution in Data Mining. In P. Stanimorovic, A. A. Stupina, E. Semenkin, & I. V. Kovalev (Eds.), Hybrid Methods of Modeling and Optimization in Complex Systems, vol 1. European Proceedings of Computers and Technology (pp. 55-60). European Publisher. https://doi.org/10.15405/epct.23021.7

