Abstract
Correspondence (truth) tables are the main model for the analysis of various logical expressions. Their applications go beyond the study of Boolean algebra. The Maple computer algebra system has a wide range of commands for working with propositions, obtaining and evaluating their truth, but the result of their execution is most often not represented in a perfectly normal form. The results obtained are undoubtedly useful, but do not contribute to the development of competencies in the field of modeling Boolean functions. In this case, using the programming methods of the Maple computer algebra system, as well as its ability to create interactive applications. The article presents the results of a study summarizing the experience of implementing computer algebra systems for modeling logical functions. To expand the possibilities, comply with the requirements of interactivity, the Maple computer algebra system was chosen as the main tool. The developed and presented interactive application allows you to automatically build Boolean functions based on their truth or falsity values and present the result in the form of perfect disjunctive or conjunctive normal forms. The authors presented the features of using the developed application. The main goal: to achieve an understanding of the process of building a model of Boolean functions, presented in a perfect disjunctive or conjunctive form, to help in the study of discrete mathematics, students of both technical and humanitarian specialties. In addition, evaluate your knowledge in this discipline.
Keywords: Boolean algebra, correspondence (truth) tables, computer algebra, Maple, perfect normal forms
Introduction
In the era of digitalization of education there is an increasing need to acquire competencies for building models of various types, as well as to increase the effectiveness of teaching basic mathematical disciplines (Abramovich et al., 2016; AbuEloun & Abu-Naser, 2017). In connection with the informatization of all spheres and types of activity, the problem of creating and using special application software and information and communication technologies becomes relevant (Jehlička & Rejsek, 2018; Melievna, 2020). Computer algebra systems are designed for symbolic calculations and allow you to carry out the entire cycle of developing mathematical models or testing hypotheses. Discrete structures, and hence sections of discrete mathematics, are considered fundamental material for the study of computer science, in addition, knowledge of discrete models and the ability to create them are required in many other areas of activity. For example, this is stated in the ACM and IEEE CS report (ACM/IEEE, 2008; Gainsburg, 2013). The Discrete Mathematics course includes various topics covering sets, relations, mathematical logic, Boolean algebra, number theory, counting, graphs and trees, probability, languages, grammar and finite automata, etc. (Eyrikh et al., 2020, 2018; Rosen, 2012).
Mathematical logic is one of the leading disciplines of the mathematical cycle, contributing to the formation of logical thinking, deductive reasoning techniques necessary for the effective assimilation of other disciplines, as well as the construction of various discrete models. Truth (correspondence) tables, in turn, are one of the most obvious elements of formal logic, allowing you to establish the truth or falsity of logical statements. The experience of pedagogical activity has shown that when studying this element of discrete mathematics, certain difficulties arise (description of perfect disjunctive and conjunctive normal forms) (Durcheva & Nikolova, 2018; Mendelson, 2015).
Computer algebra systems can be used as an effective mechanism for building discrete models and solving issues of effective learning (Ionescu, 2021; Moshchenko et al., 2021; Shingareva & Lizarraga-Celaya, 2009).
It is widely believed that computer algebra systems are available for use only in mathematics, but their scope is much wider.
The need for digitalization of education leads to the development of mechanisms for introducing computer algebra systems into the practice of Russian education, and therefore foreign experience in using such systems in modeling and education is important.
For studying and working with correspondence (truth) tables and other discrete models, one of the most powerful tools available is the Maple computer algebra system. Due to its versatility, flexibility, variety of built-in functions, it is one of the most useful systems. It is favorably distinguished by the ability to build interactive applications depending on user requests (Monagan et al., 2009).
Problem Statement
Most Boolean functions are specified in one of the following forms:
- In the form of a verbal description.
- In the form of truth tables (correspondence).
- Numerically.
- In algebraic form.
- In the form of Carnot maps (Vitch diagrams).
- Numbers of working and prohibited (conditional) sets.
- In the form of timing diagrams.
The truth (correspondence) table is one of the most visual forms of representation. It allows the most convenient transition to other forms (Nieto & Ramos, 2016).
However, the analysis of publications allows us to note that the capabilities of the Maple computer algebra system do not provide for the function of representation (transition) from the numbers of true or false values (numerical notation) presented in the truth (correspondence) table. The issue of interactivity in obtaining and analyzing such models is not presented, so the proposed topic is interesting and promising for further research. In particular, obtaining perfect disjunctive or conjunctive normal forms (SDNF, SKNF) of Boolean functions by numbers on which the function takes a value equal to one (numerical sum) or zero (numerical product); presentation of the modeling process in an interactive form.
We will consider each task below.
Obtaining disjunctive or conjunctive normal forms of Boolean functions by numbers
Scientists are doing research in this area. So, Rosen presented the order of describing such a representation, but the proposed method is cumbersome in the description, since each value must be described as true or false values, which with an increase in the number of variables leads to an increase in the number of errors, the modified method (Olenev) is also not without this drawback. That is, despite the possibility of improving the functionality of the Maple computer system for modeling and representing Boolean functions, this problem remains unconsidered.
Interactive submission form
Recently, the requirements for developing demonstrating and modeling programs have been intensifying, and, first of all, the requirements for interactivity, understandability, and simplicity of the interface used are increasing. Scientists such as Bobalova (2019), Durcheva and Varbanova (2017), Klima and Sigmon (2012) widely use the capabilities of the Maple computer algebra system and building interactive applications using the capabilities of the Maplets library.
Nieto and Ramos (2016) suggested building Boolean functions from truth (correspondence) tables using the Mathematica system. But as follows from the research topic, it is proposed to use the Mathematica computer algebra system as the main modeling tool, and in the opinion of the authors, this system has fewer opportunities for introducing and building interactivity elements.
The research results of Olenev et al. (2022a, 2022b), indicate an improvement in the ability to demonstrate, model and understand various sections of discrete mathematics based on wide application as a tool learning - computer algebra systems. The introduction of the best experience is one of the most important priorities in the development of the digitalization of the education system.
Research Questions
The following questions were posed during the study:
- How to use the Maple computer algebra system to make the transition from the correspondence (truth) table to the description of a logical function in numerical form?
- How to implement such a representation in a perfect disjunctive and conjunctive form?
- How to provide automated results?
- What are the features of this presentation?
Purpose of the Study
Presumably, the answers to the above questions will help achieve the goal and will contribute to the development of competencies in modeling and the study of mathematical logic. That is, the purpose of this article is to develop an interactive application that allows the transition from the representation of a logical function in the form of a table (correspondence (truth) to the numerical form of the representation of a logical function in the form of disjunctive or conjunctive normal forms with the condition of facilitating the recording order (information input) and obtaining the result for further transformations.
Research Methods
The authors used the methods underlying the Maple core, as well as the capabilities of the commands for checking, processing and converting formulas into logical statements included in the Logic library. To create interactive applications, various methods of the Maple computer algebra system were used, including the capabilities of the Maplets[Elements] library, namely the functions for creating Button buttons, fields for entering and outputting calculation results, as well as other interactive elements that help to perform the necessary actions.
Description of the logical function in numeric notation
To create a mathematical model of perfect disjunctive and conjunctive normal forms of representing a logical expression according to the truth (correspondence) table, it is necessary to obtain a logical function in the form of a disjunction of minterms or a conjunction of maxterms. If the maxterm or minterm is represented only by a number, then it must be represented as a list of sets where the variables have the value true or false. The following is the program code that allows you to perform this action:
> restart;
> Perevod:=proc(x::nonnegint,vars::list(symbol))
local i, L, m,k,A,j;
uses Logic;
L:= ListTools:-Reverse(convert(x,base,2));
m:= nops(L);
k:= nops(vars);
if m > k then error "This needs %d digits", m end if;
A:=[0 $ (k-m), op(L)];
for j to nops(A) do
if A[j]=1 then A:=subsop(j=true,A) else A:=subsop(j=false,A); end if;
end do:
A;
end proc:
Action check: The logical function depends on three variables a,b,c and it is necessary to represent the set number 7:
> Perevod(7,[a,b,c]);
Program execution response:
[true, true, true]
The program is working correctly.
Representation in perfect disjunctive and conjunctive forms
To demonstrate symbolic solutions to problems of constructing and obtaining perfect normal forms of a logical function, the capabilities of the Maple computer algebra system (the Maplets - Logic library) were used and the following basic algorithms for symbolic calculations were implemented: easy-to-use and analysis form (results can be obtained in various types of representation), as well as obtaining perfect normal forms of a logical function from a truth table (Kirichek & Potekhina, 2021). Obtaining the desired forms is possible using previously developed procedures, for obtaining the maxterm - Maksterm, the perfect conjunctive form - SKNF, for obtaining the minterm - Minterm and, accordingly, for the perfect disjunctive form - SDNF.
Checking the work of the developed procedure:
> Maksterm ([true, true], [x, y]);
The result:
The procedure is working correctly. Similar checks carried out for the SKNF, Minterm and SDNF procedures showed the correctness of their work.
Automated results
The basis for the automated demonstration of the construction of perfect normal conjunctive and disjunctive forms is Maplets[Elements] and, additionally, a mathematical representation of information using the Maplets library function - MathMLViewer (Kirichek et al., 2021). When using this function, the program sets the necessary form for presenting the result and displays it in mathematical form.
Tasks solved by maplet:
- Familiarity with how Maplets works.
- Getting results.
- Getting the help you need.
- What are the features of this presentation?
The following sections and buttons are used to create a graphical interface:
- Four function buttons for functional actions, help and getting to know Matlets.
- There are two fields for entering information necessary for constructing disjunctive and conjunctive normal forms (the numbers of the required sets and variables on which the simulated function depends are indicated.
- Two output fields of information built by SDNF or SKNF. One outputs the result in the format of the Logic library functions, the other in the generally accepted mathematical form.
Findings
Let us demonstrate the results of applying the developed Maplets.
Perfect Disjunctive Normal Form
Figure 1 shows the Maplets "Maplet of building SDNF according to the truth table to the numbers of minterms", demonstrating the derivation of a perfect disjunctive normal form of a Boolean function that takes the value "true" on set 1 and 2. The Boolean function depends on two variables.
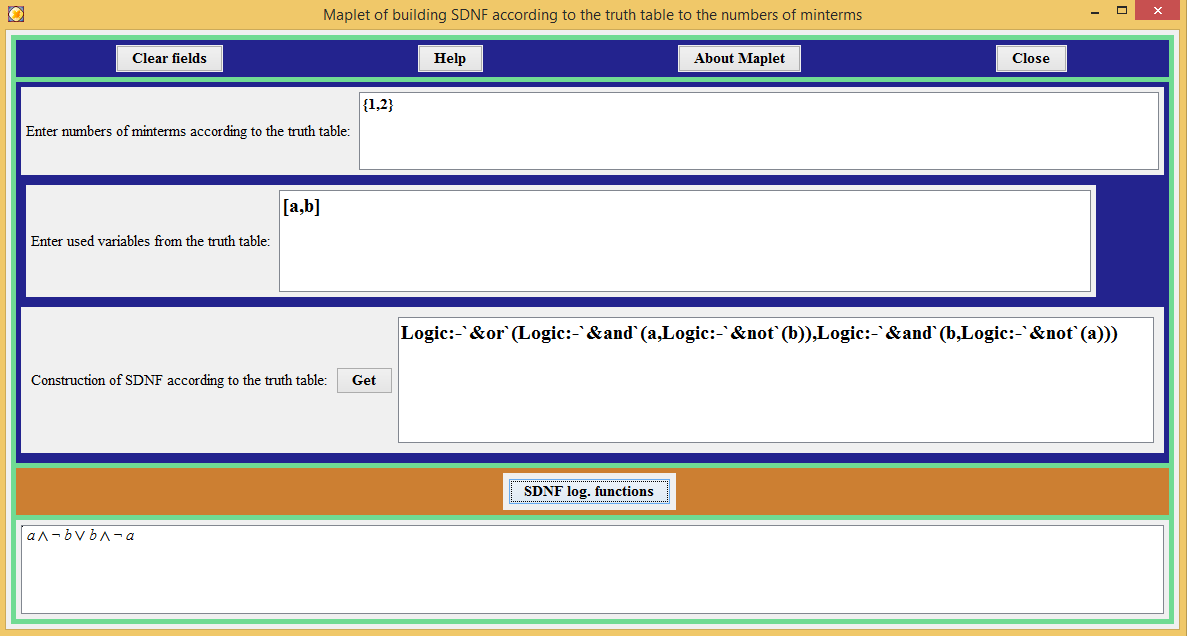
Figure 2 shows the Maplets "Maplet construction of SKNF according to the truth table according to the numbers of maxterms", demonstrating the derivation of a perfect disjunctive normal form of a Boolean function that evaluates to "false" on set 1 and 2. The Boolean function depends on two variables.
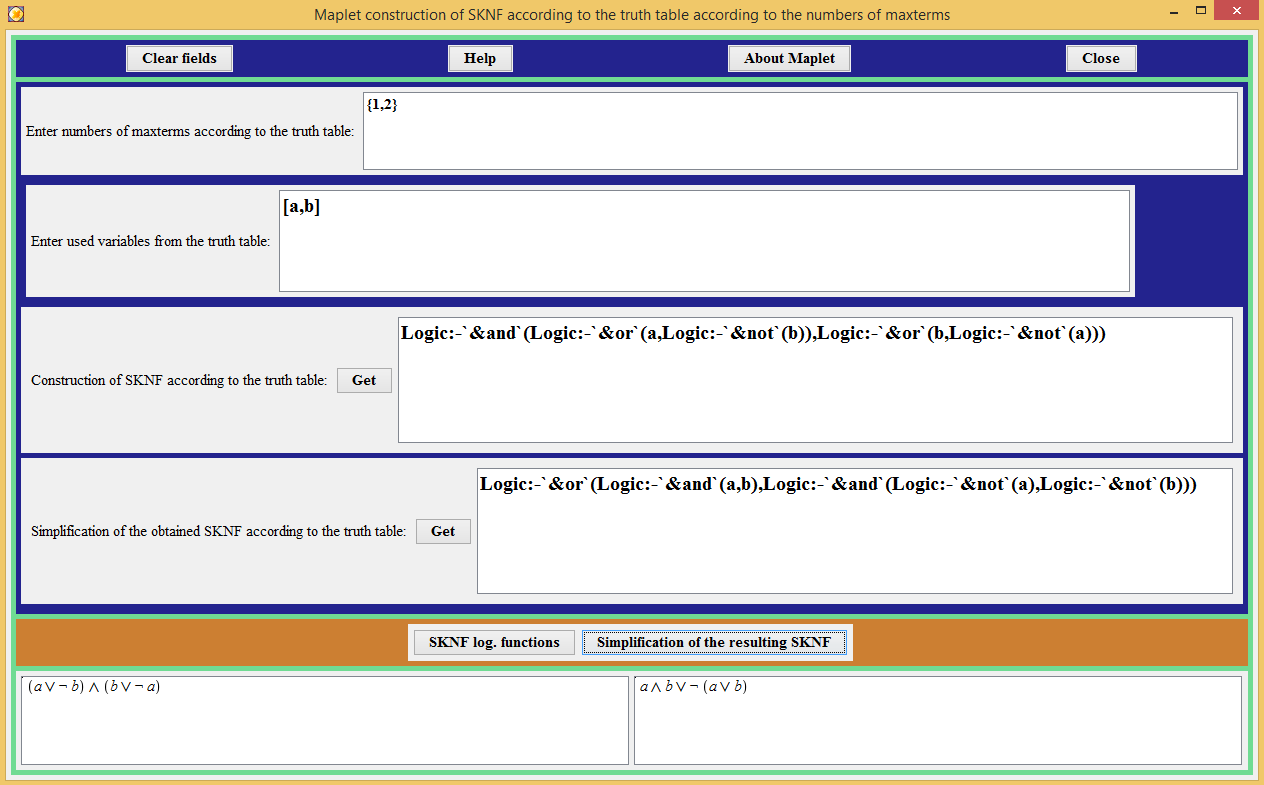
This interactive application additionally has a field for performing the operation of simplifying the resulting logical function.
Conclusion
The Maple computer algebra system is a powerful tool for modeling and teaching mathematical logic, especially for questions of analysis, transformation, simplification and calculus of truth and complex Boolean statements. Correspondence (truth) tables allow us to understand the process of using formal logic, as well as to obtain a perfect disjunctive or conjunctive normal form in various ways from the truth table. However, when the Maple computer algebra system allows you to easily and quickly perform operations on logical expressions, it presents them in a simplified default form and does not use all possible transformations. That is, not all transformation data can be used to perform individual modeling steps or to demonstrate (train) such transformations.
Thus, a procedure was developed that has the ability to demonstrate the process of modeling and obtaining perfect normal forms in a more rational (understandable) way using the capabilities of the Logic library and the built-in Maple programming language, as well as using other features of the Maple system (Maplet library), to build an interactive application that allows in an automated form to make transformations of the correspondence (truth) table. This application allows you to obtain perfect disjunctive or conjunctive normal forms, both in the form of Maple language notations and mathematical form, using a more understandable description of the process of obtaining these forms. We believe that this application can help students studying computer technology during the process of modeling the operation of the simplest nodes of computer technology, self-studying individual sections of discrete mathematics, as well as gaining new competencies in the field of discrete mathematics, mathematical logic, and computer technology. In addition, we believe that the developed application will allow students to improve their understanding of the process of constructing Boolean functions, use the resulting models and improve the possibility of independent study of the subject.
Acknowledgments
We would like to express our appreciation and gratitude to the editorial board for their patience, timely and complete technical and language editing of the research paper.
We welcome any questions, comments, and suggestions for improving the article.
References
Abramovich, S., Burns, J., Campbell, S., & Grinshpan, A. Z. (2016). STEM education: action learning in primary, secondary, and post-secondary mathematics. IMVI Open Mathematical Education Notes, 6, 65-106.
AbuEloun, N. N., & Abu-Naser, S. S. (2017). Mathematics Intelligent Tutoring System. International Journal of Advanced Scientific Research, 2(1), 11-16. http://dstore.alazhar.edu.ps/xmlui/handle/123456789/219
ACM/IEEE. (2008). Computer science curriculum 2008: An interim revision of CS 2001. Report from the interim review task force, ACM and the IEEE CS.
Bobalová, M. (2019). Maple Application in Economic Disciplines. In International Conference at Brno University of Technology, Faculty of Business and Management. (pp. 169-174).
Durcheva, M., & Nikolova, E. (2018). Modeling mathematical logic using MAPLE. AIP Conference Proceedings, 2048(1), 060010. DOI: 10.1063/1.5082125
Durcheva, M., & Varbanova, E. (2017). Applications of CAS in the Teaching and Learning of Discrete Mathematics. Mathematics in Computer Science, 11(3-4), 305-314. DOI:
Eyrikh, N., Bazhenov, R., Gorbunova, T., Markova, N., & Zhunusakunova, A. (2020). The Advantages of Using Computer Algebra System Maple in Learning Differential Equation. In 2020 V International Conference on Information Technologies in Engineering Education (Inforino) (pp. 1-5). IEEE. DOI:
Eyrikh, N. V., Bazhenov, R. I., Markova, N. V., & Putkina, L. V. (2018). Applying Maple Computing Environment in Teaching Mathematics to University Students Majoring in Technical. 2018 IEEE International Conference "Quality Management, Transport and Information Security, Information Technologies" (IT&QM&IS) (pp. 623-628). DOI:
Gainsburg, J. (2013). Learning to Model in Engineering. Mathematical Thinking and Learning, 15(4), 259-290. DOI:
Ionescu, A. (2021). Why computational teaching? The advantage of using the maple software in teaching exact sciences. Atti della Accademia Peloritana dei Pericolanti Classe di Scienze Fisiche, Matematiche e Naturali, 99(S1), A14. DOI:
Jehlička, V., & Rejsek, O. (2018). A Multidisciplinary Approach to Teaching Mathematics and Information and Communication Technology. EURASIA Journal of Mathematics, Science and Technology Education, 14(5). DOI:
Kirichek, K. A., & Potekhina, E. V. (2021). Program for visualization of basic logical operations. Certificate of registration of the computer program 2021613965, 17.03.2021. Russia
Kirichek, K. A., Potekhina, E. V., & Shuvaev, A. V. (2021). Program for visualization and study of mathematical induction. Certificate of registration of the computer program, 2021616997.
Klima, E., & Sigmon, N. P. (2012). Cryptology: Classical and Modern with Maplets. CRC Press.
Melievna, M. D. (2020). Using Information Technology Tools. In Mathematics Lessons for Teaching Future Teachers. International Journal of Scientific & Technology Research, 9(3), 4168-4171.
Mendelson, E. (2015). Introduction to Mathematical logic. CRC Press, Taylor & Francis Group. DOI:
Monagan, M. B., Geddes, K. O., Heal, K. M., Labahn, G., Vorkoetter, S. M., McCarron, J., & DeMarco, P. (2009). Maple Introductory, Programming Guide. Maplesoft, a division of Waterloo Maple Inc.
Moshchenko, I., Nikitenko, O., & Kozlov, Y. V. (2021). Possibility of using CMS Maple to study laws of distribution of random variables. Radiotekhnika/Radio engineering, 204, 128-134. DOI:
Nieto, S., & Ramos, H. (2016). Constructing extended Boolean functions from truth tables using the Mathematica system. International Symposium on Computers in Education (SIIE), 1-6. https://doi.org/
Olenev, A. A., Kirichek, K. A., & Potechina, E. V. (2022a). The Maple Computer Algebra System in Teaching the Basics of Set Theory. Advances in Mathematics Research, 31, 1-39.
Olenev, A. A., Zvereva, L. G., & Saieg, T. H. (2022b). Improving the learning and teaching of mathematical logic elements using maple Journal of Higher Education Theory and Practice, 22(8), 51-57. DOI:
Rosen, K. H. (2012). Discrete mathematics and its applications (7th ed.). McGraw-Hill.
Shingareva, I., & Lizarraga-Celaya, C. (2009). Maple and Mathematica. A Problem Solving Approach for Mathematics. Springer-Verlag. DOI:
Copyright information

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License
About this article
Publication Date
27 February 2023
Article Doi
eBook ISBN
978-1-80296-960-3
Publisher
European Publisher
Volume
1
Print ISBN (optional)
-
Edition Number
1st Edition
Pages
1-403
Subjects
Hybrid methods, modeling and optimization, complex systems, mathematical models, data mining, computational intelligence
Cite this article as:
Olenev, A. A., Petlina, E. M., Shuvaev, A. V., Grivennaya, N. V., & Khabarov, A. N. (2023). Maple Information Tools in the Study of Mathematical Logic Questions. In P. Stanimorovic, A. A. Stupina, E. Semenkin, & I. V. Kovalev (Eds.), Hybrid Methods of Modeling and Optimization in Complex Systems, vol 1. European Proceedings of Computers and Technology (pp. 39-47). European Publisher. https://doi.org/10.15405/epct.23021.5

