System for Automatic Grouping of Metadata of Three-Dimensional Models

Abstract

The purpose of this work is to develop the structure of the algorithm for automatic grouping (clustering) of 3D model metadata which may include model name, dimensions, file size, file format, keywords etc.. The relevance of this work is determined by the need for companies to process complexly structured data, in particular 3D models, and detect groups of similar 3D models for forming their catalogues and other purposes. "similarity", we mean the proximity of objects in a multidimensional space of features, and the problem is reduced to partitioning this space into subspaces of objects so that the objects located in the subspaces form homogeneous groups. We propose an algorithm for automatic grouping of the 3D models based on their metadata, which enables us to group objects according to their numeric and categorical characteristics. The experiments were carried out with the involvement of experts, their evaluation showed the high efficiency of the developed method.

Keywords: OLAP, hypercube, FASMI, multidimensional structure, analytics

Introduction

The purpose of automatic data grouping is to single out homogeneous subsets in the original multidimensional data so that the objects inside the groups are in a certain sense similar to each other, and the objects from different groups differ. By "similarity", we mean the proximity of objects in a multidimensional space of features, and the problem is reduced to partitioning this space into subspaces of objects so that the objects located in the subspaces form homogeneous groups.

This work aims to process three-dimensional models by their metadata. 3D models are carriers of complex data that are problematic to analyse and classify. There are two ways to solve the problem: to develop a neural network for scanning a 3D model with clarification of all its features and for comparison with other models, or to develop an algorithm for automatic grouping of 3D model metadata and bring the results of analog output closer to the minimum errors.

Metadata of 3D models is a set of the following standardized information about a file: model name, dimensions, file size, file format, keywords, etc. Metadata can be used to speed up your workflow as well as to organize your files.

The development of an algorithm for automatic grouping of objects, 3D models, based on their metadata, will allow grouping objects according to certain characteristics, contributing to the rapid search for analogues for the selected 3D model automatically, displaying analogues in recommendations. This solution is necessary in private databases of enterprises using additive manufacturing or any enterprises in whose business processes there are subprocesses for processing complex information in the form of 3D models.

Problem Statement

Clustering is the division of a set of objects into subsets (clusters) according to a given criterion. Each cluster includes objects that are as similar as possible to each other (Raskin, 2014). Usually input data can be indicative description of objects or distance matrix. Among the most common applications of clustering are the following: data compression, search for patterns within data, search for anomalies (Kazakovtsev, 2016).

To calculate distances between objects different metrics or distance functions can be used. The most common and well-known metric is the Euclidean distance. Manhattan and Chebyshev distances are other widely used metrics (Kazakovtsev et al. 2019; Shevchenko et al., 2021).

On the other hand, there are number of similarity measures, such as Jaccard similarity or Levenstein distance. The Jaccard coefficient (Makhruse, 2019) measures the similarity between finite sets of samples and is defined as the size of the intersection divided by the size of the union of the sets of samples:

$J\left(A,B\right)=\frac{\left|A\cap B\right|}{\left|A\cup B\right|}=\frac{\left|A\cap B\right|}{\left|A\right|+\left|B\right|-\left|A\cap B\right|}$, (1)

Levenshtein distance is the number of operations required to convert one string to another. The variables a and b represent our two strings, i and j are the character positions in a and b, respectively.

To calculate quality of clustering it is important to take into account the following:

• Compactness: cluster elements should be as close to each other as possible;
• Separability: the distance between different clusters should be as small as possible;
• Concept: cluster elements should be concentrated around the center of the cluster (not for all algorithms).

In the k-means problem it is required to find such k centers of clusters $X_1\dots X_k$ in d-dimensional space, so that the sum of the squared distances from them to the given points $A_i$ ( $A_1\dots A_k$) is minimal.

The algorithm of the same name consistently improves the known solution, allowing finding a local minimum. This is a simple and fast algorithm applicable to the widest class of problems. The algorithm has limitations - at the beginning of the solution, it is necessary to set the number of groups k into which the objects are divided, and the result strongly depends on the initial solution, usually chosen randomly (Wang & Su, 2011).

An algorithm for the k-medoid problem, “Partitioning Around Medoids (PAM)”, was proposed by Leonard Kaufman and Peter J. Rousseeuw (Makhruse, 2019). It is similar to the k-means algorithm: both work based on attempts to minimize error, but PAM works with medoids - objects that are part of the original set and represent the group in which they are included, and k-means works with centroids - artificially created objects that represent cluster. The PAM algorithm divides a set of objects into clusters ( and are the input data of the algorithm) (Dmitriev, 2018). The algorithm works with a distance matrix, its goal is to minimize the distance between the representatives of each cluster and its members.

The well-known k-medoids algorithm is a modification of the classical k-means clustering algorithm and is designed to solve problems of selecting groups of objects (clusters) in cases where objects are clustered without using the properties of a linear space. Such problems arise when a specific measure of the proximity of objects (not distance) is used, for example, when clustering undirected graphs. In this case, unlike k-means, the center of the cluster may not be any point of the feature space (centroid), but only a point belonging to the clustered sample - the medoid.

Research Questions

The following questions were posed during the study:

• How to increase demand for products?
• How to select the analogues of 3D models automatically?
• How to ensure the similarity of chosen analogues?

Purpose of the Study

This project was implemented in the work process of the “MSK” construction company to increase demand for products by improving the quality of selection of analogues of 3D models in the form of recommendations by developing the structure of an algorithm for automatic grouping of 3D model metadata. This is an example of usage of our developments. This implementation allowed the company to improve the quality of selection of offers when working with clients, effectively manage the additive manufacturing process (in case of defects in the model during printing due to improper preparation, it is possible to choose an analogue in view of the urgency to provide the order to the client), reduce labor costs in the process of designing 3D models (when creating a 3D model, the algorithm will allow you to find an analogue of the required model for making changes without spending time creating a model from scratch).

Research Methods

One of the most important aspects in data processing and building a machine learning model is understanding how the data is stored. The first step is to investigate the sources for the storage, processing and distribution of 3D models and collect metadata.

Raw data contains fields, that will have no role in the operation of the grouping model. Thus, our model takes into account the following: file size, model name, number of polygons and vertices, topology, file format, dimensions of the model, keywords.

Number of polygons and vertices

A polygon is a plane in Euclidean space, which has the coordinates "x", "y", "z" - length, height and depth. A polygon has vertices from three to infinity. In 3D modeling programs, it is customary to use 4-sided polygons, so when modeling, you have to ensure that all 4 polygon vertices are in the same or almost the same plane. A polygon with 4 vertices is mathematically very easy to turn into two triangular ones with two common vertices, which is done automatically (Building tables, n.d.).

Polygon modeling is divided into three types: low poly, medium poly and high poly (Corinthian pillar | 3D model, 2021).

Next, it is planned to calculate the distances of each individual word to another and form a matrix of distances, based on which we will calculate the position of the model among the described structure of the keyword parameter. Thus, all the necessary parameters of the metadata of 3D models were normalized and brought to a mathematical form, which allows further analysis, in particular, cluster analysis.

To operate the data, it has to be reduced to “mathematical” form: “file size”, “polygons” and “vertices” will not be changed, “model name” will be represented by its ID (same names have same ID’s), “file format” is described according to Table 1, “dimensions of the model” contains width, length and height, “number of vertices” and “number of polygons” stores integer values.

When modeling in 3D with polygons, it's important to build all your models using quads and triangles. The characteristic "topology" is transformed into a numerical format using a Boolean representation, where 1 is the use of this topology, and 0 is its absence (Cheung, 2003).

After doing all of the above, the data is normalized by scaling between 0 and 1

Next step is to calculate pairwise distance matrix. Figure 1 shows an example of such a matrix in MS Excel for a small dataset of 30 elements taken as an example.

See Full Size >

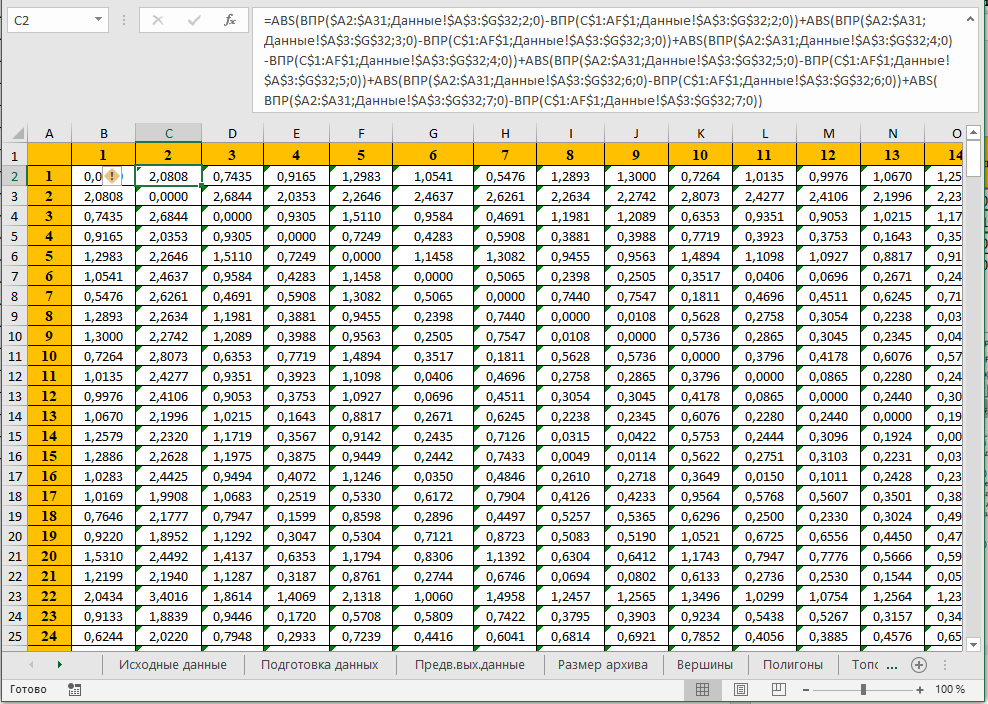
To calculate distances between keywords Jaccard similarity is used.

As a result of the calculations, we obtain two matrices of distances for pairs of models: the distance for 6 parameters is calculated based on the Manhattan distance and the distance for the 7th parameter, keywords, is calculated using the Jaccard coefficient. To merge two distance matrices into one we combine the calculated distance for 6 parameters with the distance for keywords (multiplied by 2 to increase the influence of keywords over other parameters). Thus, the distance between the two models lies in the range [0, 8]. Based on these distances we can clusterize models.

It is possible to find a list of 3D models closest similar in descending order to the selected model, taking into account the calculated distance between pairs of 3D models. The proposed models with the display of their cluster allow us to conclude how large the distance between the models is in the first three orders. Based on this, a decision can be made whether these models should be recommended as an analogue. Let's test the developed algorithm on to evaluate the effectiveness of its work.

Findings

In this chapter, a series of test runs of the algorithm is presented to form a statistical representation of the effectiveness of the algorithm. To achieve this, we compared the obtained probability of similarity of models with an expert assessment on a predetermined sample of metadata objects (initial metadata table). The expert assessment will be normalized on a scale from 1 to 10. The efficiency of the algorithm will be represented by values from 0 to 100. A positive result of the evaluation of the algorithm launch will be the hit of the probability percentage for the selected model for the proposed model. In the range of expert evaluation (a number from 1 to 10, where one is an almost perfect match) * 10 with an error of 10. Accordingly, other results will be an unsuccessful outcome of the algorithm check. The results obtained are presented in Table 2.

As it can be seen, developed system of automatic grouping results mostly coincided expert assumptions.

Conclusion

Implementation of the developed automatic grouping algorithm allows companies that works with 3D models to improve the quality of selection of proposals when working with clients, effectively manage the additive manufacturing process (in case of defects in the model during printing due to improper preparation, it is possible to choose an analogue in view of the urgency to provide an order to the client), reduce labor costs in the design process 3D models (when creating a 3D model, the algorithm will allow you to find an analogue of the required model for making changes without spending time creating a model from scratch). Based on the algorithm, it is possible to create statistics on objects and various indicators, including those related to the presence of a defect, which will allow in the future to look for patterns between objects and consider risks.

The data were conditionally divided into four categories, each of which was normalized.

To calculate the distances between all models, a matrix of distance values was formed for each pair of models taken. To be able to search not only for one model, but also for several models similar in value, a matrix of distance clusters was formed. Such a matrix reflects not distances, but clusters, which include pairs of models. Thus, it is possible to obtain not only the closest model to the selected model, but also to compare the remaining pairs of the found model by the size of the cluster. In view of this, it is possible to determine several models that are predictably similar with a sufficiently high accuracy of models.

After calculating the distances between texts, two matrices of distances of pairs of models were obtained: 6 parameters normalized using the distance of city blocks and the 7^th parameter, keywords normalized using the Jaccard coefficient.

Next, the calculated distances, by 6 parameters, were combined with the distance, by keywords, (multiplied by 2 to increase the influence of keywords over other parameters). The following matrix of distances of pairs of models based on 8 parameters was obtained, since the keywords occupy two positions at once.

After the data was grouped, 300 reference clusters (ranges) were created, to which 3D models may belong. Given that the parameters of 3D models are 8, we conclude that a pair of models can have a maximum distance equal to 8. Based on this equality, clusters of pairs of models are formed according to the degree of distance from each other. This will allow in the future to search for models similar in distance. Thus, a table of clustering distances of pairs of models was formed. A formula for searching for 3D models, the closest similar ones, is compiled, considering the calculation of the minimum distance and the selected model. A function for inferring the cluster to which the recommended model belongs has been developed.

It is possible to find a list of 3D models closest similar in descending order to the selected model based on the calculated distance between pairs of 3D models. The proposed models with the display of their cluster allow us to conclude how large the distance between the models is in the first three orders. Based on this, a decision can be made whether these models should be recommended as an analogue. The algorithm was also tested for the correctness of its operation.

Acknowledgments

This work was supported by the Ministry of Science and Higher Education of the Russian Federation (Grant No. 075-15-2022-1121).

References

• Building tables. (n.d.). Retrieved on 20 October, 2022, from https://www.ibm.com/docs/en/spss-statistics/25.0.0?topic=SSLVMB_25.0.0/spss/tables/idh_idd_table_assign_vars.html

• Cheung, Y. M. (2003). k-Means: A new generalized k-means clustering algorithm. Pattern Recognition Letters, 24(15), 2883-2893.

  Google Scholar

  Crossref

• Corinthian pillar | 3D model. (2021). CGTrader. https://www.cgtrader.com/free-3d-models/architectural/decoration/corinthian-pillar

• Dmitriev, I. N. (2018). Fast k-medoids cluster analysis algorithm. Applied Discrete Mathematics, 39, 116-127.

• Kazakovtsev, L. A. (2016). The method of greedy heuristics for systems of automatic grouping of objects [Doctoral dissertation]. Siberian Federal University.

• Kazakovtsev, L., Stashkov, D., Gudyma, M., & Kazakovtsev, V. (2019). Algorithms with greedy heuristic procedures for mixture probability distribution separation. Yugoslav Journal of Operations Research, 29(1), 51-67.

  Google Scholar

  Crossref

• Makhruse, N. (2019). Modern trends in data mining methods: clustering method. CyberLeninka: scientific electronic library, 6, 1-19.

• Raskin, A. A. (2014). Comparison of techniques for clustering partially ordered sets. Proceedings of the Institute for System Programming RAS, 26(4), 91-98.

• Shevchenko, O., Khakhanov, I., & Khakhanov, V. (2021). Data search and analysis based on the similarity-difference metric. CyberLeninka: scientific electronic library, 1, 51-60.

• Wang, J., & Su, X. (2011). An improved K-Means clustering algorithm. In 2011 IEEE 3rd international conference on communication software and networks (pp. 44-46). IEEE.

  Google Scholar

  Crossref