Abstract
Many real-world global optimization problems are presented by a black-box model, therefore there is no information on properties of the objective function and its derivatives. Differential evolution (DE) is one of search algorithms, which demonstrates the high performance in solving global black-box optimization problems. Usually DE shows good global convergence, but it is slow in the local convergence. A local search can efficiently find a local optimum with high accuracy but cannot identify a basin of the global optimum. In the study we have proposed a hybrid of DE and the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm. In BFGS derivatives are substituted by their approximations using the finite difference method. We have tested 3 different schemes of the cooperation of DE and BFGS. Using a set of benchmark optimization problems, the experimental results have shown that the hybridization can improve the performance of the standard DE algorithm. At the same time the choice of the hybridization scheme affects the results.
Keywords: Global optimization, black-box optimization, differential evolution, quasi-Newton methods, BFGS
Introduction
Many real-world global optimization problems are presented by a black-box model, therefore there is no information on properties of the objective function and its derivatives. In this case different blind search methods, heuristics, and metaheuristics are applied (Zhan et al., 2022). Evolutionary algorithms are one of the most popular and efficient metaheuristics for solving hard optimization problems. Evolutionary algorithms are stochastic and population-based approaches (Del Ser et al., 2019).
Differential evolution (DE) is one of search algorithms, which demonstrates the high performance in solving global black-box optimization problems (Storn & Price, 1997). DE uses the difference-based mutation of random solution vectors and demonstrates the ability of global exploration of the search space. When a basin of the global optima was found, DE converges to the optima using the selection operator (Das & Suganthan, 2011). Because of the stochastic behaviour, DE demonstrates poor local convergence in the basin of attraction. A local search can efficiently find a local optimum with high accuracy but cannot identify a basin of the global optimum. Broyden–Fletcher–Goldfarb–Shanno algorithm (BFGS) is known as one of the fastest local search algorithms (Fletcher, 1987). BFGS is a quasi-Newton method that uses approximation instead of computing the exact Hessian matrix. At the same time BFGS uses first order derivatives, which can be replaced with their numerical estimates.
The performance of evolutionary algorithms can be improved by their hybridization with other methods. One of the most popular approaches is a combination of local and global search algorithms [also known as memetic evolutionary algorithms (Hart et al., 2005; Vakhnin & Sopov, 2020)]. In the study we have proposed a hybrid of DE and the BFGS algorithm.
A cooperation of DE and BFGS in the hybrid can be implemented in different ways:
- using the BFGS method for the final improvement of the best-found solutions, obtained by the DE algorithm,
- using the BFGS method for the intermediate improvement of trial solutions in the main DE’s loop,
- and alternating DE and BFGS methods during the run.
Problem Statement
The problem statement of global black-box optimization can be stated in the following way (1):
,(1)
here is an objective function, , is an -dimensional solution, the search space ( ) is defined by box constrains , and are the lower and upper values.
The solution to the problem (1) is
.(2)
We do not set any requirements for the objective function and don’t use any properties of the objective function and its derivatives in search algorithms. Thus, the objective function is viewed as a black-box model.
Research Questions
In the study we use implementations of DE and BFGS algorithm with pseudocodes presented in Table 1 and 2.
Three hybrids of DE and BFGS mentioned above have been implemented as described below:
- The first algorithm (titled as DE_BFGS 1) performs DE and BFGS consequentially. The best-found solution from the DE run is used as the starting point in the BFGS algorithm for making the final local improvement.
- The second algorithm (DE_BFGS 2) runs the BFGS algorithm after performing crossover (step 4 in Table 1) for each trial solution.
- The third algorithm (DE_BFGS 3) alternates DE and BFGS methods. We apply the BFGS algorithm after every 10 generations of DE. DE continues its evolution with the updated population.
Because of many variants of hybrid implementations, it’s necessary to estimate the performance of them and to choose the best one.
Purpose of the Study
The purpose of the study is the experimental comparison of the proposed ways of hybridization. For making that, it’s necessary to complete software implementation of algorithms, to obtain statistical data on numerical experiments, and to proceed the data for establishing the best hybrid.
Research Methods
In this study, we have compared four different approaches, including the original DE algorithm and three hybrid schemes. All of them were tested on 4 benchmark problems: Ackley, Griewank, Rastrigin, and Rosenbrock functions (Awad et al., 2016).
The number of variables of each problem is equal to 10 and 20. We have used the maximum number of fitness evaluations as the stopping criteria. The maximum number of fitness evaluations is 200000 for problems with 10 variables and 1000000 for problems with 20 variables. All algorithms are evaluated over 40 independent runs. The comparison of algorithms is based on medians of the best-found values and errors. The error measure is used to show the distance from the known global optimum if an algorithm hasn’t reached the minimum of the objective function.
All algorithms in the comparison are implemented using the Python programming language with no external packages. We have used a multi-CPU parallelization for improving the computational performance in our numerical experiments.
Findings
The results of experiments are presented in Tables 3 and 4.
Figures 1-4 shows the variance of the results in the runs using box-plot diagrams. As we can see from figures 1,2,3, and 4, DE_BFGS 1 and DE_BFGS 3 give more stable results. At the same time, DE_BFGS 1 wins 2 of 4 times on hard multimodal problems. The standard DE outperforms hybrids with the Rosenbrock function, this can indicate that BFGS performs not well with ravines.
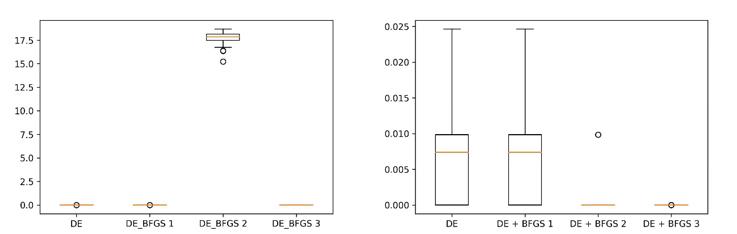
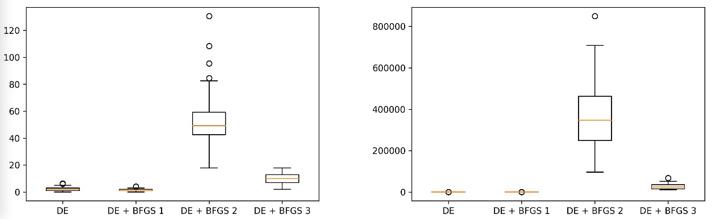
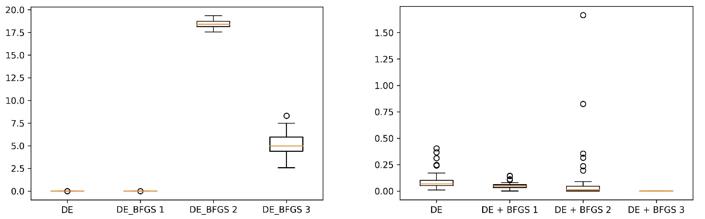
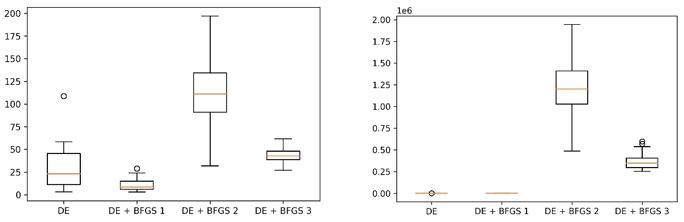
We have also visualized the convergence in one run to demonstrate how algorithms improve the best-found solution. An example on the Rastrigin problem with 10 variables is shown in Figure 5.
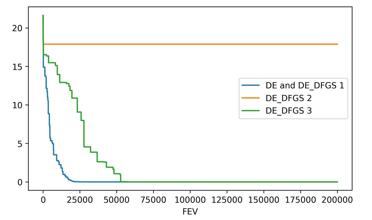
Plots for DE and DE_BFGS 1 are combined, because DE_BFGS 1 doesn’t use BFGS in the main run. As we can see in Figure 5, DE_BFGS 2 uses too greedy search and cannot escape a local optimum. DE_BFGS 3 can be slower than DE, but as we can see from the average results, it outperforms DE.
Conclusion
In the study, we have compared the performance of different schemes of combining global and local search in order to estimate how the hybridization affects the performance of DE. BFGS have been used as a local search in the hybrid. The experimental results have shown that the hybridization improves the performance on hard multimodal problems but yields to the standard DE on the unimodal problem with a ravine.
DE_BFGS 2 has shown the lowest performance, because the intensive local search leads to premature convergence. DE_BFGS 1 has shown that the original DE converges not well in the basin of attraction of the identified optimum, thus the usage of a local search after the run of DE is necessary. DE_BFGS 3 has a potential for improvement, because there are many different options for setting its parameters.
In further work, we will try different ways of implementing DE_BFGS 3, including a self-adaptive scheme. Also, the standard DE can be substituted by more advanced global search algorithms (for example, SaDE or SHADE). Finally, the set of benchmark problems can be extended.
Acknowledgments
This research was funded by the Ministry of Science and Higher Education of the Russian Federation, Grant No. 075-15-2022-1121.
References
Awad, N., Ali, M., Liang, J., Qu, B., & Suganthan, P. (2016). Problem definitions and evaluation criteria for the cec 2017 special sessionand competition on single objective bound constrained real-parameter numerical optimization. Technical Report, Nanyang Technological University, Singapore.
Das, S., & Suganthan, P. N. (2011). Differential Evolution: A Survey of the State-of-the-Art. In IEEE Transactions on Evolutionary Computation, 15(1), 4-31.
Del Ser, J., Osaba, E., Molina, D., Yang, X.-S., Salcedo-Sanz, S., Camacho, D., Das, S., Suganthan, P. N., Coello Coello, C. A., & Herrera, F. (2019). Bio-inspired computation: Where we stand and what’s next. Swarm and Evolutionary Computation, 48, 220-250.
Fletcher, R. (1987). Practical methods of optimization (2nd ed.). John Wiley & Sons.
Hart, W. E., Krasnogor, N., & Smith, J. E. (2005). Memetic Evolutionary Algorithms. In W. E. Hart, J. E. Smith, & N. Krasnogor (Eds.), Recent Advances in Memetic Algorithms. Studies in Fuzziness and Soft Computing (vol. 166, pp. 3-27). Springer.
Storn, R., & Price, K. (1997). Differential Evolution – A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. Journal of Global Optimization, 11, 341-359.
Vakhnin, A., & Sopov, E. (2020). Investigation of the iCC Framework Performance for Solving Constrained LSGO Problems. Algorithms, 13(5).
Zhan, Z.-H., Shi, L., Tan, K. C., & Zhang, J. (2022). A survey on evolutionary computation for complex continuous optimization. Artificial Intelligence Review, 55(1), 59-110.
Copyright information

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License
About this article
Publication Date
27 February 2023
Article Doi
eBook ISBN
978-1-80296-960-3
Publisher
European Publisher
Volume
1
Print ISBN (optional)
-
Edition Number
1st Edition
Pages
1-403
Subjects
Hybrid methods, modeling and optimization, complex systems, mathematical models, data mining, computational intelligence
Cite this article as:
Sopov, A., & Sherstnev, P. (2023). An Investigation of the Hybridization of DE and BFGS Algorithms. In P. Stanimorovic, A. A. Stupina, E. Semenkin, & I. V. Kovalev (Eds.), Hybrid Methods of Modeling and Optimization in Complex Systems, vol 1. European Proceedings of Computers and Technology (pp. 336-342). European Publisher. https://doi.org/10.15405/epct.23021.41

