Abstract
Dynamic multi-objective optimization problems are challenging and currently not-well understood class of optimization problems but it is important since many real-world optimization problems change over time. When changes appear in the problem, there is a necessity to adapt to the changes in such a way that the convergence rate is sufficiently high. The work is devoted to the analysis of the efficiency of Pareto local search algorithms for dynamic multi-objective optimization problems as a method to increase the convergence rate. We propose a hybrid of global and local search algorithms, we use NSGA-2 algorithm as a global optimizer and L-BFGS-B as a local search algorithm. The IEEE CEC2018 benchmark set is used for the experimental comparison of investigated approaches. The experimental results show that the proposed hybridization of NSGA-2 and a local search algorithm can efficiently identify the Pareto front in the case of not intense changes in the environment.
Keywords: Dynamic multi-objective optimization problem, pareto local search, NSGA-2
Introduction
Many real-world optimization problems exist in the dynamic environment and there is a necessity to take into account changes that continuously occurring in the environment. These problems arise in different application areas such as control, engineering and so on.
Dynamic multi-objective optimization is a complex and currently not-well studied class of hard optimization problems. In such problems, objective functions, their parameters and constraints imposed on the search space can change over time (Yazdani, 2021). Objective functions are assumed to be presented by a "black- box" model; therefore, forms of objective functions and their properties remain unknown and are not involved in the optimization process. Also, there is no possibility to evaluate derivatives of objective functions and this fact significantly complicates the choice of a suitable method for solving problems of this class.
Approaches for solving dynamic multi-objective problems (DMOOP) based on evolutionary algorithms (EA) have been presented in many publications. The local search shows the successful results as one of improving mechanisms of EAs for solving static single- and multi-objective optimization problems. The same approach can be implemented for improving DMOOP solutions.
The rest of the paper is organized as follows. Section 2 presents the description of DMOOP. Section 3 contains experimental setups and some general settings. In Section 4, the experimental results are presented. In conclusion, the obtained results are summarized, and some further ideas are suggested.
Problem Statement
Dynamic multi-objective optimization problem
A dynamic multi-objective optimization problem can be defined as follows:
(1)
here denotes a set of objective functions, is the number of objective functions; is a solution vector from the feasible search region ; is a parameter vector of an objective function that changes over the time; is the time interval, in which the problem is considered.
In real-world problems, the vector can contain parameters of the external environment (such as temperature, available resources and so on) that affect the objective function. In the moving peaks benchmark problems this can be a parameter of the peaks’ depth, width, and location. The vector can also include other variable parameters (for example, the number of variables of the objective function) (Azzouz et al., 2017).
DMOOP includes two or more objective functions that must be optimized simultaneously. This means that due to changes in the environment, the Pareto-optimal set (PS) and the Pareto-optimal front (PF) also change. Therefore, within the searching process it is necessary to provide sufficient diversity to be able to efficiently approximate PF of the problem and to fit to appearing changes. This is one of the reasons why EA’s with a population of solutions is an efficient tool for solving DMOOP.
Pareto local search
Local search is used in EAs as a tool, which allows improving the convergence rate of EAs (Sindhya et al., 2008). The main feature of local search algorithms is that the solution changes only in some local area of the search space. Moreover, local search algorithms have proven the convergence to a local optimum.
However, in the case of a multi-objective problem there is the necessity to take into account values of all objective functions. For this purpose, a simple convolution of objective functions or the measure that shows the distance between a referent point (usually the worst point) and obtained PS can be used. Thus, different approaches that use local search (LS) in multi-objective optimization have been proposed as Pareto local search approaches (Chen et al., 2014; Ishibuchi & Murata, 1996; Sindhya et al., 2008). The aim of the Pareto LS algorithm is not to find a single final solution but approximate PF of the problem as accurate as it is possible.
A local search procedure is applied to solutions obtained by EA. For example, Sindhya et al. (2008) proposed Pareto LS approach, which defined as a minimizing procedure of the following objective function:
(2)
here is a reference point; and are maximum and minimum objective values from the population.
As the result, we consider a single-objective optimization problem which can be solved by any known LS method for single-objective optimization.
Research Questions
In this research the following questions were raised:
- Does the use of local search for solving DMOO problems gives an effect?
- Which scheme of hybridization of local and global search is the most effective?
Purpose of the Study
The purpose of this research is to investigate whether the using of LS with EA increases the performance of solving DMOOPs.
Research Methods
Hybridization of local and global search
The hybridization of local and global search can be implemented in different ways. In this research three approaches to the hybridization have been considered:
In these three approaches LS applied to the whole population. However, in the case of the alternation of LS and global search there is a possibility to use only a part of all individuals in LS. This approach allows to perform more steps of LS. In this research, LS uses 10 and 25 solutions from the population with the size equal to 100. Wherein, the number of objective function evaluations is equal in all approaches.
Two different objective functions for applying LS are compared: the function presented in (2) and the negative hypervolume (HV). HV is the accuracy measure in multi-objective optimization that shows the distance between obtained PF and a reference point.
When using LS there is a necessity to set bounds, in which variables of the LS objective function can change. In this research the bounds are computed as follows:
(3)
here is the number of variables in the objective function; is the obtained solution; , is the rate of LS, which is set experimentally in this research. In the case of the low rate, solutions obtained by LS are located not uniformly along PF. An example of the distribution of solutions is shown in Figures 1 and 2.
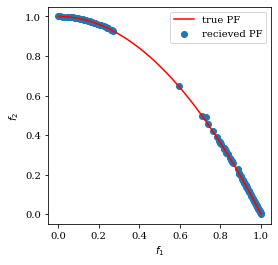
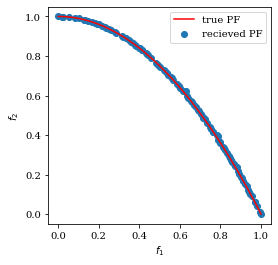
Experimental settings
In this study, the multi-objective optimization algorithm NSGA-2 has been used as a global search method to solve DMOOPs. NSGA-2 is one of well-known methods, its efficiency has been shown in many publications (Deb et al., 2002). DMOOP is considered as a sequence of multi-objective problems on a discrete time interval :
(4)
When a change in the environment occurs, a new population is formed from a half of solutions from the previous population and a half of randomly generated solutions (Rurich et al., 2022).
We use the L-BFGS-B algorithm as LS; in our implementation of L-BFGS-B numerical gradient approximations are used. The IEEE CEC 2018 Dynamic Multi-objective Optimization Benchmark have been used as the test set (Jiang et al., 2018), it contains different types of DMOOPs with different levels of complexity.
IGD (Inverted Generational Distance) and HV are used to evaluate the accuracy of obtained solutions. IGD shows differences between obtained PF and true PF. The DMOOP benchmark uses the averaged measures (denoted as MIGD and MHV):
(5)
here ; is the Euclid distance between the -th element of and the nearest element of ; is the number of time intervals.
(6)
here HV is the hypervolume operator. In the publication (Jiang et al., 2018), there is the recommendation to calculate the reference point as where is the maximum value of the -th objective function in true PF in the -th time moment, is the number of objective functions.
Findings
Table 1 and table 2 contain the experimental results with IGD and HV averaged over 20 independent runs. The highlighted values in the Table are the best IGD value for each problem among considered approaches.
In the Table 1 we can see that in the cases of using NSGA-2 with LS we achieve the results, which outperforms the results of applying stand-alone NSGA-2. The alternation of LS and NSGA-2 and LS before NSGA-2 show the best results. In Table 2, there are the results of using LS with all, with 10, and with 25 individuals. We can see that in the cases when only a part of solutions is used in LS, we obtain the best results.
Conclusion
The results show that using of LS allows to improve the accuracy of solving dynamic multi-objective optimization problems. Implementation of LS applied to a part of the population shows the best results in comparison with the implementation of LS applied to all population. The received result means that the use of the hybridization of local and global search in solving of dynamic multi-objective optimization problems needs more detailed consideration.
The ideas for further researches are follows. Consider other schemas and approaches of the hybridization of local and global search. Investigate the relationship between the number of individuals in LS that is needed to achieve the best result and the rate of changes. Investigate how rate of the local search can be fitted.
Acknowledgments
This research was funded by the Ministry of Science and Higher Education of the Russian Federation, Grant No. 075-15-2022-1121.
References
Azzouz, R., Bechikh, S., & Ben Said, L. (2017). Dynamic Multi-objective Optimization Using Evolutionary Algorithms: A Survey. In S. Bechikh, R. Datta, & A. Gupta (Eds), Recent Advances in Evolutionary Multi-objective Optimization. Adaptation, Learning, and Optimization, (vol 20, pp. 31-70). Springer, Cham.
Chen, B., Zeng, W., Lin, Y., & Zhang, D. (2014). A New Local Search-Based Multiobjective Optimization Algorithm. IEEE Transactions on Evolutionary Computation, 19(1), 50-73.
Deb, K., Pratap, A., Agarwal, S., & Meyarivan, T. (2002). A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Transactions on Evolutionary Computation, 6(2), 182-197.
Ishibuchi, H., & Murata, T. (1996). Multi-objective genetic local search algorithm. IEEE International Conference on Evolutionary Computation – Nagoya, Japan (20-22 May 1996). Proceedings of IEEE International Conference on Evolutionary Computation, 119-124.
Jiang, S., Yang, S., Yao, X., Tan, K. C., Kaiser, M., & Krasnogor, N. (2018). Benchmark Problems for CEC2018 Competition on Dynamic Multiobjective Optimisation. https://www.semanticscholar.org/ paper/Benchmark-Problems-for-CEC2021-Competition-on-Liu-Lin/0afebb7dd4c537d28213bf8e0705caeae6482763
Rurich, M. A., Vakhnin, A. V., & Sopov, E. A. (2022). The comparison of efficiency of the population formation approaches in the dynamic multi-objective optimization problems. Siberian Aerospace Journal, 23(2), 227-240.
Sindhya, K., Deb, K., & Miettinen, K. (2008). A Local Search Based Evolutionary Multi-objective Optimization Approach for Fast and Accurate Convergence. Parallel Problem Solving from Nature - PPSN X, 815-824.
Yazdani, D. (2021). A Survey of Evolutionary Continuous Dynamic Optimization Over Two Decades – Part A. IEEE Transactions on Evolutionary Computation, 25(4), 609-629.
Copyright information

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License
About this article
Publication Date
27 February 2023
Article Doi
eBook ISBN
978-1-80296-960-3
Publisher
European Publisher
Volume
1
Print ISBN (optional)
-
Edition Number
1st Edition
Pages
1-403
Subjects
Hybrid methods, modeling and optimization, complex systems, mathematical models, data mining, computational intelligence
Cite this article as:
Rurich, M., & Sherstnev, P. (2023). A Hybridization of Local and Global Search for Dynamic Multi-Objective Optimization Problem. In P. Stanimorovic, A. A. Stupina, E. Semenkin, & I. V. Kovalev (Eds.), Hybrid Methods of Modeling and Optimization in Complex Systems, vol 1. European Proceedings of Computers and Technology (pp. 321-327). European Publisher. https://doi.org/10.15405/epct.23021.39

