Self-Configuring Evolutionary Algorithms Based Design of Hybrid Interpretable Machine Learning Models

Abstract

The paper describes an approach in which the decision-making process of an artificial neural network is interpreted by a fuzzy logic system. A neural network and a fuzzy system are automatically designed with the use of the self-configuring evolutionary algorithms. Experiments are carried out on classification tasks. As a result, it is shown that the building of a fuzzy system on the inputs and outputs of a neural network allows one to build an interpreted rule base of a smaller size, as if this rule base were built on the data of the original problem. In addition, the accuracy of such a system is comparable to the accuracy of a fuzzy system trained on the original task. As a result, the researcher has a neural network with high accuracy of solving the problem, as well as a fuzzy system explaining the neural network’s decision-making process. The article presents some constructed rule bases and neural networks for interpretation of which they were built.

Keywords: Fuzzy logic classifier, neural network interpretability, self-configuring evolutionary algorithms

Introduction

In last years a lot of attention to the theme of neural networks was paid. However, despite their effectiveness, neural networks have a disadvantage, which is the complexity of interpreting the resulting model. Trained neural network models are often referred to as a «black box». This means that information about how exactly the model makes a decision is not available. But there are also approaches results of which are a «white box» model. In such approaches, information about the internal relations of the model is available to the user. One of such approaches is systems based on fuzzy logic, since such models have a base of products rules that explain the decision-making process. However, models based on fuzzy logic are not always interpretable, because they often contain too many rules which can be very difficult to understand. In this regard, the idea of combining the two approaches to get advantage of each of them is prospective. The resulting system has the possibility of explaining how the neural network converts inputs into outputs, and itself also performs classification with acceptable accuracy.

Problem Statement

The use of non-interpreted machine learning methods is associated with great risks. These risks are primarily associated with a lack of understanding of how exactly the non-interpreted model makes a decision. An analysis of recent publications makes it clear that interest in the problem of interpretability and trust in machine learning is increasing.

Research Questions

In course of the study the following questions were raised:

• How can a fuzzy system be trained to describe the decision-making process of a neural network;
• With what accuracy can a fuzzy system describe a neural network;
• What accuracy on the initial problem will have a fuzzy system trained on the inputs and outputs of a neural network;
• Are the constructed rule bases different if one builds a fuzzy system on the original problem and build it on the inputs and outputs of the neural network.

Purpose of the Study

Supposedly, the answers to the questions above will help achieve this purpose and contribute to the development of interpreted machine learning systems.

Research Methods

Evolutionary neural network

The approach described in (Lipinsky & Semenkin, 2006) is considered below, in which the ANN structure is optimized using the self-configuring genetic programming method (Koza, 1990). ANN is encoded as a binary tree. The functional set consists of two operations: "+" – the operation of combining neurons into layers; ">" – the operation of ordering two structures one after the other. The terminal set contains inputs and hidden neurons with various activation functions. So, for a problem with 4 input variables, the terminal set may look like this: T = {in1, in2, in3, in4, 2rl, 2gs, 2sg, 2tg}. Where the number means the number of hidden neurons in the block, and the two symbols are the name of the activation function. So, "2sg" is a block with two hidden neurons with a logistic (sigma) activation function. Elements in1, in2, etc., are blocks of input neurons.

Using this method, it is possible to encode the network structure in the form of a process of constructing this structure from elementary parts of the network (neurons or groups of neurons). Figure 1 shows an example of encoding the ANN structure in a binary tree.

See Full Size >

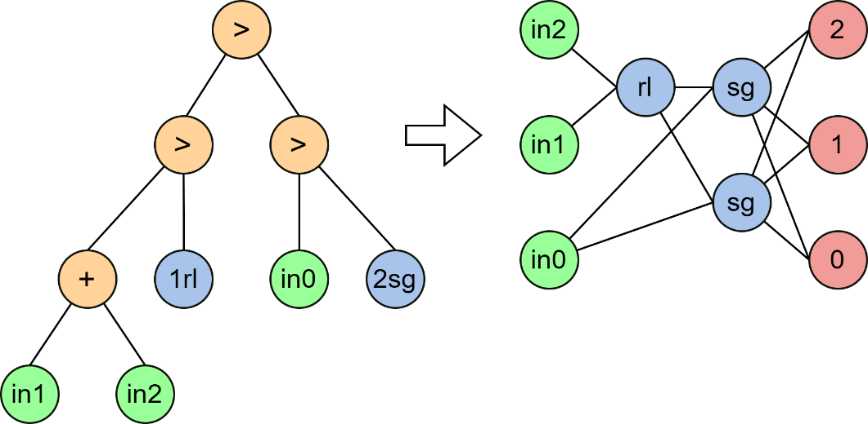
It can be noted that with the help of such coding, structures of varying complexity can be encoded: connections can pass not only from layer to layer; various activation functions in the same network; incompletely connected connections, etc.

The fitness function of the genetic programming algorithm forming the ANN is equal to the efficiency of the network on the problem being solved after learning its weighting coefficients. The tuning of the weight coefficients of such ANNs can be carried out by an evolutionary optimization algorithm (EA). In this paper, a self-configured genetic algorithm is used (Semenkina, 2013).

Findings

Since evolutionary optimization algorithms are stochastic procedures, the results obtained with their help are random. Therefore, the models were tested according to the scheme of multiple runs with 5 block cross-validation. As an estimation of the accuracy of the generated models (ANN and FLC), the percentage of correctly classified objects was used.

At the first stage, the ANN is automatically designed using self-configuring EA. Further, the ANN inputs and the obtained outputs are passed for automatic FLC construction. The accuracy of the FLC is defined as the number of matching outputs of the ANN and FLC. Having an FLC model trained on the ANN inputs and outputs, it is possible to evaluate its accuracy for the classification problem being solved. To do this, the FLC model gets inputs from the original dataset and the accuracy is estimated as the relative number of matching class labels from the dataset and FLC outputs.

Below, Table 1 shows the average accuracy of the obtained models for each classification task. For simplicity of perception, we introduce the following enumeration: 1 – the accuracy of the ANN on the classification problem; 2 – the accuracy of the FLC on the classification problem; 3 – the accuracy of the FLC on the inputs and outputs of the ANN; 4 – The accuracy of the FLC on the original classification problem.

Table 1 shows that FLC solves the classification problems under consideration worse (columns 1 and 2). The accuracy of ANN modeling using FLC is relatively high for all tasks except the last one (column 3). It can be noted that the accuracy of FLCs trained on the inputs and outputs of ANN is comparable to the accuracy trained by FLC on the original classification problem.

During the analysis of the results, it was noticed that the average number of prerequisites for approach 4 is much lower than for approach 2. For comparison, on the BCW task, the average number of prerequisites decreased from 15.98 to 8.15. As an example, consider the rule base for the BCW task:

if (mean radius is) and (mean texture is) and (mean perimeter is) and (mean area is) and (mean compactness is) and (mean concavity is) and (mean concave points is) and (mean symmetry is) and (radius error is) and (texture error is) and (compactness error is) and (concavity error is) and (concave points error is) and (symmetry error is) and (worst radius is) and (worst smoothness is) and (worst compactness is) and (worst concave points is) and (worst symmetry is) then Malignant

if (mean radius is) and (mean perimeter is) and (mean area is) and (mean compactness is) and (mean concavity is) and (mean symmetry is) and (mean fractal dimension is) and (radius error is) and (area error is) and (compactness error is) and (concave points error is) and (fractal dimension error is) and (worst texture is) and (worst area is) and (worst concavity is) and (worst concave points is) then Benign.

That is, the rule base includes only two rules, but the number of prerequisites in each of them is more than 15. Thus, despite the fact that the FLC algorithm returns rules that are understandable, in principle, to a person, the size of these rules does not allow to be easily interpreted.

At the same time, the rules based on the ANN inputs and outputs have a much smaller size, which contributes to their interpretation. To demonstrate this, table 2 presents the rule based obtained for the models whose effectiveness is presented in Table 1.

Additionally, let's consider the ANN structure constructed for the BCW problem. In figure 2, input neurons are marked in green, hidden neurons are shown in blue, and network outputs are shown in red. Hidden layers that have no input connections work as bias neurons and return 1.

See Full Size >

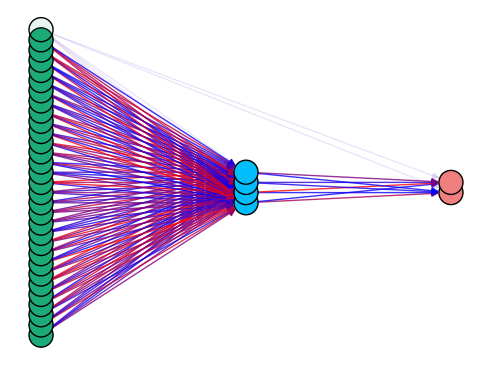
Although this ANN has a relatively small structure, it is difficult to determine how ANN converts input data into output. However, using FLC, it is possible to describe the ANN decision-making process. So, table 2 shows the rule base for the BCW task, consisting of only 2 rules, according to which it is easy to understand how does ANN from Figure 1 work.

table 2 shows that for most tasks the number of rules does not exceed the number of classes and the number of prerequisites in the rules varies from 1 to 4. Moreover, not all input variables are used to build rules. Thus, the rule base built on the inputs and outputs of the network has a much smaller size compared to the base built on the original data set with comparable classification accuracy.

Conclusion

This paper demonstrates the effectiveness of an approach that allows automatic designing simple and interpretable data mining models for classification problems using self-configuring evolutionary optimization algorithms. This approach consists in the fact that with the help of a self- configuring EA, an ANN is automatically designed that solves the classification problem with the required accuracy, then also with the help of EA, an FLC is automatically designed that interprets the results given by this ANN. At the same time, this FLC has comparable effectiveness, i.e. also sufficient accuracy and is based on a small number of simple rules. This distinguishes it from FLC, designed using the same approach based on self-configurable EA, which (FLC) turns out to be non-interpretable.

Acknowledgments

This work was supported by the Ministry of Science and Higher Education of the Russian Federation (Grant № 075-15-2022-1121).

References

• Cordon, O., Herrera, F., Gomide, F., Hoffmann, F., & Magdalena, L. (2001). Ten years of genetic fuzzy systems: current framework and new trends. Proceedings Joint 9th IFSA World Congress and 20th NAFIPS International Conference, 3, 1242-1246.

  Google Scholar

  Crossref

• Credit risk. Kaggle. (2022). Credit risk. Will the Customer pay the financing or not? https://www.kaggle.com/upadorprofzs/credit-risk

• Dua, D., & Graff, C. (2019). UCI Machine Learning Repository. https://archive.ics.uci.edu/ml/datasets/banknote+authentication

• Ishibuchi, H., Nakashima, T., & Murata, T. (1999). Performance evaluation of fuzzy classifier systems for multidimensional pattern classification problems. IEEE Trans. on Systems, Man, and Cybernetics, 29, 601-618.

  Google Scholar

  Crossref

• Kahraman, H. T., Sagiroglu, S., & Colak, I. (2013). Developing intuitive knowledge classifier and modeling of users' domain dependent data in web. Knowledge Based Systems, 37, 283-295.

  Google Scholar

  Crossref

• Koza, J. (1990). Genetic programming: a paradigm for genetically breeding populations of computer programs to solve problems. Stanford University.

• Lipinsky, L., & Semenkin, E. (2006). Primenenie algoritma geneticheskogo programmirovaniya v zadachah avtomatizacii proektirovaniya intellektual'nyh informacionnyh tekhnologij [Application of the genetic programming algorithm in the tasks of design automation of intelligent information technologies]. Bulletin of the Siberian State Aerospace University, 3(10), 22-26.

• Semenkina, M. E. (2013). Samoadaptivnye evolyucionnye algoritmy proektirovaniya informacionnyh tekhnologij intellektual'nogo analiza dannyh [Self-adaptive evolutionary algorithms for designing information technologies for data mining]. Artificial intelligence and decision-making, 1, 12-24. [in Rus.].

• Street, W. N., Wolberg, W. H., & Mangasarian, O. L. (1993). Nuclear feature extraction for breast tumor diagnosis. IS&T/SPIE 1993 International Symposium on Electronic Imaging: Science and Technology, 1905, 861-870.

  Google Scholar

  Crossref

• Yeh, I.-C., Yang, K.-J., & Ting, T.-M. (2009). Knowledge discovery on RFM model using Bernoulli sequence. Expert Systems with Applications, 36(3), 5866-5871.

  Google Scholar

  Crossref