Artificial Neural Network Architecture Tuning Algorithm

Abstract

In this paper, we will consider artificial neural networks, one of the most powerful methods of data analysis. For each individual task, the type of neural network changes, and its various parameters are selected, which takes too much time and resources. To avoid these shortcomings, a self-tuning algorithm for the architecture of the neural network was developed and implemented, due to the genetic algorithm. An artificial neural network has been implemented for data classification tasks. This implementation provides the ability to select the number of hidden layers in the artificial neural network, the number of neurons on each of the layers, the type of activation functions for each neuron of the network. Nfr of the implementation of this evolutionary algorithm is the different lengths of individuals in the population and the ability to manipulate it. A genetic algorithm has been implemented that allows coding all the parameters of the neural network discussed above. The algorithm was developed using the modern Keras neural network training library. The efficiency of the developed algorithms was compared with each other.

Keywords: Optimization, artificial multilayer neural networks, genetic algorithm, classification, Keras

Introduction

As described by Rutkovskaya et al. (2006) and Aksenov and Novoseltsev (2006), to solve problems using an ANN, the user sets its structure, namely, selects the number of hidden layers and determines the number of neurons on each of them, as well as the types of activation functions. Then, using various methods, the network is trained, some of these methods are described in Sozykin's (2017) article. If the user is satisfied with the efficiency of work, the resulting model is subsequently used to solve the problem, otherwise the structure is changed and the procedure is repeated again.

In this paper, an algorithm for tuning the NN architecture was proposed using evolutionary algorithms. Evolutionary algorithms are a direction in artificial intelligence that uses and models the processes of natural selection, describes Emelyanov et al. (2003). Evolutionary algorithms are not used to study biological populations, but to solve optimization and decision problems.

In the late 1960s, the American researcher John Holland proposed using methods and models of the mechanism of development of organisms on Earth as the principles of combined enumeration of options for solving optimization problems, describe Gladkov et al. (2006). Voronovsky and Makhotilo (1997) writes that Holland proposed a classical genetic algorithm (CGA), in which the fitness of an individual is expressed by some monotonic function of the value of the objective function of the problem. The higher the fitness function, the higher its fitness. In this paper, the genetic algorithm will be considered.

The modern ANN learning library Keras is also used in the work. Implemented in Python and running on top of Theano or Tensorflow. It is designed to be modular, fast, and easy to use, as the author of the library, Francois Chollet (2017), points out in his book. He currently works as an engineer at Google.

Problem Statement

Neural networks need to select the optimal architecture. Typically, the choice of architecture is made by enumeration, various types of them are tested, then, using certain methods, various elements of this architecture are either added or excluded. This is repeated until the neural network is trained.

This approach has a drawback: a lot of resources and time are spent on the selection of architecture and parameters.

Research Questions

To solve the problems described above, an algorithm for tuning the NN architecture was proposed, taking into account modern deep ANN learning libraries.

The efficiency of the implemented algorithm on a representative set of test problems is studied.

Purpose of the Study

Using the algorithms described above and describing the main problem, the purpose of this work was to increase the efficiency of searching for artificial neural network architectures.

Research Methods

The general scheme of the ANN architecture tuning developed algorithm is shown in Figure 1, based on the GA scheme, described by Tsoi and Spitsyn (2006):

See Full Size >

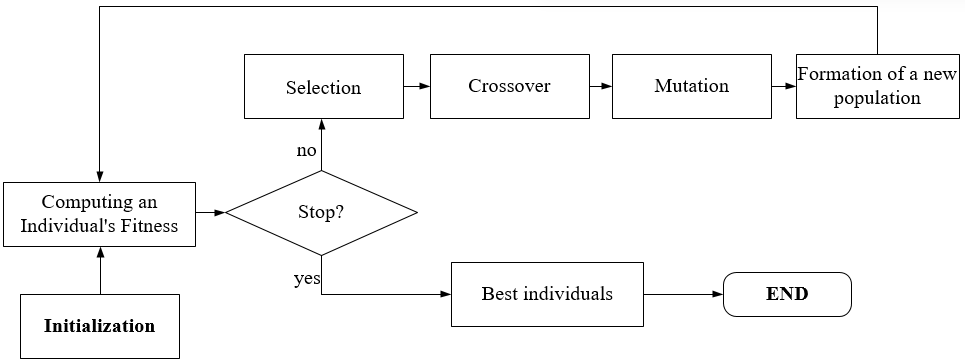
In chromosomes, genes are represented by real values and encode the following neural network parameters:

• α – learning rate;
• β – impulse;
• the number of hidden layers;
• the number of neurons in each layer of the NN;
• type of activation function.

At the initialization stage, the value of α, β is randomly generated, (from 0.01 to 0.1) and (from 0.1 to 0.99), respectively. One hidden layer, the number of neurons is random and does not exceed 10. The type of activation function is chosen randomly.

Below is an example of encoding NN parameters (Figure 2) into a chromosome (Figure 3).

See Full Size >

See Full Size >

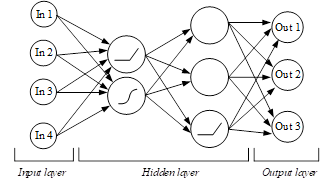
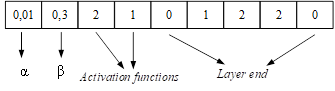
Here is an NN with two hidden layers, the first of which has two neurons, the second has three neurons, with different activation functions. These functions are encoded into the chromosome as follows:

• sigmoid is encoded as 1;
• «ReLu» is encoded as 2.

Zero, in the sequence of genes, marks the end of the layer in the NN.

After initialization, chromosomes are decoded into neural network parameters to calculate fitness for each individual. In this paper, the fitness function is the cross entropy.

Next comes the tournament selection for the selection of individuals for subsequent crossover. Crossover is performed single-point.

A splitting is made between the genes of two parental chromosomes in a random place and these chromosomes are exchanged. It should be noted that when crossing strings of different lengths, the break point of the larger chromosome does not jump out beyond the length of the smaller chromosome. If, when connecting chromosomes, the genes responsible for the end of the layer are nearby, the value "0" is deleted.

Аfter obtaining offspring, the average variant of the mutation is applied. With a certain probability, the value of the activation function encoded in the chromosome changes to the opposite value.

In the genes encoding α and β, with a certain probability, depending on the length of the chromosome, new real values are generated according to the normal distribution law and added to the previous values. If the resulting values are outside their limits, then that value is halved.

After the mutation, all resulting offspring of the population are tested for suitability. Next, a new generation is formed, consisting of the best individual in all generations and the remaining offspring of the population.

Using the same genetic algorithm operators, the encoding method has been modified to work with the Keras library. It allows to train a neural network with a large number of customizable parameters:

• optimizer, for example: Stochastic Gradient Descent (SGD), Adam Optimizer, Adadelta Optimizer;
• loss is the number that the model should minimize during training (Binary Crossentropy, Categorical Crossentropy);
• activation function (ReLu, sigmoid).

Using Keras, the chromosome will look like this (Figure 4).

See Full Size >

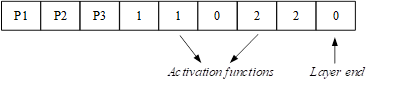
In chromosomes, genes are represented by real values ​​and encode the following neural network parameters:

• P1 – Optimizer type
• P2 – Learning rate
• P3 – Training parameters (momentum - in the case of SGD, β - Adam optimizer).

During initialization, the optimization parameter is chosen randomly between Adam and SGD. The value of P2, P3 is randomly generated from 0.1 to 0.99.

Here, one-point crossover is applied. Since it is not possible in Keras to apply different activation functions in one layer, in case of hitting several different activation functions in one layer, healing is applied. The algorithm detects which of these features prevails in the neural network layer, and replaces the differing values with itself. An example is shown in Figure 5.

See Full Size >

With a mutation, the value of P1 (optimization parameter), with a probability of 50%, can change to the opposite. The values P1 and P2 mutate according to the same rule as α and β described above.

Findings

The efficiency of the algorithms considered in this paper was tested on test problems The efficiency of the algorithms considered in this paper was tested on test problems. Taken from Alcalá-Fdez et al. (2009) KEEL and Asuncion and Newman (2007) UCI machine learning repositories.

For the genetic algorithm and the Keras library, the following parameters are specified:

• number of epochs of the Keras neural network is set to be small - 10 training epochs;
• number of GA generations – 44;
• the number of individuals in the population - 10.

There are various symbols in the table, meaning the following:

• ‘S’ and ‘R’ are activation functions, “sigmoid” and “relu” respectively;
• n.l. is the number of layers;
• n.n. is the number of neurons;
• SGD - stochastic gradient descent;
• Adam optimizer.

The values of accuracies and architectures for each of the samples at different stages of training are given (Tables 1).

The keras_visualizer library was used to visualize artificial neural network architectures. As an example, the problem of classification "Phoneme" is considered. Figure 6 shows the architecture of an artificial neural network obtained on the 44th generation of the neural network.

See Full Size >

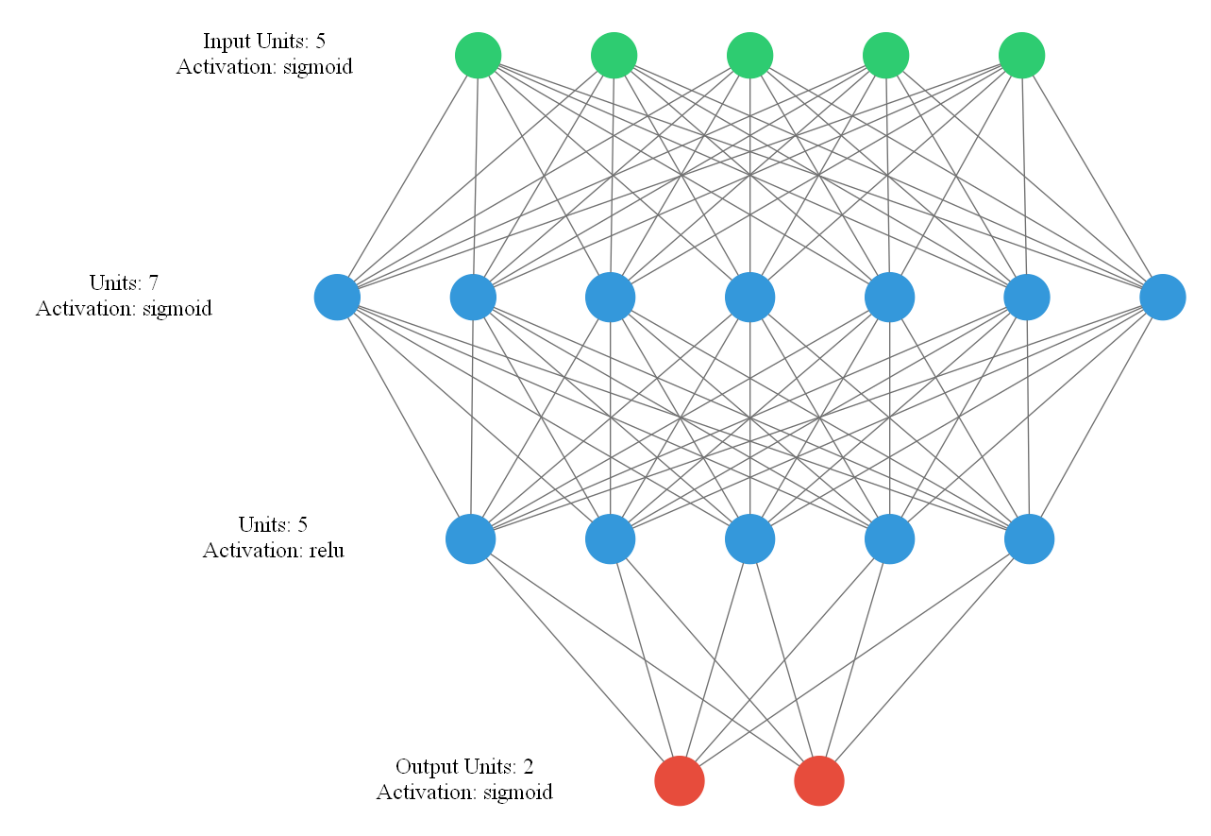
The accuracy of the considered algorithms was compared. Parameters are shown in the Table 2.

The obtained results of the accuracy of the work of neural networks are comparable with other learning algorithms. Table 3 shows the best accuracy values.

It follows from the comparisons that the neural network architecture tuning algorithm performed very well. In the case of the «Ionosphere», «Titanic», «Phoneme» data, the implemented error backpropagation algorithm showed the best result only after searching for suboptimal values of α, β for a specific task, and also required to set the number of hidden layers, neurons in it and learning epochs. And for the architecture tuning algorithm, it was necessary to specify only the number of individuals in the population and the number of generations.

Conclusion

In this paper, a neural network architecture tuning algorithm was developed and implemented. This algorithm for the better differs from other learning algorithms in that, despite the small number of epochs of the Keras neural network, it shows great accuracy results. And even, at the 22nd generation of training, the developed algorithm performed better than the backpropagation algorithm at 60 generations.

All data are successfully classified by the neural network even with a small value of the population of the genetic algorithm. It should be noted that the developed algorithm tends to shallow the neural network, i.e. reduce the number of hidden layers and set neurons for one or two hidden layers.

In the future, the developed algorithm is planned to be modified for convolutional neural networks. Also, the algorithm is planned to be changed to be able to manipulate activation and loss functions.

Acknowledgments

This research was funded by the Ministry of Science and Higher Education of the Russian Federation, Grant No. 075-15-2022-1121.

References

• Aksenov, S. V., & Novoseltsev, V. B. (2006). Organization and use of neural networks (methods and technologies). NTL Publishing House.

• Alcalá-Fdez, J., Sánchez, L., Garcia, S., Jesus, M. J., Ventura, S., Garrell, J. M., Otero, J., Romero, C., Bacardit, J., Rivas, V. M., Fernández, J. C., & Herrera, F. (2009). KEEL: A software tool to assess evolutionary algorithms for data mining problems. Soft Computing, 13(3), 307-318. DOI:

  Google Scholar

  Crossref

• Asuncion, A., & Newman, D. (2007). UCI machine learning repository. University of California, Irvine, School of Information and Computer Sciences. http://www.ics.uci.edu/~mlearn/MLRepository.html

• Chollet, F. (2017). Deep Learning with Python. Deep Learning with Python. Manning Publications.

• Emelyanov, V. V., Kureichik, V. V., & Kureichik, V. M. (2003). Theory and practice of evolutionary modeling: scientific publication. FIZMATLIT.

• Gladkov, L. A., Kureichik, V. V., & Kureichik, V. M. (2006). Genetic algorithms: Textbook (2nd ed.). Fizmatlit.

• Rutkovskaya, D., Rutkowski, L., & Pilinski, M. (2006). Neural networks, genetic algorithms and fuzzy systems. (I. D. Rudinsky, trans.; 2nd ed.) Hotline - Telecom.

• Sozykin, A. V. (2017). Review of learning methods for deep neural networks. Vestn. SUSU. Ser. Calc. math. inform., 6(3), 28-59.

• Tsoi, Y. R., & Spitsyn, V. G. (2006). Genetic algorithm. Representation of knowledge in information systems: a tutorial. TPU Publishing House.

• Voronovsky, G. K., & Makhotilo, K. (1997). Genetic algorithms, artificial neural networks and problems of virtual reality: monograph. OSNOVA.