Classification Algorithm With Lexicase Selection

Abstract

The hybrid fuzzy genetic based algorithm was implemented. The genetic fuzzy systems are applied for classifier learning, and although they allow creating interpretable rule bases, the process of designing a rule base can be improved with specific genetic operators, such as lexicase selection. The influence of lexicase selection on the efficiency of its work for data classification is examined in this article. “Ring”, “Phoneme” and “Satimage” datasets were used for verification. The results were analyzed by verification using Mann-Whitney U test. According to the results of basic hybrid fuzzy genetic based algorithm with lexicase selection of several runs, where in each the duration of the search for the best rule base was limited to five hundred generations, efficiency was only on number of rules, but paired with the previously developed initialization modification, the accuracy and F-score were improved on “Satimage” dataset and the number of rules decreased on all of the datasets.

Keywords: Fuzzy system, genetic algorithm, lexicase selection

Introduction

One of the most popular methods for classifying data is neural networks. There is a significant disadvantage of neural networks that they have poor interpretability: it is difficult for the user to understand why a neural network makes a particular decision. Therefore, researchers have been trying to create hybrid classification systems in which there can be used a combination of various methods, including fuzzy logic. The use of such hybrid systems makes it possible to present the solution of the classification problem in the form of a set of interpreted (user-friendly) logical rules. In addition, the task of obtaining informative features can be combined with the task of minimising feature space thanks to the use of genetic algorithms. Genetic algorithms are adaptive methods for solving optimization problems. They are used to solve a wide range of problems in data analysis, optimization, classification, regression dependencies, and etc (Derigs et al., 1999). A genetic fuzzy system is a fuzzy system that is built using a genetic algorithm which allows finding a suboptimal rule base. There are three stages of the genetic algorithm.

The results depend on which combination of types of selection, crossover and mutation we used. In this paper we will focus on selection. We will check a new method of selecting individuals which is called lexicase selection (Helmuth et al., 2015). Lexicase selection was developed by Lee Spector and Thomas Helmuth for solving program synthesis problems.

Problem Statement

One of the problems is finding the optimal rule base to classify data qualitatively. Therefore, determining and searching for the most effective configuration for the selection of a fuzzy rule base is an urgent task (Stanovov et al., 2014). In this regard, there is a need to check the combination of operators to identify the most effective one, which will reduce the search time and improve the quality of classification.

Research Questions

The article raises the question of the effectiveness of lexicase selection in the algorithm described in (Ishibuchi et al., 2012) and the modified algorithm described in (Pleshkova & Stanovov, 2022). It is necessary to implement lexicase selection that was developed by Lee Spektor and Thomas Helmuth for solving program synthesis problems. The difference between lexicase selection and fitness-based selection is that the algorithm selects parents by considering the performance on individual data points in random order instead of using the fitness function (Helmuth et al., 2015).

Purpose of the Study

Based on the fact that the difference between lexicase selection is in the selecting parents, the main purpose of the study is to determine the influence of lexicase selection on the quality of search and the ability to find the best rule base in a limited time. To do so, it is necessary to compare the implemented algorithm and obtained results.

Research Methods

Fuzzy logic

Fuzzy logic allows us to use not only 1 or 0, but also intermediate values between them. This means that conclusions based on fuzzy logic can be described by a variety of variables: yes, probably not, no, not at all, I can't say, and so on (Rutkovskaya et al., 2004).

To implement fuzzy logic, the first step is to define linguistic variables and create a fuzzy rule in order to then use them, the concept of which will be explained below. Each rule is designed using linguistic terms $L_1,L_2,\dots ,L_{14}$. In the paper (Ishibuchi et al., 2012) they use several fuzzy granulations for each linguistic variable. There are 14 linguistic variables and a “don’t care” condition (DC), which means that for this variable in this rule there is no difference in what value the variable has. Figure 1 shows this concept. We used the same concept in our paper.

See Full Size >

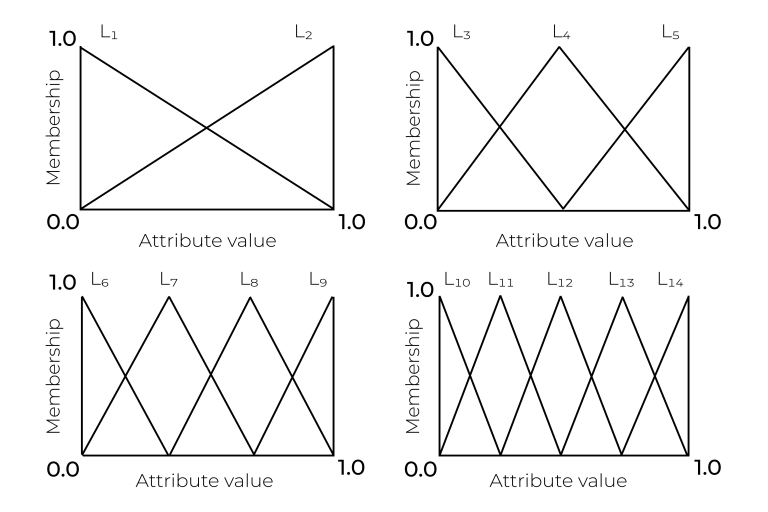
A fuzzy rule consists of a condition of the type “if... then..." with fuzzy terms in the “if..." part and the corresponding class number in the “then..." part (Ishibuchi et al., 1995).

$Rule{R}_q:if{x}_{\mathrm{1}}is{L}_{q\mathrm{1}}\wedge ...\wedge x_{v}is{L}_{qv}thenClass{C}_{q}with{CF}_q,$ (1)

where – number of rules in the rule base, – number of variables in the data sample, – this is a linguistic term, – class label, – rule weight (which is a real number in the unit interval [0, 1]).

A set of rules for the rule base is formed from the rules, the use of which allows us to determine which class an object belongs to by its parameters. In order to form a rule base, we can collect knowledge from experts or use genetic algorithms for the search for the most suboptimal rule base.

Genetic algorithm

The search for a solution in the genetic algorithm includes several components, which is shown in Figure 2.

See Full Size >

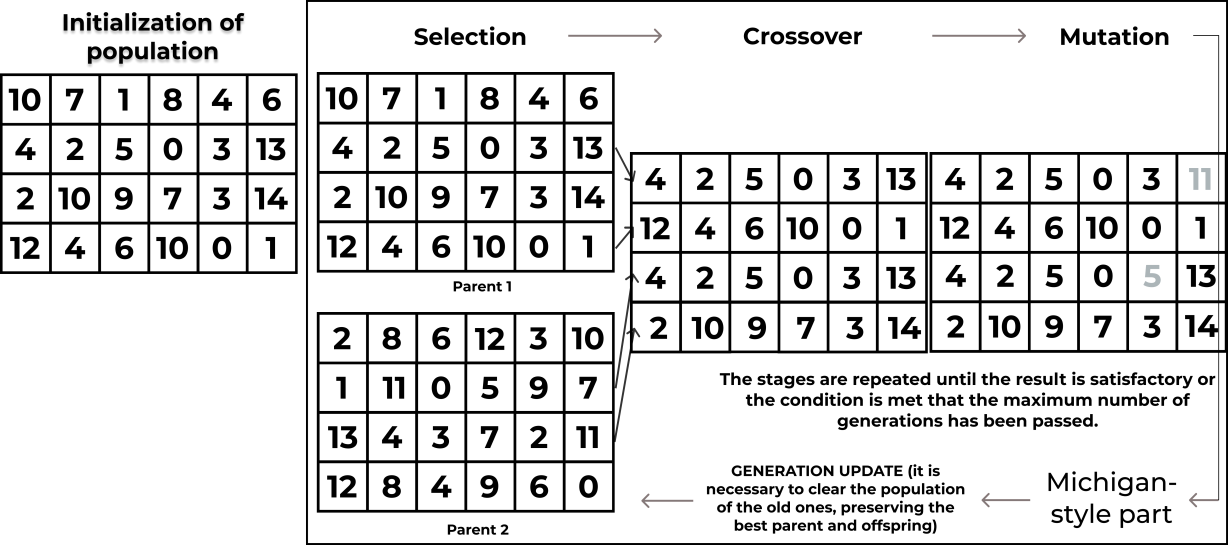
The initial population is presented as a set of possible solutions to the problem and is formed randomly. The work of the genetic algorithm is a set of iterations that will be performed until some stopping criterion is met or the maximum number of generations is reached (Goldberg, 1989). It is important to understand that when designing a genetic algorithm, it is necessary to select its optimal settings. An unsuccessful choice of parameters for a specific task can significantly reduce the efficiency of the genetic algorithm. This leads to serious difficulties in expanding the possibility of using evolutionary algorithms. Therefore, we decided to check how the use of lexicase selection will affect the accuracy of the data classification algorithm (Pleshkova & Stanovov, 2022).

Findings

Testing of the basic and the modified algorithms with lexicase selection was carried out on three tasks taken from the UCI repository (Asuncion, 2007). The characteristics of the data are described in Table 1. The algorithm was run with the number of individuals set to 100. We used three tasks and 500 generations. The 10-fold cross-validation procedure was iterated three times using different data partitions into ten subsets. Average results over 30 runs are summarised in Table 2 for the basic algorithm; in Table 3 for algorithm with lexicase selection (BALS); in Table 4 for algorithm with lexicase selection with initialization modification (MALS).

Table 5 and Table 6 show the results of a statistical test (RST), where the symbol “=” shows that differences are insignificant, the symbol “+” shows that differences are significant and the modification is more efficient and “–” means that differences are significant and the modification is worse than the original algorithm.

Based on the results, we can conclude that a basic algorithm with lexicase selection showed results for accuracy and F-score worse than the original algorithm, but worked better on a number of rules. From Table 6 we can see that “Phoneme” dataset showed improvements on all three parameters, whereas “Ring” and “Satimage” only on number of rules.

We also checked the results with popular methods for classification: Decision Tree (DT), Support Vector Machine (SVM), Logistic Regression (LR), Neural Networks (NN). These methods were taken from sklearn library, the standard parameters were used. The accuracy is presented in Table 7.

Conclusion

Based on the analysis of the results of the lexicase selection method, we conclude that in some cases implemented methods works better paired with modified initialization method which was introduced in (Pleshkova & Stanovov, 2022). Results showed improvements on three datasets with a decreasing number of rules. The results of alternative approaches for data classification showed that our implementation has comparable classification quality to other known methods, and has a better accuracy in some cases. It is necessary to continue the research and implement, for instance, a self-configuring genetic programming algorithm in order to automate the selection of the algorithm’s parameters. To further investigate performance of the implemented method, more tests must be conducted on various datasets with different parameters.

Acknowledgments

This research was funded by the Ministry of Science and Higher Education of the Russian Federation, Grant No. 075-15-2022-1121.

References

• Asuncion, A. U. (2007). UCI Machine Learning Repository. University of California, Irvine, School of Information and Computer Sciences.

• Derigs, U., Kabath, M., & Zils, M. (1999). Adaptive Genetic Algorithms: A Methodology for Dynamic Autoconfiguration of Genetic Search Algorithms. Meta-Heuristics: Advances and Trends in Local Search Paradigms for Optimization (pp. 231-248). Springer. DOI:

  Google Scholar

  Crossref

• Goldberg, D. (1989). Genetic Algorithms in Search, Optimization and Machine Learning. Addison-Wesley Professional.

• Helmuth, T., Pantridge, E., & Spector, L. (2019, July). Lexicase selection of specialists. In Proceedings of the Genetic and Evolutionary Computation Conference (pp. 1030-1038). DOI:

  Google Scholar

  Crossref

• Helmuth, T., Spector, L., & Matheson, J. (2015). Solving Uncompromising Problems With Lexicase Selection. IEEE Transactions on Evolutionary Computation, 19(5), 630-643. DOI:

  Google Scholar

  Crossref

• Ishibuchi, H., Mihara, S., & Nojima, Y. (2012). Parallel Distributed Hybrid Fuzzy GBML Models With Rule Set Migration and Training Data Rotation. IEEE Transactions on Fuzzy Systems, 21(2), 355-368. DOI:

  Google Scholar

  Crossref

• Ishibuchi, H., Nozaki, K., Yamamoto, N., & Tanaka, H. (1995). Selecting fuzzy if-then rules for classification problems using genetic algorithms. IEEE Transactions on Fuzzy Systems, 3(3), 260-270. DOI:

  Google Scholar

  Crossref

• Pleshkova, T., & Stanovov, V. (2022). Hybrid Fuzzy Classification Algorithm with Modifed Initialization and Crossover. In Proceedings of the 14th International Joint Conference on Computational Intelligence – FCTA.

• Pleshkova, T., & Stanovov, V. (2022). Hybrid Fuzzy Classification Algorithm with Modifed Initialization and Crossover. Proceedings of the 14th International Joint Conference on Computational Intelligence. DOI:

  Google Scholar

  Crossref

• Rutkovskaya, D., Pilinsky, M., & Rutkovsky, L. (2004). Nejronnye seti, geneticheskie algoritmy i nechetkie sistemy [Neural networks, genetic algorithms and fuzzy systems]. Hotline-Telecom.

• Stanovov, V. V., Semenkin, E. S., & Begitskiy, S. S. (2014). Hybrid evolutionary algorithm for the formation of fuzzy rule bases for the classification problem. In Proceedings of the III All-Russian Scientific Conference with International participation. Theory and Practice of System Analysis, 2.