Hierarchical Co-Evolution of Self-Configuring Bio-Inspired Algorithms for Production Scheduling With Priorities

Abstract

This article is focused on the consideration of universal formulations of the scheduling problem, which can be used in the broadest sense for any existing production model. The model must have some external parameters for control, but inside it can contain any aspects and moments that are difficult to formalize, for example, dynamically appearing operations, merging and splitting batches, not a fixed order of operations, accumulating a certain weight to start an operation, and anything else. Four universal scheduling problem statements for operational production planning are considered: permutation of the lots processing order, permutation of operation priorities, real operation priorities, and lot order with machine tool priorities nested problem. The second goal of this paper is to suggest a universal optimization approach for solving such problems. A cooperative co-evolutionary method based on self-configuring bio-inspired algorithms for combinatorial and/or real optimization is proposed. For lot order with machine tool priorities problem a hierarchical co-evolution method with both combinatorial and real optimization is proposed. This optimization method helps not only to adjust the parameters of the algorithm in the process of solving the problem but also to eliminate the need to choose an algorithm suitable for a particular problem. That is, a fully automatic adjustment of the optimization method to the optimization problem is achieved, that simplifies the use of intelligent technologies in practice. The effectiveness of the application of this approach to the scheduling problem is shown.

Keywords: Bio-inspired algorithms, self-configuring, cooperative co-evolution, scheduling problem, operational production planning

Introduction

Current trends in technology development open up great opportunities for the active transition of many companies to the use of Industry 4.0 technologies (Oztemel & Gursev, 2020). Industry 4.0 includes many different areas, such as automation, the implementation of cyber-physical systems, the creation of digital twins, increasing production flexibility, increasing productivity, and much more. One of the most important areas of Industry 4.0 (Saucedo-Martínez et al., 2018) is the development of intelligent decision support systems (DSS) for production systems (Alcácer & Cruz-Machado, 2019), including operational production planning (OPP) (Li et al., 2021).

There is one constant thing for any planning type for any scope of an organization as well as for any degree of automation - it is the need to choose an effective, and if possible, optimal solution, that means, solving optimization problems. This is useful in various situations such as decision support when choosing a set of projects to implement in production, concluding contracts to produce certain products, drawing up a schedule for the implementation of projects, or compiling shift-daily tasks, as well as rescheduling when the situation changes or when exiting equipment out of order.

A large gap between the theory of scheduling and its application in practice has been noticed for a long time (MacCarthy & Liu, 1993), however, due to the complexity of this problem, it has not been solved so far. Even though studies and special cases of the development of DSS for production planning are published, their dispersion according to the methods used and subject areas complicates the systematization of knowledge in this area. This is confirmed by a small number of meta-analyses and systematic reviews in the field of production scheduling, except in some of the most frequently published subject areas, such as energy-efficient planning (Gahm et al., 2016), work planning for open pit mining (Moghaddam & Moosavi, 2019), multidisciplinary production networks (Lohmer & Lasch, 2021). This is also because there are many types of scheduling problems, and it is impossible to create a universal scheduling system that can be applied to any task after a little revision and customization (Pinedo, 2012).

In this article, we focus on the consideration of universal formulations of the scheduling problem, which can be used in the broadest sense for any existing production model and propose a universal optimization approach for solving such problems.

Problem Statement

The Resource-Constrained Project Scheduling Problem (RCPSP) (Anichkin & Semenov, 2014) is a classic formulation for scheduling problems. The project consists of several works (activities) with a given processing priority. It is required to assign a start time for each activity, taking into account priority relationships and resource constraints, so that the duration of the entire project is minimal.

Considering this task within the framework of the OPP, we can say that the project is a certain batch (lot) on which it is necessary to perform a series of operations in the order specified by the technological process. It turns out that in case of production planning, we are talking about several RCPSPs that exist in parallel for each lot, which need to be solved simultaneously. Such a problem is difficult because even one RCPSP belongs to the class of NP-hard problems (Blazewicz et al., 1983).

RCPSP in practice for a real production process is so complex that it is extremely difficult to even find a feasible solution in the general formulation of the problem, even for one lot. On the other hand, operational production planning requires a quick solution, and any slightest violation of restrictions is unacceptable, since a critical condition for working with a real production process is to ensure its stability. Thus, it is extremely important to quickly find a feasible solution, so the use of a simulation model that guarantees the construction of only feasible solutions is reasonable and allows one to optimize some external model parameters, such as lot order or activity priorities.

Let us consider options for problem formulations that allow us to significantly reduce the dimension of the problem and avoid searching for feasible solutions, initially generating them exclusively in a feasible set. Let's define that there are several entities in the model, such as equipment (machine tools), employees, operations (activities) and technological processes. Each lot corresponds to one of the existing technological processes, which can be represented as a tree of operations (Figure 1). Also, the solution can be represented as a vector of n-dimensional space, since some non-linear sequence of operations can be converted to a string using some mapping.

See Full Size >

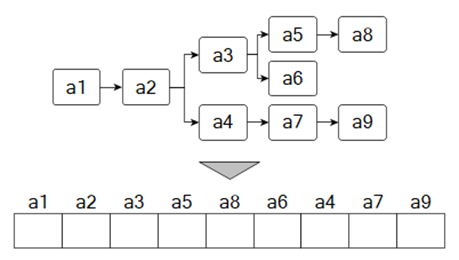
The RCPSP can be considered not only as a conditional optimization problem with real variables to find the start time of each operation, but also, for example, as a hierarchical problem, where at the top level there is a combinatorial optimization problem to determine the lot order, and the nested RCPSP is replaced by a simulation model with a greedy strategy. It can be called a hierarchical scheduling problem (Semenkina et al., 2019). In such formulation the problem of lot order determining is reduced to the traveling salesman problem. Figure 2 shows an example of coding a solution as lot order (LO). In this case, all operations of one lot have a higher priority than all operations of the other lot, and they will be scheduled earlier, but considering technological restrictions.

See Full Size >

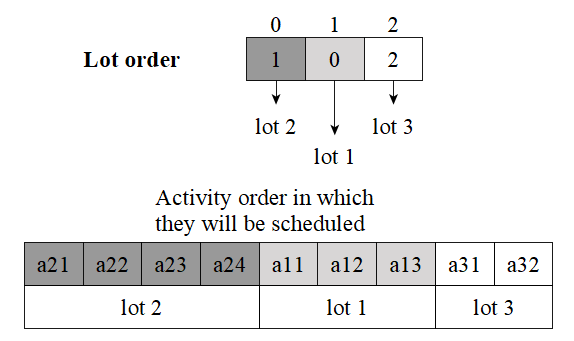
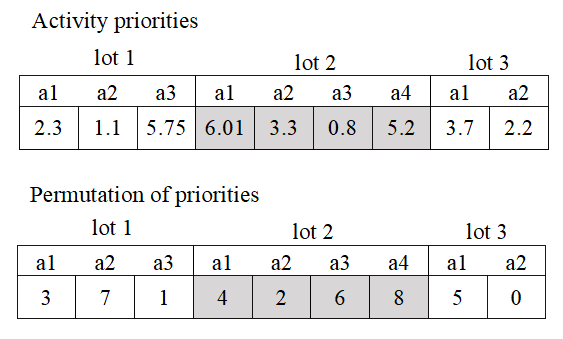
Two other options for presenting decisions are illustrated in Figure 3 activity priority (AP) or priority order (PO). At the beginning of the scheduling process, a list of available operations is determined, which consists of the first operations of all lots. At each step, from the operations in this list, the one with the highest priority is selected and scheduled. After removing this operation from the list, one must add to it all the following operations that have become available after the current one has been completed. The process continues until the list of operations become empty.

See Full Size >

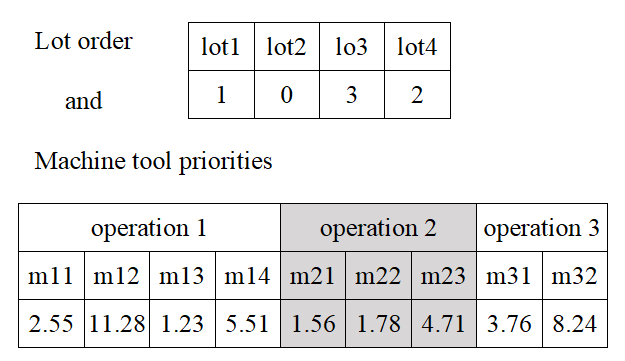
And the last of the problem statements under consideration is the hierarchical problem of lot order with a nested problem of machine tool priorities (LO-MTP). In this case, at the top level is the lot order problem discussed above. Additionally, after determining the order of the lots, the problem of equipment priority is solved to make the production more flexible. Thus, the operations for the lots will not be assigned to the first available machine tool, but to that which has a higher priority. This makes the model less greedy.

See Full Size >

Research Questions

In this study, the question of which general formulation of the scheduling problem shows the best efficiency was considered. Problem statements with a choice of lot order allow the use a production model of any complexity but have less flexibility. The question of research is to find out if they are as effective as problem formulations with operation priorities, which impose restrictions on the model in the form of the need to know in advance the sequence and number of operations for each lot before launch, which means that dynamically appearing operations, mixing batches and some other things are prohibited.

The second research question is to find out whether the use of the hierarchical self-configuring co-evolution is justified. This method helps to automate the choice of an algorithm for solving a problem and setting its parameters right at the time of solving the problem. This helps to simplify the use of intelligent technologies in practice by non-specialists.

Purpose of the Study

The purpose of the study is to improve the validity of decision-making when using intelligent technologies in the field of operational production planning by automating their design using hierarchical self-configuring co-evolutional algorithms.

Research Methods

According to a 2019 review (Liu et al., 2019), the most popular methods for solving scheduling problems are the genetic algorithm, the particle swarm algorithm, the bee colony algorithm, and the ant colony optimization. In this work, different algorithms are used for real and combinatorial optimization, but all of them have proven themselves well in their field. For real optimization, these are the genetic algorithm (GA) (Holland, 1975), the particle swarm optimization (PSO) (Bansal, 2019), and the differential evolution algorithm (DE) (Lampinen & Storn, 2004). For combinatorial optimization, it is also GA, Ant Colony Optimization (ACO) (Dorigo & Stützle, 2010), Intelligent Water Drops (IWDs) (Hosseini, 2007), and Lin-Kernighan Heuristics (LKH) (Lin & Kernighan, 1973).

All the algorithms mentioned above have many settings which must be selected for the problem being solved, that complicates their use, especially in practice. The solution to this problem is the use of the self-configuration method (Semenkin & Semenkina, 2012), which allows one to automate this process and not spend additional resources on choosing the algorithm settings. This approach, in addition to saving resources, allows the algorithm to be more flexible and better adapt to the problem at different stages of the optimization process. Thus, the following algorithms are considered here: Self-Configuring GA (ScGA), Self-Configuring PSO (ScPSO), and Self-Configuring DE (ScDE) for real optimization, as well as ScGA and ScACO for combinatorial optimization.

The next step in adapting the method to the problem in the process of solving is the automated selection of a self-configuring algorithm that is more suitable at the current moment. In this work, we use cooperative coevolution (CC) (Emelyanova & Semenkin, 2004). The main idea of CC is that the self-configuring algorithms work independently for a certain period, during which their performances are evaluated. After this period and evaluation of the algorithms, the computing resources are redistributed in such a way that the best algorithm gets more computing resources at the expense of the less efficient ones in this period. In addition, the best-known solutions are transferred to all algorithms, implementing the so-called migration, i.e., the algorithms are not only competing for computational resources but also cooperating by sharing all-round achievements.

Thus, to solve problems, a cooperative coevolutionary real optimization algorithm is used, which includes ScGA, ScPSO, and ScDE (ScCCreal), as well as a cooperative coevolutionary combinatorial optimization algorithm consisting of ScGA, ScACO, and IWDs (ScCCcomb). For hierarchical lot order problem with machine tool priorities nested problem were used ScCCcomb for top-level problem and ScCCreal for the nested one, so this is the hierarchical co-evolution method.

Findings

The study of the efficiency of solving problems in the formulations described above using cooperative coevolution of the described algorithms was carried out on six tasks generated using pseudorandom numbers with dimensions from 75 to 365 operations of all lots (Liu et al., 2019) (for the LO formulation of the same problems, it was from 10 to 60, respectively). All calculations were performed with the same number of objective function calculations. To collect statistical data, each algorithm with each setting was run 50 times independently. In addition, it is important to note that the criterion for evaluating solutions (the final duration of the plan, which should be minimized) due to the large dimension of the tasks, does not guarantee that the global optimum has been found, that means that only a comparison of the relative efficiency of algorithms and problem formulations is available.

To compare the efficiency of classical algorithms and their modified versions, the statistics of classical algorithms are used, averaged not only over runs but also over all algorithm settings. For example, for GA these are all possible combinations of all types of selection, crossing-over, mutation, for PSO - social and cognitive coefficients, as well as inertial weight. In addition to the average efficiency variant of the algorithm, the best algorithm is also given, that is, for example, GA (best) is a GA variant with settings that showed the best efficiency on the current problem.

Solutions to different problems differ greatly in absolute value, so the worst result was chosen for each of the problems, and then all the results of all algorithms were divided by this worst result. Thus, the solutions are presented on a scale from 0 to 1, where 1 is obviously the worst option, and the closer the value is to 0, the better solution was found.

Figures 5,6,7, and 8 show the results of all the algorithms described above for various problem formulations. Regardless of the formulation, there is an obvious tendency that the self-configuring version of the algorithm, of course, loses to the algorithm with the best settings on the problem, but outperforms the algorithm averaged over the settings. When someone solving real-world practical problems there is no way to spend computing resources on choosing the best settings, so the use of the self-configuration method is preferable in this case. This is also justified by the fact that the results obtained during the experiments show that on different tasks different settings have shown themselves to be the most effective.

In addition, co-evolution using self-configuring algorithms shows results comparable to the algorithms that compose it separately. ScCC has maximum flexibility in solving the problem and can adapt to each stage both by choosing an algorithm and by choosing its settings.

See Full Size >

See Full Size >

See Full Size >

See Full Size >

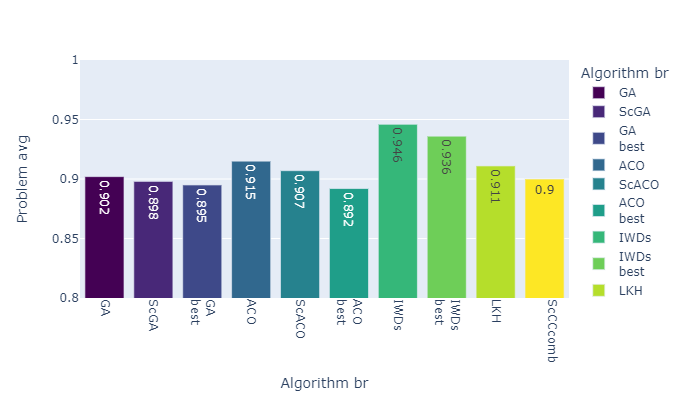
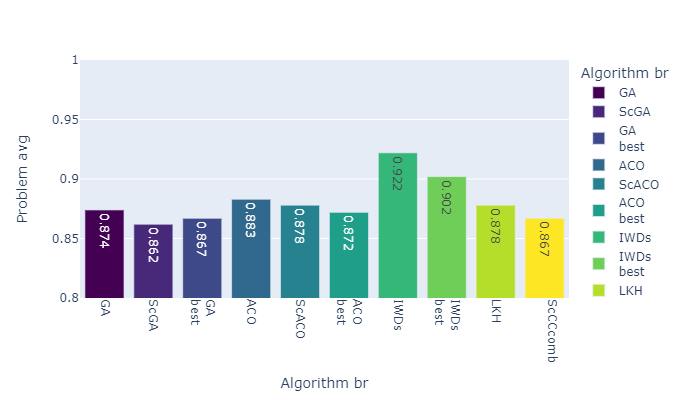
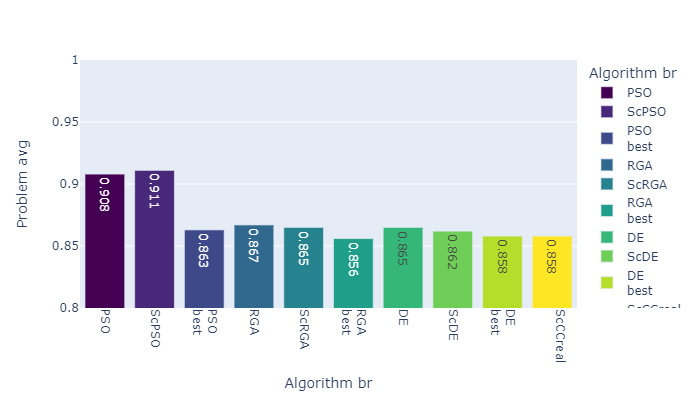
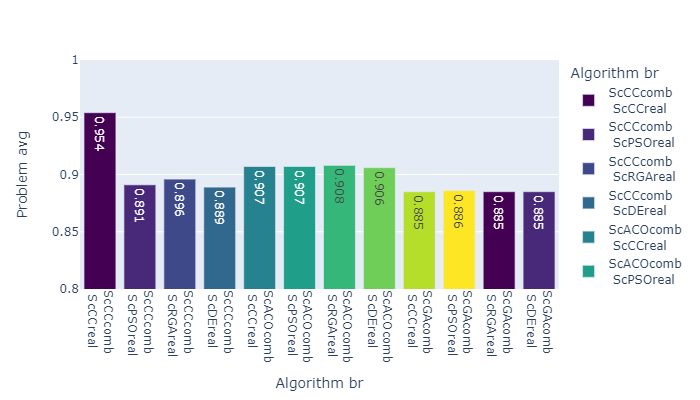
Separately, a comparison was made between different problem statements, namely, the choice of lot order, the order of priorities of operations, real priorities of operations, and lot order with nested machine tool priorities problem. Figure 9 shows the result for each problem, averaged over all the algorithms that were used for this problem. In Figure 10, the results are illustrated exclusively for co-evolution algorithms - ScCCcomb was used for lot order selection (LO) and priority order selection (PO), ScCCreal was used for real operation priority (AP) selection, and combination of ScCCcomb and ScCCreal (hierarchical co-evolution) for lot order with nested machine tool priorities problem (LO-MTP).

See Full Size >

See Full Size >

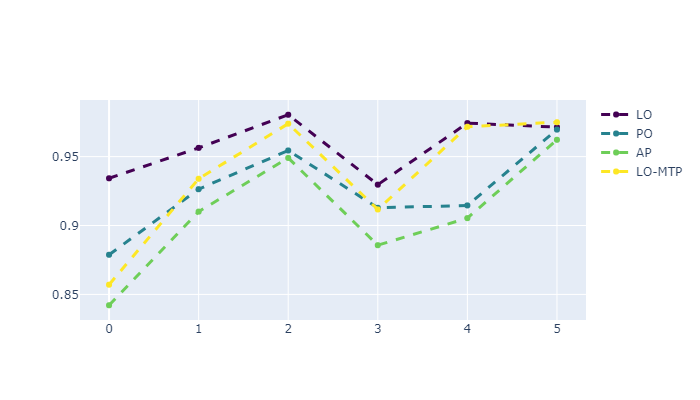
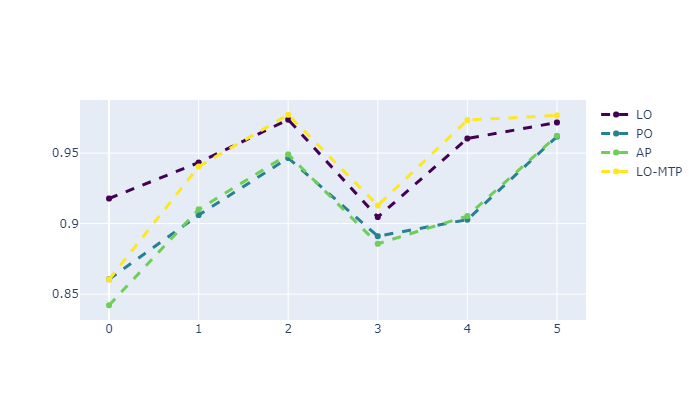
The LO problem has a significantly lower dimension, since it includes the order of only lots, fixing their strict prioritization between each other, while PO and AP have a dimension in the form of the sum of the number of all operations in all lots, which is ten times more. LO-MTP also has bigger dimension because it includes all amount of machine tools. It is interesting to note that this obviously makes the LO statement much less flexible, preventing more diverse solutions from being considered. However, the LO setting does not show the worst result for all problems but rather competes with the others on problems of higher dimensions. In addition, if we consider not only the result averaged over the algorithms, but also ScCC, then the LO formulation sows better results.

It is important to note that although the PO and AP formulations show the best efficiency on average, they are not applicable in practice in all situations, just like the classical RCPSP formulation, where the decision vector is the start point of all operations of all lots. This is due to the fact that in real production, often the technological process for the production of one lot cannot be predetermined step by step. For example, there are often accumulations of material up to a certain mass, which means that it is not possible to predict in advance which lots will be combined before building the schedule, since this is determined by the order of their arrival, and therefore the order of launch into production. In addition, many production processes can be described in the simulation model in the form of dynamically occurring events, the number and time of which cannot be predicted in advance.

Conclusion

The article considers and investigates bionic algorithms for real and combinatorial optimization, such as the genetic algorithm, the swarm particle optimization, the differential evolution, the ant colony optimization, and the intelligent water drops algorithm. Also, self-configuring versions of these algorithms were presented, and the cooperative co-evolutionary algorithm was proposed that effectively uses self-configuring bionic algorithms while solving the problem.

The self-configuration method shows competitive results that are superior to the classic algorithm averaged over its settings. Cooperative co-evolution of self-configuring bionic algorithms shows some of the best results on the problem and, in addition, often performs better than its individual components. In addition, such an integration of the two approaches significantly expands the possibilities of applying optimization algorithms in practice, since it does not require the involvement of experts in the field of bionic optimization algorithms.

The problem formulation of operational production planning through determining the lot order, despite slightly worse average results, performs well on problems of large dimensions and can be compared with two more flexible formulations - real priorities of operations and permutation of priorities of operations. In addition, this formulation has great potential for use in complex industries with technological processes that require non-standard methods of description. For more flexibility one can use also hierarchical lot order with nested machine tool priorities problem statement that shows competitive result.

Acknowledgments

This work was supported by the Ministry of Science and Higher Education of the Russian Federation (Grant № 075-15-2022-1121).

References

• Alcácer, V., & Cruz-Machado, V. (2019). Scanning the Industry 4.0: A Literature Review on Technologies for Manufacturing Systems. Engineering Science and Technology, 22, 899-919.

• Anichkin, A. S., & Semenov, V. A. (2014). A survey of emerging models and methods of scheduling. Proceedings of the Institute for System Programming of RAS, 26(3), 5-50. DOI:

  Google Scholar

  Crossref

• Bansal, J. C. (2019). Particle Swarm Optimization. In J. Bansal, P. Singh, & N. Pal (Eds.), Evolutionary and Swarm Intelligence Algorithms, Studies in Computational Intelligence (vol 779, pp. 11-23). Springer, Cham. DOI:

  Google Scholar

  Crossref

• Blazewicz, J., Lenstra, J. K., & Kan, A. H. G. R. (1983). Scheduling subject to resource constraints: classification and complexity. Discrete Applied Mathematics, 5(1), 11-24. DOI:

  Google Scholar

  Crossref

• Dorigo, M., & Stützle, T. (2010). Ant Colony Optimization: Overview and Recent Advances. In M. Gendreau, & J.-Y. Potvin (Eds.), International Series in Operations Research & Management Science (pp. 227-263). DOI:

  Google Scholar

  Crossref

• Emelyanova, M. N., & Semenkin, E. S. (2004). Study of the efficiency of the coevolutionary algorithm. Vestnik of the Siberian State Aerospace University named after Academician M.F. Reshetnev, 6, 28-34.

• Gahm, C., Denz, F., Dirr, M., & Tuma, A. (2016). Energy-efficient scheduling in manufacturing companies: A review and research framework. European Journal of Operational Research, 248(3), 744-757. DOI:

  Google Scholar

  Crossref

• Holland, J. H. (1975). Adaptation in Natural and Artificial Systems. The University of Michigan Press. DOI:

  Google Scholar

  Crossref

• Hosseini, H. S. (2007). Problem solving by intelligent water drops. Proceedings of IEEE Congress on Evolutionary Computation (pp. 3226-3231). IEEE. DOI:

  Google Scholar

  Crossref

• Lampinen, J., & Storn, R. (2004). Differential Evolution. In New Optimization Techniques in Engineering (pp. 123-166). Springer. DOI:

  Google Scholar

  Crossref

• Li, Y., Goga, K., Tadei, R., & Terzo, O. (2021). Production Scheduling in Industry 4.0. In L. Barolli, A. Poniszewska-Maranda, & T. Enokido (Eds.), Complex, Intelligent and Software Intensive Systems (pp. 355-364). DOI:

  Google Scholar

  Crossref

• Lin, S., & Kernighan, B. W. (1973). An Effective Heuristic Algorithm for the Traveling-Salesman Problem. Operations Research, 21(2), 498-516. DOI:

  Google Scholar

  Crossref

• Liu, Y., Wang, L., Wang, X. V., Xu, X., & Zhang, L. (2019). Scheduling in cloud manufacturing: state-of-the-art and research challenges. International Journal of Production Research, 57(15-16), 4854-4879. DOI:

  Google Scholar

  Crossref

• Lohmer, J., & Lasch, R. (2021). Production planning and scheduling in multi-factory production networks: a systematic literature review. International Journal of Production Research, 59(7), 2028-2054. DOI:

  Google Scholar

  Crossref

• MacCarthy, B., & Liu, J. (1993). Addressing the gap in scheduling research: a review of optimization and heuristic methods in production scheduling. International Journal of Production Research, 31(1), 59-79. DOI:

  Google Scholar

  Crossref

• Moghaddam, M., & Moosavi, E. (2019). A view on recent developments for production scheduling optimization. In Proceedings of the 26th International Mining Congress and Exhibition of Turkey (IMCET 2019), 166-173.

• Oztemel, E., & Gursev, S. (2020). Literature review of Industry 4.0 and related technologies. Journal of Intelligent Manufacturing, 31(1), 127-182. DOI:

  Google Scholar

  Crossref

• Pinedo, M. (2012). Scheduling. Springer.

• Saucedo-Martínez, J. A., Pérez-Lara, M., Marmolejo-Saucedo, J. A., Salais-Fierro, T. E., & Vasant, P. (2018). Industry 4.0 framework for management and operations: a review. Journal of Ambient Intelligence and Humanized Computing, 9(3), 789-801. DOI:

  Google Scholar

  Crossref

• Semenkin, E., & Semenkina, M. (2012). Self-configuring Genetic Algorithm with Modified Uniform Crossover Operator. Lecture Notes in Computer Science (pp. 414-421). Springer. DOI:

  Google Scholar

  Crossref

• Semenkina, O. E., Popov, E. A., & Ryzhikov, I. S. (2019). Hierarchical scheduling problem in the field of manufacturing operational planning. IOP Conference Series: Materials Science and Engineering, 537(3), 032001. DOI:

  Google Scholar

  Crossref