Minimizing the Carbon Footprint With the Use of Zeroing Neural Networks

Abstract

This article describes development and application of the approach of using the zeroing neural network (ZNN) to solve the problems of optimizing the carbon footprint emission on the example of the system approach model. The model described is an integrated optimization problem based on the previously developed by other authors of the model and the method of zeroing neural networks. Optimization problem, which is defined by the objective function that represents the minimization of carbon emissions and limitations, is complex. To solve this problem, an approach based on the use of zeroing neural networks was established. The model is an upgraded version of the original model. In this paper, we investigate the possibility of creating a system to minimize the carbon footprint. The system is built on the principles of production planning, which means there is no need for major changes, such as equipment changes. The system takes into account all the necessary indicators for the successful economic existence of the enterprise. When developing such a system, the balance between financial costs and carbon emissions is very important. Accordingly, the optimization task in this case is complex: minimization of the carbon footprint must correspond to the minimization of the costs of the enterprise.

Keywords: Carbon footprint, zeroing neural networks, optimization

Introduction

Greenhouse gas emissions cause climate change, and their impact on the environment continues to increase. As a result, there is an urgent need to accelerate efforts to minimize the carbon footprint. In industry, most modern methods of reducing greenhouse gas emissions depend on technical improvements to the facility and equipment. These methods are focused on local optimization to reduce carbon emissions in enterprises and may require additional time, money and effort to implement satisfactorily (Guo & Zhang, 2012; Su et al., 2017; Uhlig, 2020).

Currently, most work on carbon footprint analysis focuses on the macro and micro levels. However, we can only influence these levels by dealing with the problem on a point-by-point basis. One opportunity to make a difference is to help businesses track and minimizing their carbon footprint with minimal financial loss. The purpose of carbon footprint analysis in enterprises is to identify the production processes that have the greatest impact on emissions and their subsequent planning. In this case, planning based on the analysis can become an excellent assistant for managers of the enterprise (Chen & Yi, 2016; Li et al., 2013).

In contrast to technical approaches that focus on equipment, this paper proposes an approach that combines carbon footprint analysis and optimization of dynamic systems through a nullifying neural network.

In this article, we adapt the nullifying neural network method to the model of a systems approach combining carbon footprint analysis and production planning developed by authors Qiang Sua, Wei Yang and Yaowu Liu in their paper "Optimizing Carbon Emissions with Enterprise-Level Production Planning".

Problem Statement

Su et al. (2017) in his work "Optimization of carbon emission considering production planning at enterprise level" published by Journal of Cleaner Production wrote:

Direct greenhouse gas emissions are mainly caused by the combustion of fuels in stationary sources, industries and the processing of chemicals and materials. Indirect emissions are the result of generating purchased electricity that is consumed by equipment or operations. Based on the accounting and calculation methodologies provided by the Intergovernmental Panel on Climate Change (IPCC), both direct and indirect greenhouse gas emissions are calculated in terms of CO2 equivalence over a 100-year time horizon. (p. 637)

The purpose of this work is to apply the method of zeroing neural networks to the model of the system approach to minimizing the carbon footprint presented in Figure 1.

See Full Size >

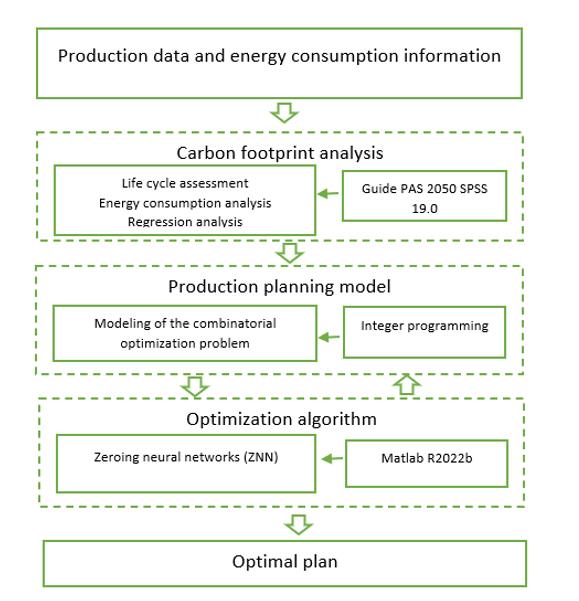
According to “the algorithm, an integer programming model was developed. Integer programming and mixed integer programming models are always used to solve the problem of production planning” (Su et al., 2017, p. 635). The model is formulated as follows:

$min{\sum }_{d\in H}^{}CE\left(x_d\right)$ (1)

${\sum }_{l\in L_{p_i}}^{}{\sum }_{d\in H}^{}{x}_{p_i,ld}\ge R_{p_i},\forall p_i\in P$ (2)

$x_{p_i},ld\le y_{p_i,ld}{C}_{p_{i}l},\mathrm{}\forall p_i\in P,l\in L,d\in H$ (3)

${\sum }_{p_i\in P}^{}{y}_{p_i,ld}\le 1,\forall l\in L,d\in H$ (4)

${\sum }_{l\in L{C}_n}^{}{y}_{p_i,ld}\le \mathrm{1},\mathrm{}\forall L{C}_n\in LC,p_i\in P,d\in H$ (5)

Where 1 – Minimizing carbon emissions for production plans $x_d$, 2 - restriction on the fulfillment of demand for products, 3 - Capacity constraints, 4 – restrictions that fix the possibility of producing only one type of product per day on one production line, 5 – restrictions on the simultaneous operation of some production lines due to limited resources.

In turn, in our work, we develop an algorithm for a zeroing neural network to determine the optimal solution that can be useful in real situations.

Research Questions

The development and application of the approach of using the zeroing neural network (ZNN) to solve the problems of optimizing the carbon footprint emission on the example of the system approach model.

Purpose of the Study

A scheme for carbon footprint planning and accounting for economic parameters such as demand satisfaction and economies of scale. Accordingly, it is a multi-purpose task of optimizing the processes managed by the managers of the enterprise. Execution of which will lead to minimization of total emissions versus minimization of total costs.

Research Methods

The ZNN method was proposed twenty years ago by Yun Zhang and Jun Wang in 2001:

ZNN methods have become the basis for solving discretized matrix problems controlled by sensors in real time, in theory and in embedded applications for robots, in control theory and engineering in general. They have become the method of choice for many time-varying matrix tasks that benefit from or require efficient, accurate, and predictive real-time computing. A typical ZNN algorithm requires seven separate steps to configure. (Bunse-Gerstner et al., 1991, pp. 20-21)

Step 1. From model equation (1), form an error function E(t) = F(A(t), B(t), x(t), ..) − g(t, C(t), u(t), ..) (2), which would be identical to zero, i.e. E(t) = 0 for all t if x (t) solves (1).

Step 2. Take the derivative of the E(t) error function E(t) and determine its exponential decline. Require that E(t) = −η E(t) (3) for some constant η > 0.

Step 3. Solve the exponentially decreasing error equation differential equation (3) of step 2 algebraically for x (tk) = . . . if possible. If this is not possible, review the starting model and try again.

Step 4. Select a predicted convergent formula of finite differences for the desired truncation error order O(τ j) that ZNN and time-varying matrix streams 3 express x(tk) in terms of x(tk +1), x(tk), ..., x(tk + 1-j ), i.e. in terms of j + 1 known data points.

Step 5. Equate the derived terms x(tk) in steps 3 and 4 and thus get rid of x(tk) completely.

Step 6. Solve the linear equation without derivative obtained in step 5 for x (tk +1) and iterate.

Step 7. Increase k + 1 to k + 2 and increase all step 6 data; then decide the updated recursion for x (tk + 2). And repeat until t... ≥ tf .

ZNN uses 1st order time derivatives and they are successfully used to optimize time-varying matrix minimization tasks, all in real time. From a given time-varying matrix or vector problem, all ZNN methods form a problem-specific error function e(t), which must decrease exponentially to zero, both globally and asymptotically, according to the formula e(t) = −ηe (t) for the decay of a constant η > 0.

To solve optimization problems based on ZNN, a software platform has been developed in the Matlab application package and is published by reference to https://www.researchgate.net/publication/ 255602767_Methods_for_Constrained_Optimization.

Findings

Thus, using a software platform to solve the optimization problem by the method of zeroing neural network, we obtained ZNN solutions for optimizing CO2 emissions. The following results with input parameters of the two-week period were obtained:

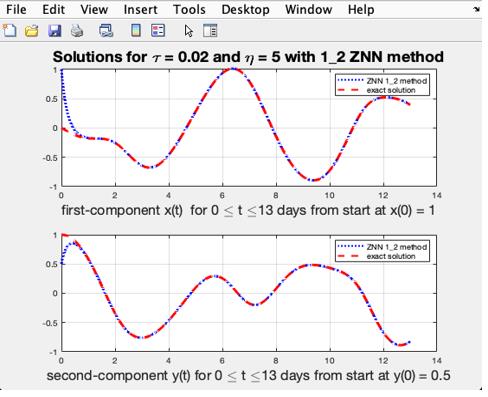
Solutions for T = 0.02 and H = 5 by method 1\_2 ZNN are shown in Figure 2.

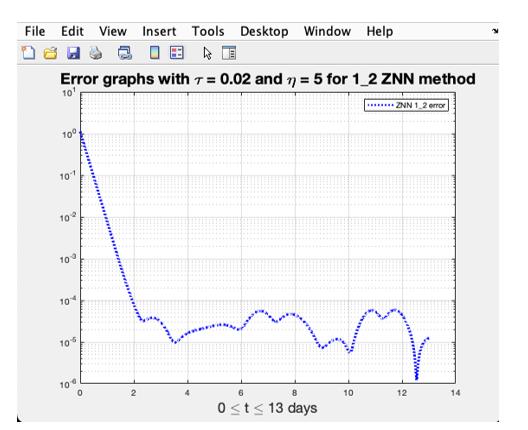
The error graphs with T = 0.02 and H = 5 for ZNN method 1\_2 are shown in Figure 3.

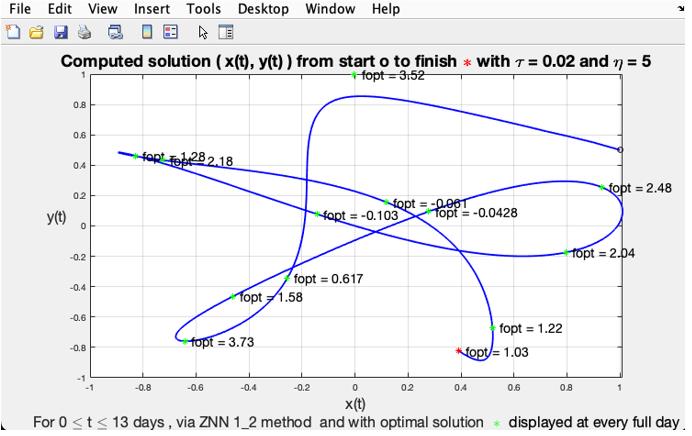
The calculated solution (x(t), y(t) from start o to end\color{red} \cast\color{black} with \tau = 0.02 and \eta = 5 is shown in Figure 4.

See Full Size >

See Full Size >

See Full Size >

Conclusions

This paper uses carbon gas emission optimization on the basis of heuristic optimization to minimize logistics costs and carbon emissions based on zeroing neural networks.

The model described in the paper is an integrated optimization problem based on the model previously developed by other authors and the method of zeroing neural networks. The optimization task, which is described by the objective function of minimizing carbon emissions and limiting, is complex. To solve this problem, an approach based on the use of zeroing neural networks was established. The developed model is an improved version of the original model. Its effectiveness has been investigated and confirmed by benchmarking.

This method incorporates carbon footprint minimization analysis using zeroing neural networks to solve the production scheduling problem. By analyzing production processes, we have developed a model that demonstrates the relationship between production processes and the scheduling of these activities. This model will help to build an optimal plan with respect to production processes and carbon emissions.

Because of the complexity of the planning model, if a manager uses the proposed software, he can get a good solution in a short time to solve a practical problem.

A computational experiment showed that optimizing the work plan can improve energy efficiency and reduce carbon dioxide emissions at the plant. By producing the same number of products and not delaying delivery times, the proposed method can reduce carbon dioxide emissions. The model can also be applied to other problems of a similar nature, in particular minimization. And even solving the problem of minimizing the carbon footprint in complex computations on distributed heterogeneous information processing systems.

Acknowledgments

This work was supported by the Ministry of Science and Higher Education of the Russian Federation (grant No. 075-15-2022-1121).

References

• Bunse-Gerstner, A., Byers, R., Mehrmann, V., & Nichols, N. K. (1991). Numerical computation of an analytic singular value decomposition of a matrix valued function. Numerische Mathematik, 60(1), 1-39. DOI:

  Google Scholar

  Crossref

• Chen, K., & Yi, C. (2016). Robustness analysis of a hybrid of recursive neural dynamics for online matrix inversion. Applied Mathematics and Computation, 273, 969-975. DOI:

  Google Scholar

  Crossref

• Guo, D., & Zhang, Y. (2012). Zhang neural network, Getz-Marsden dynamic system, and discrete-time algorithms for time-varying matrix inversion with application to robots' kinematic control. Neurocomputing, 97, 22-32. DOI:

  Google Scholar

  Crossref

• Li, S., Chen, S., & Liu, B. (2013). Accelerating a Recurrent Neural Network to Finite-Time Convergence for Solving Time-Varying Sylvester Equation by Using a Sign-Bi-power Activation Function. Neural Processing Letters, 37(2), 189-205. DOI:

  Google Scholar

  Crossref

• Su, Q., Yang, W., & Liu, Y. (2017). Optimization of carbon emission considering production planning at enterprise level. Journal of Cleaner Production, 162, 635-645. DOI:

  Google Scholar

  Crossref

• Uhlig, F. (2020). Coalescing Eigenvalues and Crossing Eigencurves of 1-Parameter Matrix Flows. SIAM Journal on Matrix Analysis and Applications, 41(4), 1528-1545. DOI:

  Google Scholar

  Crossref