Identification of Differential Equations Systems With Various Input Effects

Abstract

Nowadays, differential equations and their systems are one of the most preferred ways to represent models of dynamic objects. Objects from different areas are dynamic. Therefore, a great number of methods for dynamical systems identification have been developed. However, as processes become more complex, there exist a need to develop new tools. A change in the input action according to a predetermined law could be one of features for dynamic processes. The paper studies the efficiency of the method based on evolutionary algorithms to identify objects in the form of systems of differential equations with various input effects. Genetic programming and differential evolution are the algorithmic basis of the method. The method performs self-configuring of parameters for evolutionary algorithms. The presented paper studies efficiency of the proposed method on five problems where the initial objects are represented by systems of differential equations of various orders. The conducted study takes into account the presence of noise in the initial samples. It demonstrates graphical interpretation of the obtained results. The obtained results prove efficiency of the developed method under various input influences.

Keywords: Differential equation, identification, evolutionary algorithms

Introduction

Mathematical modeling of dynamic systems is an interdisciplinary tool for studying various processes in nature, society and industry. A lot of methods have been developed to simulate dynamic processes. These methods belong to the analytical and numerical, parametric and nonparametric classes (Brester et al., 2020; Ovcharenko, 2020; Roehrl et al., 2020). The study of various systems’ behavior often leads to analysis and solution of equations that include characteristics such as a rate of change of system parameters. An analytical representation of such changes are derivatives. They are the basis of differential equations. Differential equations and their systems are the basis for studying in the mathematical modeling field. They are functionally applied in manufacturing. It is extremely important for the development of various branches of science and technology (Brester & Ryzhikov, 2019; Liu et al., 2021).

The theory of differential equations is characterized by its direct application for practical problems (Chu & Marynets, 2021). Differential equations and their systems can be applied as a tool for modeling various phenomena in mechanics, chemical reactions, electrical and magnetic phenomena (Escalante-Martínez et al., 2020). The study of a wide range of problems connected with the strength of materials, biology, economics shows that their solution is reduced to mathematical modeling in the form of a functional dependence described by differential equations and their systems. The representation in the form of differential equations makes it possible to obtain a model that is suitable for further study. In this aspect, it is necessary to take into account the interpretability of the obtained results provided by the symbolic representation of differential equations. It is worth noting that they often contain not one, but several output characteristics when studying manufacturing processes. Systems of differential equations are applied to represent such processes.

The paper analyzes a method based on a self-configuring genetic programming algorithm for identification of dynamic systems with input effects changing according to predetermined laws.

Problem Statement

Let it need to be solved the inverse problem of mathematical modelling for a process characterized by an arbitrary number of input and output variables, i.e., build a model in the form of a system of differential equations according to the measurements of inputs and outputs:

$\left\{\begin{array}{c}{y}_{\mathrm{1}}^{\left(k\right)}=f_{\mathrm{1}}(t,\mathrm{}{x}_{\mathrm{1}},\mathrm{}\dots ,x_m,y_{\mathrm{1}},\dots ,y_s)\\ y_{\mathrm{2}}^{\left(k\right)}=f_{\mathrm{2}}(t,\mathrm{}{x}_{\mathrm{1}},\mathrm{}\dots ,x_m,y_{\mathrm{1}},\dots ,y_s)\\ \dots \\ y_s^{\left(k\right)}=f_s(t,\mathrm{}{x}_{\mathrm{1}},\mathrm{}\dots ,x_m,y_{\mathrm{1}},\dots ,y_s)\end{array}\right.$

where are measurements of input variables, are measurements of output variables, and are their numbers, respectively, is an order of the differential equation.

It should be taken into account that input effects can be changed according to the certain laws.

Research Questions

The presented work explores the following research questions:

• What evolutionary methods make it possible to obtain a model of a dynamic object in the form of differential equations and their systems?
• Is it possible to apply the method based on evolutionary algorithms to identify dynamic objects with input effects changed according to certain laws?

Purpose of the Study

The purpose of this work is to develop and study a method based on evolutionary algorithms for the dynamic objects identification in the form of differential equations systems. The authors study the efficiency of the approach for various inputs.

Research Methods

The paper studies the method, proposed by the authors, for the identification of dynamic objects in the form of differential equations systems. The scheme of the method is presented in Figure 1:

See Full Size >

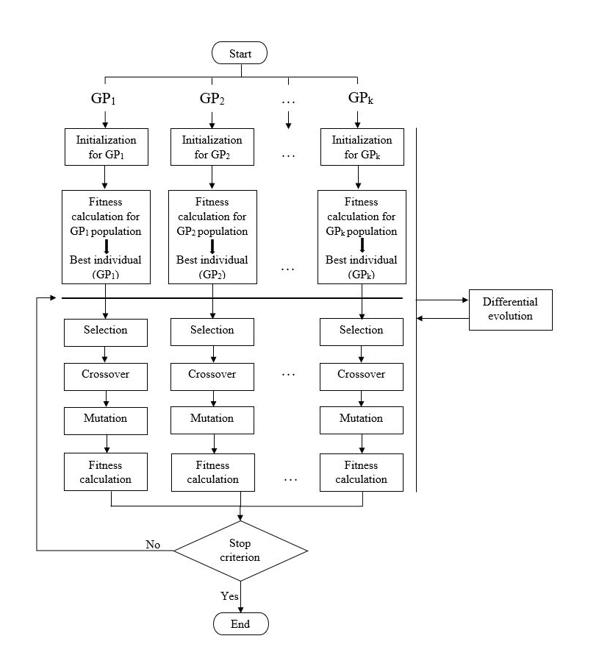
The considered method is characterized by the following features:

$fitness=\frac{\mathrm{1}}{\mathrm{1}-error},$

$error=\mathrm{}\frac{\underset{i=\mathrm{1}}{\overset{k}{\sum }}\underset{j=\mathrm{1}}{\overset{n}{\sum }}{\left(y_{ij}-{\hat{y}}_{ij}\right)}^{\mathrm{2}}}{sn},$

where is sample size, is number of equations, are values from the original sample, ${\hat{y}}_{ij}$ is value of the model.

The calculation of fitness (equation) for each individual in each population is carried out by substitution into each of the equations of the system. The best individuals are selected as remaining equations.

Thus, the method helps to encode a system of differential equations of an arbitrary number of equations of an arbitrary order.

Findings

Table 1 presents systems of differential equations that were applied to study the considered method.

The dependences presented in Figure 2 were selected as input effects.

See Full Size >

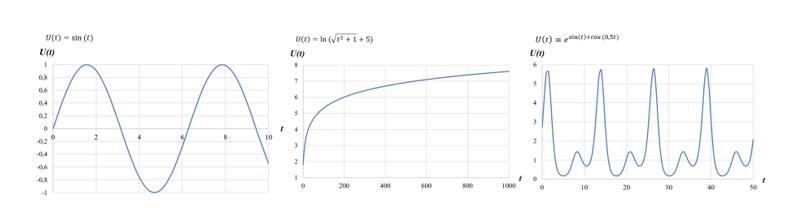
Data with different levels of noise (5%, 10%) were generated based on each system of differential equations and input effects. The sample size for each set was 30 points. Thus, 9 data sets were given for each system. Also, 30 runs were carried out for each set. Table 2 presents error values for the given conditions averaged over 30 runs.

Regression analysis are as follows (Table 2):

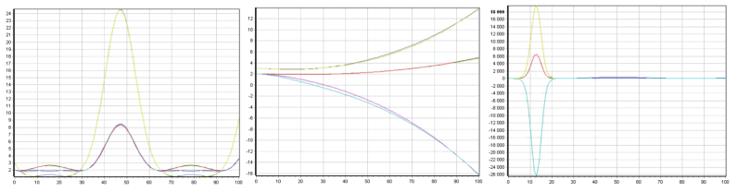
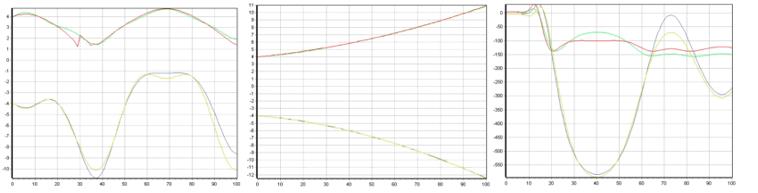
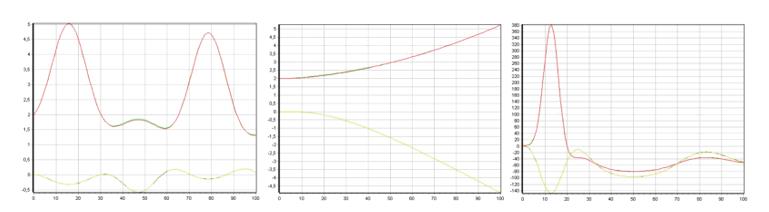
Figures 3-7 present the correspondence graphs of the obtained models to the original samples. Green and blue lines indicate outputs of the original objects, red and yellow lines correspond to the outputs of the obtained models (if there are more than two outputs, violet lines are outputs of the original objects and light blue lines are outputs of the obtained models). Complete line overlap with minimal model error is possible.

See Full Size >

See Full Size >

See Full Size >

See Full Size >

See Full Size >

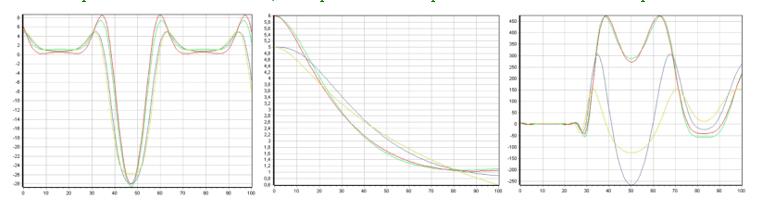
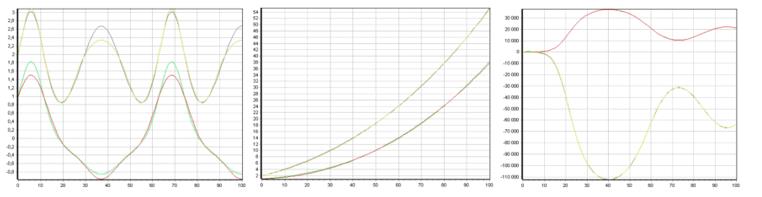
Conclusion

In the course of the work, the study of the quality of identification in the form of differential equations systems for different input influences was conducted. Objects are represented by differential equations systems of various types and orders. The resulting models describe the data well regardless of the type of input effects. It is confirmed graphical interpretation of the obtained values.

Acknowledgments

This work was supported by the Ministry of Science and Higher Education of the Russian Federation (Grant № 075-15-2022-1121).

References

• Brester, C., & Ryzhikov, I. (2019). Tuning Parameters of Differential Evolution: Self-adaptation, Parallel Islands, or Co-operation. In J. J. Merelo, J. Garibaldi, A. L. Barranco, K. Madani, & K. Warwick (Eds.), Proceedings of the 11th International Joint Conference on Computational Intelligence IJCCI (pp. 259-264). DOI:

  Google Scholar

  Crossref

• Brester, C., Ryzhikov, I., Stanovov, V., Semenkin, E., & Kolehmainen, M. (2020). Nonlinear dynamic system identification with a cooperative population-based algorithm featuring a restart metaheuristic. IOP Conference Series: Materials Science and Engineering, 734(1), 012100. DOI:

  Google Scholar

  Crossref

• Chu, J., & Marynets, K. (2021). Nonlinear Differential Equations Modeling the Antarctic Circumpolar Current. Journal of Mathematical Fluid Mechanics, 23(4), 92. DOI:

  Google Scholar

  Crossref

• Escalante-Martínez, J. E., Morales-Mendoza, L. J., Cruz-Orduña, M. I., Rodriguez-Achach, M., Behera, D., Laguna-Camacho, J. R., López-Calderón, H. D., & López-Cruz, V. M. (2020). Fractional differential equation modeling of viscoelastic fluid in mass-spring-magnetorheological damper mechanical system. The European Physical Journal Plus, 135(10), 847. DOI:

  Google Scholar

  Crossref

• Karaseva, T., & Semenkin, E. (2022). Evolutionary Approaches to the Identification of Dynamic Processes in the Form of Differential Equations and Their Systems. Algorithms, 15(10), 351. DOI:

  Google Scholar

  Crossref

• Liu, R., Bianco, M. J., & Gerstoft, P. (2021). Automated partial differential equation identification. The Journal of the Acoustical Society of America, 150(4), 2364-2374. DOI:

  Google Scholar

  Crossref

• Meyer-Nieberg, S., & Beyer, H.-G. (2007). Self-Adaptation in Evolutionary Algorithms. Parameter Setting in Evolutionary Algorithm, 54, 47-75. DOI:

  Google Scholar

  Crossref

• Ovcharenko, V. N. (2020). Structural-Parametric Identification of a Linear Dynamic System with Constant Parameters. Automation and Remote Control, 81(1), 1-12. DOI:

  Google Scholar

  Crossref

• Roehrl, M. A., Runkler, T. A., Brandtstetter, V., Tokic, M., & Obermayer, S. (2020). Modeling System Dynamics with Physics-Informed Neural Networks Based on Lagrangian Mechanics. IFAC-PapersOnLine, 53(2), 9195-9200. DOI:

  Google Scholar

  Crossref

• Storn, R., & Price, K. (1997). Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. Journal of global optimization, 11(4), 341-359. DOI:

  Google Scholar

  Crossref