Abstract
Credit card customers comprise a volatile subset of a banks' client base. As such, banks would like to predict in advance which of those clients are likely to attrite, so as to approach them with proactive marketing campaigns. Neuronets have found great application in many classification problems. Credit card attrition is a poorly investigated subtopic that poses many challenges, such as highly imbalanced datasets. The goal of this research is to construct a feed-forward neuronet that can overcome such obstacles and thus accurately classify credit card attrition. To this end, we employ a weights and structure determination (WASD) algorithm that facilitates the development of a competitive and all around robust classifier whilst accounting for the shortcomings of traditional back propagation neuronets. This is supported by the fact that when compared with some of the best performing classification models that MATLAB's classification learner app offers, the power softplus activated WASD neuronet demonstrated either superior or highly competitive performance across all metrics.
Keywords: Neuronets, weights and structure determination, classification, credit card attrition
Introduction
The growth of a company depends significantly on the efforts that the entity makes towards: maintaining and growing its existing customer base, acquiring/keeping up with new technology, focusing on specific market segments, and improving its productivity and efficiency. This is especially true in highly competitive and mature business sectors, such as the banking sector (Hu, 2005). It is asserted that the first of these criteria is also the most obvious. In particular, more and more businesses are realizing that their current client base is their most valuable asset (García et al., 2017). It is not surprising that service providers in the financial sector go to considerable lengths to entice customers away from their rivals while minimizing their own losses (He et al., 2014).
Nevertheless, clients themselves have also grown aware of the value of their customer base, not only the banks. Another factor enhancing the already competitive atmosphere is the latter party's growing knowledge of the quality of the services offered. That is, a customer will frequently abruptly stop doing business with a bank and go to a rival company because of considerations like accessibility or even a more enticing interest rate (Farquad et al., 2014). Because of the impact that even a slight increase in customer retention can have on the banks' income statement along with the well-established facts that maintaining is significantly less expensive than re-acquiring lost customers, financial institutions have been motivated to gradually change their focus from attracting new customers to retaining as many of their existing ones (Tang et al., 2014).
The importance of knowing ahead of time who of their clients, starting with the high return on investment clients, are likely to quit has increased for banks (He et al., 2014). When a financial institution has this information, it may run targeted marketing programs that have been proven to be quite successful at keeping customers (Hu, 2005). Due to the importance and high demand from financial institutions, this research introduces a neuronet (also known as neural network) for credit card attrition classification. It is worth mentioning that from a business standpoint, attrition is the gradual but intentional loss of customers or staff that happens as they leave a company and are not replaced.
Artificial neuronets have been successfully applied to a wide spectrum of fields, including but not limited to medicine, such as in the prediction of breast cancer (Ed-daoudy & Maalmi, 2020) and economics and finance, such as in the classification of firm fraud (Simos et al., 2022), in the analysis of time series (Zhang et al., 2019), in portfolio optimization (Mourtas & Katsikis, 2022) as well as in the prediction of various macroeconomic measures (Zeng et al., 2020). Furthermore, there is an abundance of applications in problems stemming from the various engineering disciplines. For example, artificial neuronet models have been applied to performance analysis of solar systems (Esen et al., 2009), remote sensing multi-sensor classification (Bigdeli et al., 2021), predict flow behavior of alloy (Huang et al., 2018), performance analysis of heat pump systems (Esen et al., 2017). This research introduces and investigates a novel feed-forward neuronet (FFN), which uses a weights and structure determination (WASD) training algorithm, for classifying credit card attrition.
The following are the main points of this research: a novel power softplus WASD (PS-WASD) neuronet for addressing classification problems is presented; the PS-WASD neuronet's performance is compared to some of the best performing MATLAB's classifiers, as well as a Bernoulli WASD (B-WASD) neuronet (Zhang et al., 2019), on a publicly accessible credit card attrition dataset.
Problem Statement
The most popular training algorithm for FFNs is the back-propagation error algorithm. However, traditional back-propagation neuronets come with a few shortcomings, namely: they are characterized by high computational complexity, especially on the grounds of obtaining an optimal structure; the selection of suitable hyper-parameters, a rather difficult task, can often make or break the neuronet's performance; there is high risk of converging to a sub-optimal solution. To address these shortcomings, the alternative training algorithm WASD is proposed (Zhang et al., 2019).
Newly implemented WASD training algorithms offer a feature that their predecessors lack. Namely, the weights direct determination (WDD) process, inherent in any WASD algorithm, facilitates the direct computation of the optimal set of weights, hence allowing one to avoid getting stuck in local minima and all in all contributing in the achievement of lower computational complexity (Simos et al., 2022; Zhang et al., 2019). In this paper, a PS-WASD neuronet will be applied to a publicly available credit card attrition dataset and its' performance will be compared to other popular classifiers that MATLAB's classification learner app offers, namely linear support vector machines (SVM), fine k-nearest neighbors (KNN), kernel naive bayes (KNB), as well as the B-WASD neuronet.
Research Questions
This research proposes a PS-WASD neuronet to deal with the problem of classifying credit card attrition. Does the PS-WASD training algorithm, however, allow for the construction of a neuronet that matches (or potentially surpasses) the performance of benchmark classifiers, such as models coming from MATLAB's classification learner app? The findings of this paper demonstrate that this is in fact feasible. We construct a 3-layer PS-WASD based FFN that, as far as the dataset in question is concerned, outperforms a number of well-established high performing. Additionally, we study the question if the PS-WASD algorithm perform even better than the already established WASD, such as those in (Zhang et al., 2019). The results of the experiments show that the PS-WASD is more accurate and precise.
Purpose of the Study
In this study, a FFN is used to classify credit card customers that are likely to attrite. The purpose is to develop a WASD classifier that can rise to the task. As a result, financial institutions that can acquire that knowledge for their client base obtain a competitive advantage in the form of operating cost reduction.
Research Methods
This section describes the 3-layer PS-WASD based FFN model which has input and hidden layer neurons. Particularly, Layer 1 is the input layer that receives and allocates the input values to the corresponding neuron in Layer 2, which has a maximum number of activated neurons of , with equal weight 1, whereas Layer 3 is the output layer and has one activated neuron. The weights in neurons link between Layer 2 and Layer 3 are obtained via the WDD process. By using the PS-WASD algorithm, the neuronet model can achieve minimal hidden layer utilization.
The PS-WASD Based Neuronet
Let = be the normalized input matrix in the interval with denoting the number of the samples and be a binary target vector. Notice that in order to avoid over-fitting, the inputs must be normalized in the interval , which can be done by applying the following transformation (Zhang et al., 2019): . It should also be noted that all operations on are element-wise in this section.
Assume that there exists an underlying relationship such that . The neuronet aims at approximating through a linear combination of activation functions , where is the power softplus activation as in (Simos et al., 2022), with . For each activation , let denote the image of under . Thus, . Assuming a weights vector , a linear combination of all images may be written as , where . Note that , the neuronet's output, must be converted to binary. To this end, an element-wise function is employed so that the final output of the neuronet is with
where 1 implies a customer that is likely to attrite and vice versa. On the convergence of the neuronet, the following Theorem 1 and Proposition 1 should be noted.
Let be a nonnegative integer and assume a target function that has the -order continuous derivative on interval , then for ,
(1)
where is a polynomial used to approximate and is the error term.
Given a constant value , can be approximated as:
(2)
where is the value of the -order derivative of at , implies the factorial of , and signifies the K-order Taylor polynomial of function .
Theorem 1 can be used to approximate multivariable functions (Zhang et al., 2019). For a target function with -order continuous partial derivatives in an origin's neighborhood and variables, the -order Taylor polynomial to the origin is:
(3)
where are nonnegative integers.
Based on the aforementioned analysis, the optimal weights can be obtained through the WDD process (Zhang et al., 2019) as follows:
(4)
where denotes the pseudo-inverse of .
The PS-WASD Algorithm
With the computation of the optimal weights being handled by (4), the next concern is the determination of the optimal size for the neuronet. This is done through the PS-WASD algorithm that is employed in conjunction with cross validation so as to ensure that the model generalizes beyond the set of training. The PS-WASD algorithm can be described in the following three steps.
Considering the normalized input matrix , the training and testing sets are determined by a random split. The training set is once again divided into two sets of samples, one for model fitting and the other for validation. The parameter , which is set by the user, represents the percentage of samples that is to be allocated for model fitting purposes.
Assuming that the training set consists of samples, we use the first samples for fitting the model, and the rest samples for validation. Starting from the power and an empty matrix , the PS-WASD algorithm grows by adding the respective columns , whilst incrementing . In each iteration, the optimal weights are computed with respect to the training set as in Eq. 4 and the current performance of the neuronet is assessed on the validation set through a metric of choice, namely the mean-absolute-error (MAE ). Added columns are only kept if their addition has resulted in a performance boost; that is, a lower MAE.
This process is repeated until reaches a predefined threshold, which we set to be . In reaching , the training and validation sets are brought together and the final set of weights is computed relative to all available training and validation samples.
To conclude, the PS-WASD training algorithm not only guarantees that the weights are optimal, but also facilitates future computation by growing the neuronet's structure to the smallest size possible. In combination with cross validation as described above, the PS-WASD training algorithm is indeed a powerful tool.
Findings
With the neuronet having obtained it's final structure, all that is left is to apply it on the testing set. It is worth mentioning that the credit card attrition dataset used for evaluating the neuronets performance is available at https://www.kaggle.com/datasets/jaikishankumaraswamy/customer-credit-card-churn, and includes 33 variables and 1 target. Figures 1a and 1b depict the training error path the classification results on the testing set of the PS-WASD under , respectively, whereas Tables 1 and 2 evaluate the PS-WASD performance against other popular classifiers. It bears mentioning that the abbreviation 'CCC' in the rightmost Figure stands for credit card customer.
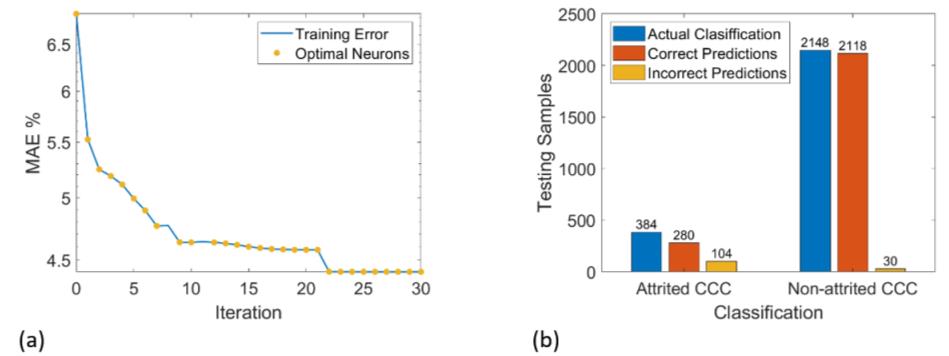
To be able to extract meaningful conclusions as to the competency of the proposed PS-WASD neuronet, a comparison with other well performing classifiers is in order. To that end, we picked three popular models from MATLABs' classification learner app, namely, KNB, Linear SVM and Fine KNN, as well as the B-WASD. All models are evaluated on the basis of nine metrics, namely, MAE, TP, FP, TN, FN, Precision, Recall, Accuracy and F-measure, where TP, FP, TN, FN stand for true positive, false positive, true negative and false negative rate, respectively. Except for MAE, the rest of the metrics are calculated by means of those last four quantities.
Conclusion
The results of the collective testing are shown in Table 1, where the bolded numbers correspond to the best outcomes for each metric. The PS-WASD definitely stands out as it scores the lowest MAE, the highest F-measure and Accuracy. In the departments of Recall and Precision it takes second place to the B-WASD and KNB, respectively. However, high performance at certain metrics does not seem to come at a cost of unjustifiably low scores on the rest of metrics, as is the case with the latter two models. Thus, the PS-WASD proves itself a reliable classifier that does not simply excel at one metric but rather performs exceptionally well all around.
In order to properly assess whether one can conclude to a model that is better suited for predicting credit card attrition in the specific dataset, we add to the previous analysis a statistical element, in the form of a mid-p-value McNemar test (Simos et al., 2022). The purpose of this test is to check whether two classifiers demonstrate equal accuracy (null hypothesis) or unequal accuracy (alternative hypothesis) in predicting the true class. We took all possible combinations of pairs consisting of the PS-WASD and one of the other four models and conducted the mid-p-value McNemar test. The results are shown in Table 2. At the 5% significance level, there is strong evidence to reject the null hypothesis for all pairs. The superior accuracy of the PS-WASD is thus put into firm ground.
To conclude, this paper introduced a PS-WASD neuronet in view of classifying credit card attrition. When applied to a publicly available credit card attrition dataset, the PS-WASD demonstrated either superior or highly competitive performance capabilities, compared to a number of well-established and well-performing classifiers. The credibility of those results is further supported by the conduction of a mid-p-value McNemar test through which we have been able to assert that the difference between the predictive accuracy of the PS-WASD and the rest of the models is in fact statistically significant. We may thus conclude that the PS-WASD classifier is a reliable classifier that can successfully take up the task of classifying credit card attrition.
Acknowledgments
This work was supported by the Ministry of Science and Higher Education of the Russian Federation (Grant No. 075-15-2022-1121).
References
Bigdeli, B., Pahlavani, P., & Amirkolaee, H. A. (2021). An ensemble deep learning method as data fusion system for remote sensing multisensor classification. Applied Soft Computing, 110, 107563. DOI:
Ed-daoudy, A., & Maalmi, K. (2020). Breast cancer classification with reduced feature set using association rules and support vector machine. Network Modeling Analysis in Health Informatics and Bioinformatics, 9(1), 34. DOI:
Esen, H., Esen, M., & Ozsolak, O. (2017). Modelling and experimental performance analysis of solar-assisted ground source heat pump system. Journal of Experimental & Theoretical Artificial Intelligence, 29(1), 1-17. DOI:
Esen, H., Ozgen, F., Esen, M., & Sengur, A. (2009). Artificial neural network and wavelet neural network approaches for modelling of a solar air heater. Expert Systems with Applications, 36(8), 11240-11248. DOI:
Farquad, M. A. H., Ravi, V., & Raju, S. B. (2014). Churn prediction using comprehensible support vector machine: An analytical CRM application. Applied Soft Computing, 19, 31-40. DOI:
García, D. L., Nebot, À., & Vellido, A. (2017). Intelligent data analysis approaches to churn as a business problem: a survey. Knowledge and Information Systems, 51(3), 719-774. DOI:
He, B., Shi, Y., Wan, Q., & Zhao, X. (2014). Prediction of Customer Attrition of Commercial Banks based on SVM Model. Procedia Computer Science, 31, 423-430. DOI:
Hu, X. (2005). A Data Mining Approach for Retailing Bank Customer Attrition Analysis. Applied Intelligence, 22(1), 47-60. DOI:
Huang, C., Jia, X., & Zhang, Z. (2018). A Modified Back Propagation Artificial Neural Network Model Based on Genetic Algorithm to Predict the Flow Behavior of 5754 Aluminum Alloy. Materials, 11(5), 855. DOI:
Mourtas, S. D., & Katsikis, V. N. (2022). Exploiting the Black-Litterman framework through error-correction neural networks. Neurocomputing, 498, 43-58. DOI:
Simos, T. E., Katsikis, V. N., & Mourtas, S. D. (2022). A multi-input with multi-function activated weights and structure determination neuronet for classification problems and applications in firm fraud and loan approval. Applied Soft Computing, 127, 109351. DOI:
Tang, L., Thomas, L., Fletcher, M., Pan, J., & Marshall, A. (2014). Assessing the impact of derived behavior information on customer attrition in the financial service industry. European Journal of Operational Research, 236(2), 624-633. DOI:
Zeng, T., Zhang, Y., Li, Z., Qiu, B., & Ye, C. (2020). Predictions of USA Presidential Parties From 2021 to 2037 Using Historical Data Through Square Wave-Activated WASD Neural Network. IEEE Access, 8, 56630-56640. DOI:
Zhang, Y., Chen, D., & Ye, C. (2019). Deep neural networks: wasd neuronet models, algorithms, and applications. CRC Press.
Copyright information

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License
About this article
Publication Date
27 February 2023
Article Doi
eBook ISBN
978-1-80296-960-3
Publisher
European Publisher
Volume
1
Print ISBN (optional)
-
Edition Number
1st Edition
Pages
1-403
Subjects
Hybrid methods, modeling and optimization, complex systems, mathematical models, data mining, computational intelligence
Cite this article as:
Mourtas, S. D., Katsikis, V. N., & Sahas, R. (2023). Credit Card Attrition Classification Through Neuronets. In P. Stanimorovic, A. A. Stupina, E. Semenkin, & I. V. Kovalev (Eds.), Hybrid Methods of Modeling and Optimization in Complex Systems, vol 1. European Proceedings of Computers and Technology (pp. 86-93). European Publisher. https://doi.org/10.15405/epct.23021.11

