Modeling of the Aggregator-Platform for Historical and Cultural Data "Siberiana"

Abstract

The purpose of this work is to create a model that would allow structuring complex humanitarian data and would allow scientists to process them. Modeling of a Siberian integrated system designed for storing and processing primary and research data. The requirements for the system for its further design are being formed. A relational database model based on UML notation is being created to store complex humanitarian primary and research data. A preliminary study revealed the need to separate user access using rules and API connections. A mathematical model of an integrated system of information objects is proposed, which provides identification and formalization of dependencies between objects and systems adequately describes the intersystem features of information systems. In the future, this can solve the problem of storing complex humanitarian data and providing multi-user access for the purpose of processing scientific information, as well as obtaining consistent integrated information using data exchange and updating mechanisms.

Keywords: Modelling the processes, processing of primary, cultural heritage of Siberia, information systems, databases

Introduction

One of the promising directions in modern interdisciplinary research is the application of mathematical modeling in history, cultural studies and other humanities.

At the same time, on the one hand, information about objects is often duplicated and not always relevant, which leads to its inconsistency and incompleteness. On the other hand, in order to support decision-making in the field of humanities, it becomes necessary to obtain results based on all the data collected and processed by various representatives. In addition to the direct task of obtaining integrated data, there is also an inverse task: data processing, which determines the need to change some information in different systems. The problem is to ensure the integrity of the entire data set (Haslhofer & Isaac, 2011).

There are various approaches to solving these problems. In the works of foreign and domestic authors, various ways of forming an integrated information environment are proposed: from creating systems based on a single data structure to using large data warehouses, as well as a universal business integration platform that would combine disparate technologies into a single product that would solve the problems of integrating humanitarian applications. It seems promising to approach server capacities, storage devices, desktop services and applications as universal resources.

Currently, primary and research data on the Yenisei Siberia are stored in a fragmented form. Scientists and researchers have to do a huge amount of work in order to work with this data. So, first you need to find out the storage location of the data you are interested in, which will most likely have to be done over the phone, then find a responsible person who can give permission to work with the data and then visit the data storage location. It is also worth mentioning that Siberia is the subject of interest of many world scientists, for whom visiting our region is a difficult task. Due to the difficulty of online access to the data of the Yenisei Siberia for further analysis, it became necessary to create an aggregate (digital library, platform). The next thing that prompted us to develop this system is that a huge amount of significant research is really being carried out in Yenisei Siberia and there is a need to preserve information about them and present it to the general public. But any modern information system (further IS) that stores encyclopedic data and is aimed at the work of a researcher in it is not just a functional structure, all elements of which must be organically interconnected and complement each other, but it is also the possibility of data processing.

One of the key tasks in the creation of the platform is the modeling of the Siberianа platform at all stages of development. The article discusses the stages of modeling data storage. With the spread of the Internet, the increase in computer power, the development of e-commerce, the "Internet of things" and other areas of human life accompanying (de Boer et al., 2012).

The "information society" or "knowledge society", the demand for research in this direction is increasing, as well as the areas of application of digital humanities are expanding, which, most likely, will lead in the coming decades to increase the number of studies and the amount of funds allocated for the development of Digital Humanities (Hyvönen, 2012).

Problem Statement

The platform is designed for convenient and multifunctional access, provided by the integration of services (search, analytical, instrumental), to materials collected and digitized in the framework of archaeological research, manuscripts and book monuments, natural heritage items and other digital resources that reflect a special territorial, economic and cultural - the historical significance of the Yenisei Siberia for a wide audience (representatives of the academic community, the general public, freelance teams, volunteers, amateur experts, "new" local historians, etc.). Based on this, general requirements for the IS "Siberiana" were presented, presented in Table 1.

The main function of the information system "Siberiana" is a true reflection of the research data stored on the territory of the Yenisei Siberia, reflecting the historical and cultural heritage of the region and allowing to work with data (Isaac & Haslhofer, 2013). Siberiana will allow you to move away from the inaccessibility of data, eliminate gaps, create a complete picture and provide intelligent work with data, that is the tasks of IS are the effective storage, processing and analysis of data. To do this, the IS should present the characteristics presented in Table 2.

At the same time, the IS should provide users with access to analytical information protected from unauthorized use. Protecting data from unauthorized access is one of the priority tasks in the design of any IS (Manovich, 2000).

Increasingly high requirements are imposed on ensuring the reliability of data, so relational database management systems have become the dominant tool in this area. The use of other models does not increase the efficiency of developing recommendations and solutions but complicates the IS architecture. A relational database model that meets all the above requirements is shown in Figure 1 (Manovich, 1999).

See Full Size >

Research Questions

Modelling of a modern information system that stores encyclopaedic data and aims at the researcher's work in it is a functional structure, all elements of which should be organically interconnected and complement each other, but this is also the possibility of data processing.

Purpose of the Study

Designing the user's work with historical and cultural information and making a division into roles in order to expand the possibilities of working in the researcher's system and preserve access for an ordinary user. To solve the problem of the lack of ready-made models of scientific work with humanitarian data on a computer. Visualize the model in order to reduce the complexity of system development, reduce the number of possible errors and reduce the overall development time. To identify the influence and dependencies of various criteria on the final result of the work (Manovich, 2012).

Research Methods

Modelling the System (Structure)

Working with humanitarian data is complex and ambiguous. To begin with, we presented it in a simplified form, but with a mention of all the necessary components for normal functioning (Antamoshkin et al., 2022). The structure of the functioning of the information system is shown in Figure 2.

To integrate data at the logical level, each data user must have a role that provides the necessary access to data, support for standard Internet protocols, conversion of standard queries into queries in an internal data format, and delivery of query results to the end user.

See Full Size >

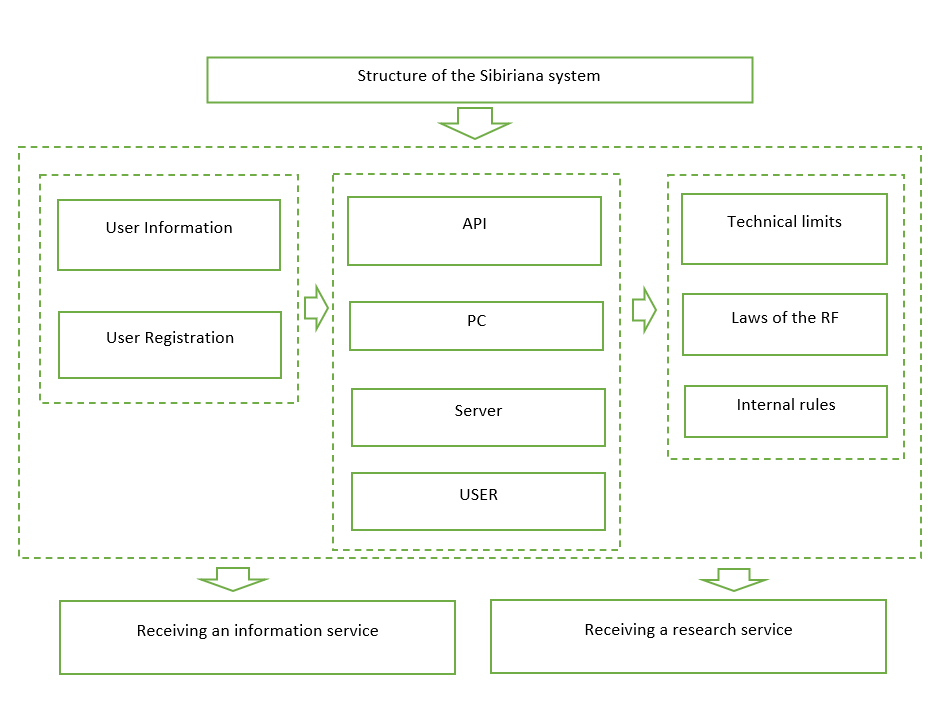
Siberiana works with the user, so the functioning technology is divided into 5 main stages: authorization, search query, information filtering, information processing and uploading processing results. At the authorization stage, the user enters the system and registers in it, or is authorized if already registered. He enters the standard data for registration into the specified fields: name, email, phone number and agrees to the processing of data. But also, in the system at the modeling stage, it was revealed that during registration it was necessary to enter such fields as the user's role and the presence of personal collections. These fields will subsequently provide security for data storage and deep work on them (Kravchenko et al., 2020).

Representation of the Algorithm of User Interaction in the System

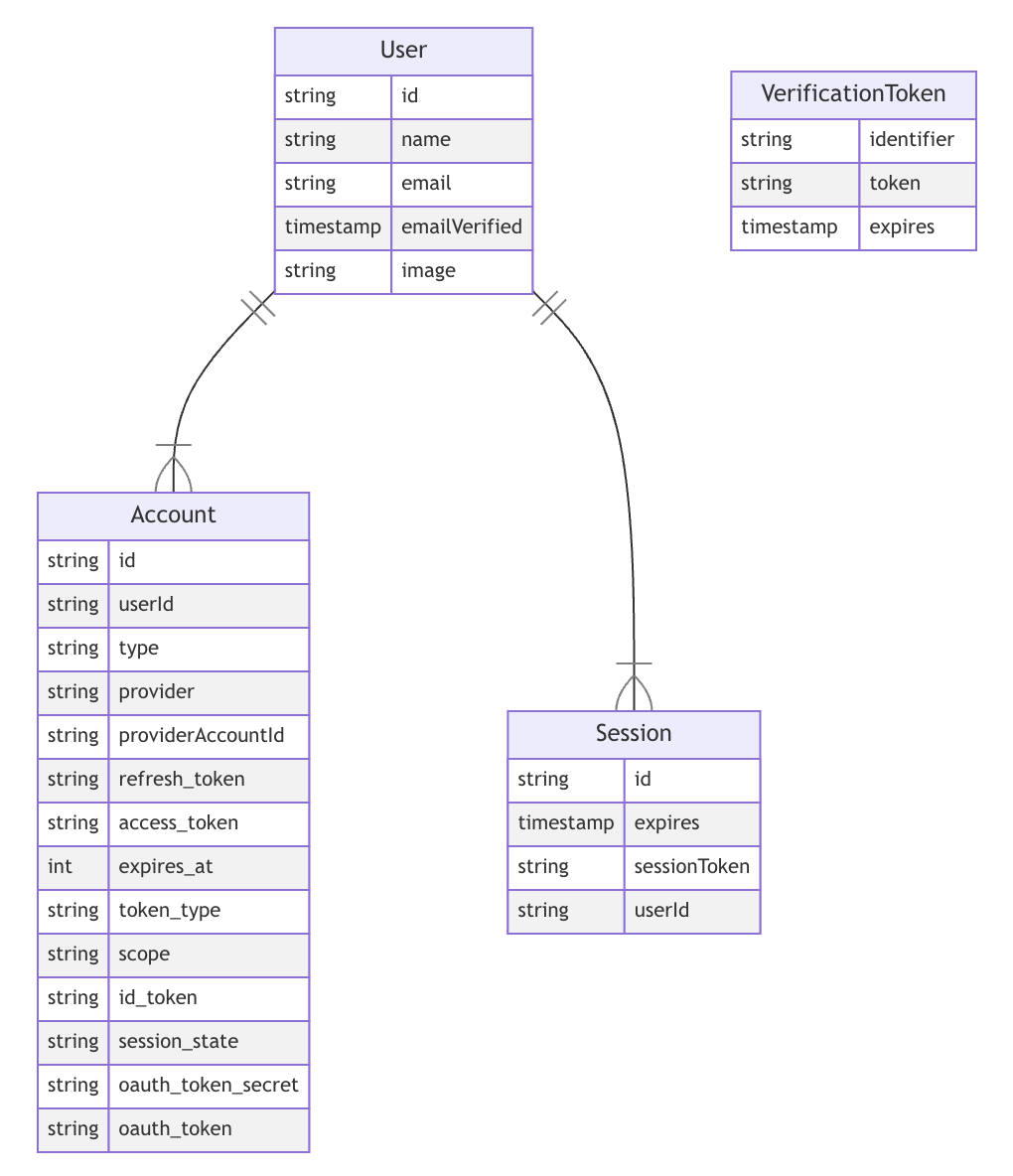
The library is used to authenticate users NextAuth.js. It is necessary to implement an approximate structure that NextAuth.js expects from the database shown in Figure 3.

See Full Size >

After authorization, the user starts working in the system - sets a search query. For example, porcelain bowls. At the next stage, the user filters the found objects by administrative location, site of the monument, dating of the object, its relation to the collection, etc.

When the material is found and filtered, the user can start processing information if he is a researcher. For example, count all the porcelain bowls found in the Lower Angara region since 2000. Based on these data, build a graphical representation of the processing results.

Providing the Integration Function

After conducting a thorough study and modeling of some parts of the IP, we proposed a data integration model that allows us to analyze intersystem connections, dependencies and patterns that arise between information objects (Tynchenko et al., 2021). The analysis of the problem domain, modeling goals, as well as the discrete nature of the modeling object indicated the possibility of using a high-level abstraction of the set-theoretic apparatus for constructing a mathematical model of data integration. The basic concept of the proposed model is the concept of an information object (IO). As a rule, objects correspond to the entities of the subject area, each object is characterized by the values of a given set of attributes. Therefore, an information object is defined as a set of ordered pairs of the form:

$\mathrm{x}=\left\{<{\mathrm{a}}_1\mathrm{}{\mathrm{d}}_{\mathrm{1}\mathrm{}}>,\mathrm{}<{\mathrm{a}}_2\mathrm{}{\mathrm{d}}_2>,\mathrm{}\dots ,<{\mathrm{a}}_{\mathrm{n}}\mathrm{}{\mathrm{d}}_{\mathrm{n}}>\right\},\mathrm{}{\mathrm{a}}_{\mathrm{i}}\ne {\mathrm{a}}_{\mathrm{j}},\mathrm{}\mathrm{i}\mathrm{}\ne \mathrm{}\mathrm{j},\mathrm{}\mathrm{i},\mathrm{}\mathrm{j}\mathrm{}\in \mathrm{}[\mathrm{1}...\mathrm{n}]$

where a – name attribute, d – attribute value.

Under the information system, we will consider some information scheme describing the characteristics of the objects included in the system, and a set of IO satisfying this scheme.

The information schema (IS) a tuple $S\mathrm{}=<\mathrm{}A,D,T,\varphi ,\delta \mathrm{}>$ , where $A\mathrm{}=\{a_{\mathrm{1}},a_{\mathrm{2}},\dots ,\mathrm{}{a}_k\}$ – is a set of attributes of information objects; $D\mathrm{}=\{D_{\mathrm{1}},\mathrm{}{D}_{\mathrm{2}},\dots ,\mathrm{}{D}_m\}$ – is a family of sets of possible attribute values; $T\mathrm{}=\mathrm{}{t}_{\mathrm{1}},\mathrm{}{t}_{\mathrm{2}},\dots ,\mathrm{}{t}_l\}$ – is a set of object types; $\varphi \mathrm{}:\mathrm{}A\mathrm{}\to \mathrm{}D$ is a mapping that matches each attribute with a set of its possible values; $\delta \mathrm{}:T\mathrm{}\to \mathrm{}{\mathrm{2}}^A$ – is a mapping specifying for each type a set of attributes of its elements.

The information system (IS) built according to the scheme S, we will call the tuple $Uˢ=<\mathrm{}S,U\mathrm{},\gamma >$, where $S\mathrm{}=<\mathrm{}A,\mathrm{}D,T\mathrm{},\varphi ,\delta \mathrm{}>$ – information scheme. $U\mathrm{}=\mathrm{}\{x_{\mathrm{1}},\mathrm{}{x}_{\mathrm{2}},...,\mathrm{}{x}_n\}$ – set of information objects; $\gamma \mathrm{}:U\mathrm{}\to \mathrm{}T$ – a mapping that matches the object with its type, and for any information object $x\in U$ the conditions are met:

• the set of attributes corresponds to the type {a:<a,d>∈x}=δ(γ(x));
• for any pair <a,d>∈x we have d∈ϕ(a).

The change of IS is set by the mapping $F:Wˢ\to Wˢ$ , where $Wˢ$ – a lot of all information systems satisfying scheme $S$.

Let's define a set of information systems $U\mathrm{ˢ}\mathrm{}=\mathrm{}\{U_{\mathrm{1}}\mathrm{ˢ},\mathrm{}{U}_{\mathrm{2}}\mathrm{ˢ}\mathrm{},...,U_n\mathrm{ˢ}\mathrm{}\}$, where $U_n\mathrm{ˢ}=<\mathrm{}{S}_i,U_i,{\gamma }_i\mathrm{}>$ and $S\mathrm{}=<\mathrm{}{A}_i,\mathrm{}{D}_i,T_i,{\varphi }_i,{\delta }_i>$, and we introduce the notation:

$S\mathrm{}=\mathrm{}\left\{S_{\mathrm{1}},\mathrm{}{S}_{\mathrm{2}},\dots ,\mathrm{}{S}_n\right\},\mathrm{}A=Y{A}_I,\mathrm{}D=Y{D}_I,\mathrm{}T=Y{T}_i,\mathrm{}U=Y{U}_i$

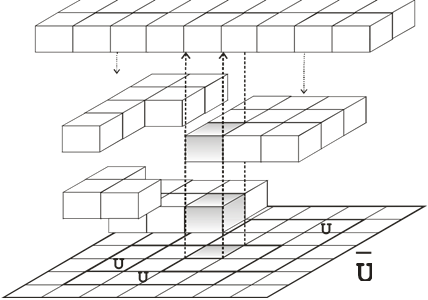
Based on this, we have built a model that can serve as a basis for specifying semantic dependencies and applying data integration technology in the chosen subject area. The model is shown in Figure 4.

See Full Size >

Findings

Adequately describes the intersystem features of information systems. The mathematical model of the integrated system of accounting of information objects is constructed, which allows to identify and formalize dependencies between objects and systems.

When developing models of the database and the information system "Siberiana" we designed the user's ambiguous work with historical and cultural information and made a division into roles, which made it possible to expand the possibilities of working in the researcher's system and save access for the ordinary user. One of the main problems in this area is that there are no ready-made models for describing humanitarian data. Create of models can significantly reduce the complexity of system development, reduce the number of possible errors and reduce the overall development time. Simulation of the Siberian system helped to identify the influence and dependencies of various criteria on the final result of the work.

Conclusion

At the next stage of modeling, we plan to lower the level of abstraction of the model, to allocate the main classes of objects of the unified information space, for which the structure is determined: properties, behavior and mutual relation. To build a multi-level object scheme of an integrated system in which the base class for accounting objects is the "Information Object" class (main elements: key attributes, state and methods that change the state).

The mathematical model of the integrated system of accounting of information objects is constructed, which allows to identify and formalize dependencies between objects and systems.

When developing models of the database and the information system "Siberiana" we designed the user's ambiguous work with historical and cultural information and made a division into roles, which made it possible to expand the possibilities of working in the researcher's system and save access for the ordinary user. One of the main problems in this area is that there are no ready-made models for describing humanitarian data. Create of models can significantly reduce the complexity of system development, reduce the number of possible errors and reduce the overall development time. Simulation of the Siberiana system helped to identify the influence and dependencies of various criteria on the final result of the work.

References

• Antamoshkin, O. A., Antamoshkina, O. A., Bryukhanova, E. R., Stupin, A. O., & Kamenskaya, N. V. (2022). Methodology for automated classification of farmland based on Earth remote sensing data. IOP Conference Series: Earth and Environmental Science, 981(3), 032015. DOI:

  Google Scholar

  Crossref

• de Boer, V., Wielemaker, J., van Gent, J., Hildebrand, M., Isaac, A., van Ossenbruggen, J., & Schreiber, G. (2012). Supporting Linked Data Production for Cultural Heritage Institutes: The Amsterdam Museum Case Study. Lecture Notes in Computer Science, 7295, 733-747. DOI:

  Google Scholar

  Crossref

• Haslhofer, B., & Isaac, A. (2011). data. europeana. eu: The europeana linked open data pilot. In International Conference on Dublin Core and Metadata Applications (pp. 94-104).

• Hyvönen, E. (2012). Publishing and Using Cultural Heritage Linked Data on the Semantic Web. Synthesis Lectures on the Semantic Web: Theory and Technology, 2(1), 1-159. DOI:

  Google Scholar

  Crossref

• Isaac, A., & Haslhofer, B. (2013). Europeana Linked Open Data - data.europeana.eu. Semantic Web, 4(3), 291-297. DOI:

  Google Scholar

  Crossref

• Kravchenko, A. V., Dragunova, E. V., & Kirillov, Y. V. (2020). Modeling business processes: textbook. Novosibirsk State Technical University, 31-32.

• Manovich, L. (1999). Database as Symbolic Form. Convergence: The International Journal of Research into New Media Technologies, 5(2), 80-99. DOI:

  Google Scholar

  Crossref

• Manovich, L. (2000). Database as a genre of new media. AI & Society, 14(2), 176-183. DOI:

  Google Scholar

  Crossref

• Manovich, L. (2012). How to compare one million images? In D. M. Berry (Ed.), Understanding digital humanities (pp. 249-278). Palgrave Macmillan. DOI:

  Google Scholar

  Crossref

• Tynchenko, V. S., Lukovenko, A. S., Kukartsev, V. V., Antamoshkin, O. A., Tynchenko, S. V., Sergienko, R. B., Mikhalev, A. S., & Panfilov, I. A. (2021). System Diagnostics of Supporting-Rod Porcelain Insulation at Digital Substations. WSEAS Transactions On Power Systems, 16, 195-203. DOI:

  Google Scholar

  Crossref